find the solution (√(x^2 −3x−4 ))


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 82191 by jagoll last updated on 19/Feb/20

$f i n d t h e s o l u t i o n$ $\sqrt{x^{2} - 3 x - 4} > x - 2$
Commented byarkanmath7@gmail.com last updated on 19/Feb/20
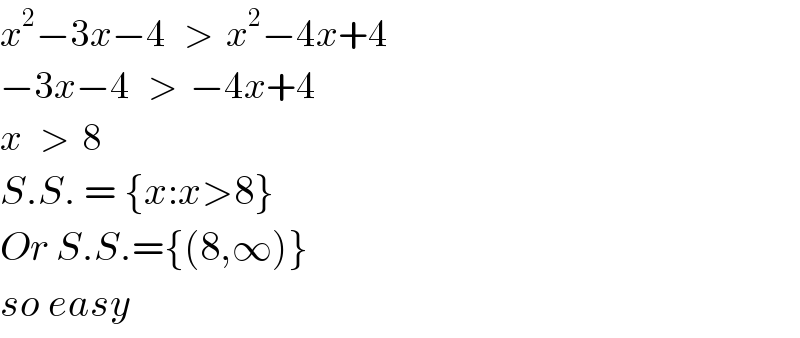
$x^2 −3x−4 > x^2 −4x+4 −3x−4 > −4x+4 x > 8 S.S. = {x:x>8} Or S.S.={(8,∞)} so easy$
$x^{2} - 3 x - 4 > x^{2} - 4 x + 4$ $- 3 x - 4 > - 4 x + 4$ $x > 8$ $S . S . = {x : x > 8}$ $O r S . S . = {(8, \infty)}$ $s o e a s y$
Commented byjagoll last updated on 19/Feb/20

$t e s f o r x = - 1$ $\sqrt{1 + 3 - 4} > - 3$ $0 > - 3 i s c o r r e c t s i r$
Commented byjagoll last updated on 19/Feb/20

$x = - 1 \notin (8, \infty) b u t x = - 1 i s s o l u t i o n$
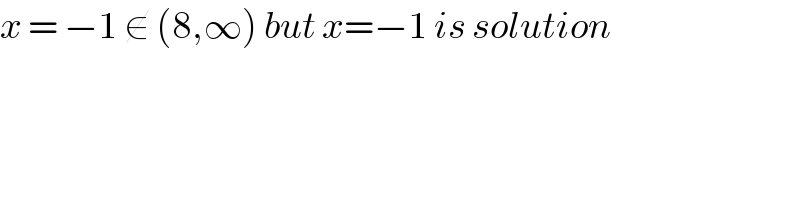
Commented bymr W last updated on 19/Feb/20

$\sqrt{(x - 4) (x + 1)} > x - 2$ $s o l u t i o n :$ $x ⩽ - 1 \lor x > 8$
Commented byarkanmath7@gmail.com last updated on 19/Feb/20

$I t h i n k {t h a t}^{'} s t r u e i f y o u s a i d \sqrt{x^{2} - 3 x - 4} ⩾ 0$ $n o t w h e n \sqrt{x^{2} - 3 x - 4} > x - 2$ $p u t x = - 1 i n t h e 2 n d l i n e o f t h e s o l u t i o n$ $y o u w i l l g e t a r o n g s t a t e m e n t$
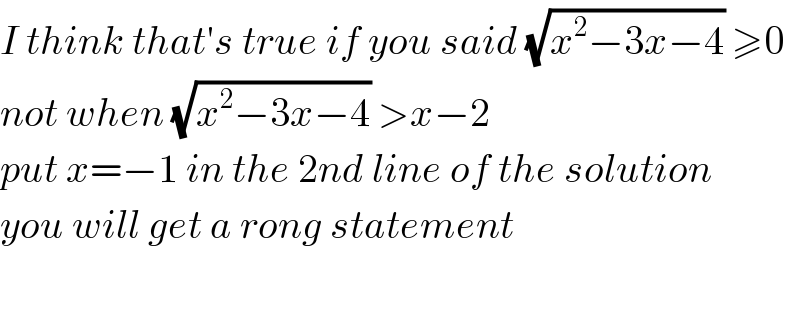
Commented byKunal12588 last updated on 19/Feb/20

$x > 8$ $a n d \sqrt{(x + 1) (x - 4)} > (x - 2)$ $\Rightarrow \frac{(x + 1) (x - 4)}{{(x - 2)}^{2}} > 0$ $\Rightarrow x < - 1$
Commented bymr W last updated on 19/Feb/20

$w h y u s e i f \sqrt{x^{2} - 3 x - 4} ⩾ 0 ? i t i s a l w a y s$ $t r u e t h a t \sqrt{x^{2} - 3 x - 4} ⩾ 0 .$
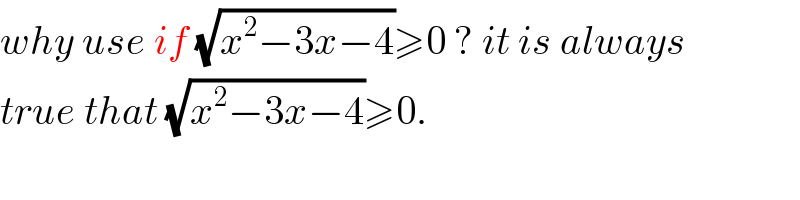
Commented byjagoll last updated on 19/Feb/20

$s o w h a t i s t h e a n s w e r c o n c l u s i o n ?$ $x ⩽ - 1 \lor x > 8$ $o r x > 8 ?$
Commented bymr W last updated on 19/Feb/20

$w h e n x ⩽ - 1, x - 2 ⩽ - 3, b u t$ $\sqrt{x^{2} - 3 x - 4} ⩾ 0, t h e r e f o r e$ $\sqrt{x^{2} - 3 x - 4} > x - 2 i s t r u e . a n d x = - 1$ $i s a l s o i n c l u d e d .$
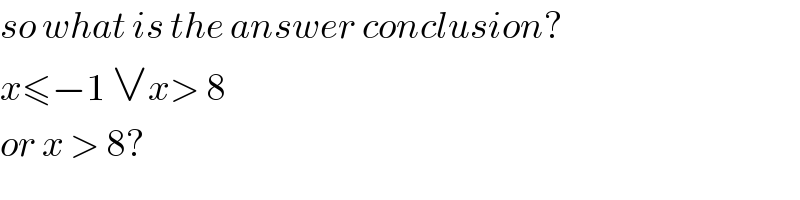
Commented bymr W last updated on 19/Feb/20

$t h e r e s u l t i s$ $x ⩽ - 1 \lor x > 8$ $t h a t m e a n s x \in (- \infty, - 1] o r x \in (8, + \infty)$
Commented byjagoll last updated on 19/Feb/20

$y e s s i r . i a g r e e . b u t m y t e a c h e r$ $b l a m e d m y a n s w e r$
Commented byarkanmath7@gmail.com last updated on 19/Feb/20

$c o n f u s e d q u e s t$ $i t h i n k y o u a r e t h e t r u e s t$
Commented byjagoll last updated on 19/Feb/20

$h a h a . . . i f t h e m o s t c o r r e c t,$ $s u r e l y G o d s i r$
Commented bymr W last updated on 19/Feb/20

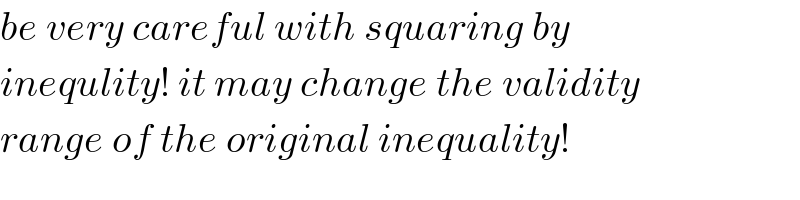
$b e v e r y c a r e f u l w i t h s q u a r i n g b y$ $i n e q u l i t y! i t m a y c h a n g e t h e v a l i d i t y$ $r a n g e o f t h e o r i g i n a l i n e q u a l i t y!$
Commented byjagoll last updated on 19/Feb/20

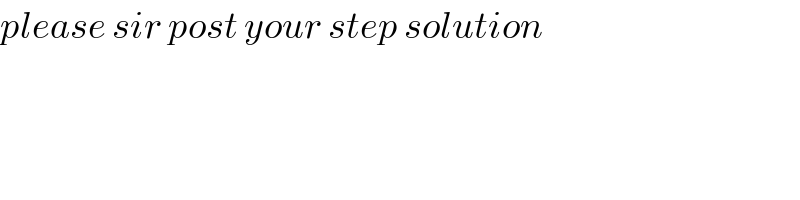
$p l e a s e s i r p o s t y o u r s t e p s o l u t i o n$
Commented byjagoll last updated on 19/Feb/20

Commented byjagoll last updated on 19/Feb/20

$i t s i r b y g r a p h i c$
Commented bymathmax by abdo last updated on 19/Feb/20

$t h e i n e q u a t i o n i s d e f i n e d f o r x ⩾ 2 a n d x^{2} - 3 x - 4 ⩾ 0$ $Δ = {(- 3)}^{2} - 4 (- 4) = 9 + 16 = 25 \Rightarrow x_{1} = \frac{3 + 5}{2} = 4 a n d x_{2} = \frac{3 - 5}{2} = - 1$ $x^{2} - 3 x - 4 ⩾ 0 \Rightarrow x \in] - \infty, - 1 [\cup] 4, + \infty [\Rightarrow D_{i n} = [2, + \infty [$ $(i n) \Rightarrow x^{2} - 3 x - 4 > x^{2} - 4 x + 4 \Rightarrow x > 8 \Rightarrow S = [8, + \infty [$
Commented byjagoll last updated on 19/Feb/20

$s o l u t i o n x ⩽ - 1 \lor x > 8$
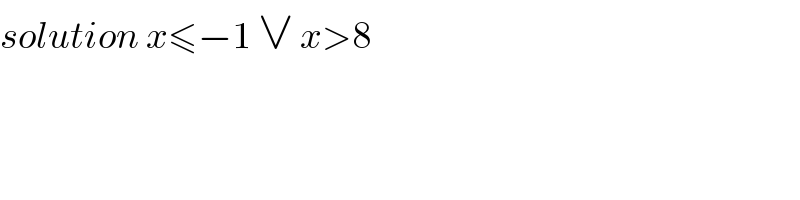
	Answered by mr W last updated on 19/Feb/20

	$s u c h t h a t \sqrt{x^{2} - 3 x - 4} i s d e f i n e d,$ $x^{2} - 3 x - 4 = (x + 1) (x - 4) ⩾ 0$ $\Rightarrow x ⩽ - 1 o r x ⩾ 4$ $c a s e 1 : x ⩽ - 1$ $w i t h x ⩽ - 1, w e h a v e x - 2 ⩽ - 3 < 0$ $b u t \sqrt{x^{2} - 3 x - 4} ⩾ 0, s o$ $\sqrt{x^{2} - 3 x - 4} > x - 2 i s t r u e .$ $\Rightarrow x ⩽ - 1 i s s o l u t i o n .$ $c a s e 2 : x ⩾ 4$ $w i t h x ⩾ 4, x - 2 ⩾ 6 > 0$ $x^{2} - 3 x - 4 > {(x - 2)}^{2}$ $x^{2} - 3 x - 4 > x^{2} - 4 x + 4$ $x > 8 ⩾ 4$ $\Rightarrow x > 8 i s s o l u t i o n .$ $(w e c a n u s e s q u a r i n g h e r e b e c a u s e w e$ $h a v e e n s u r e d a t f i r s t t h a t x - 2 > 0)$ $s u m m a r y o f a l l s o l u t i o n s :$ $x ⩽ - 1$ $x > 8$
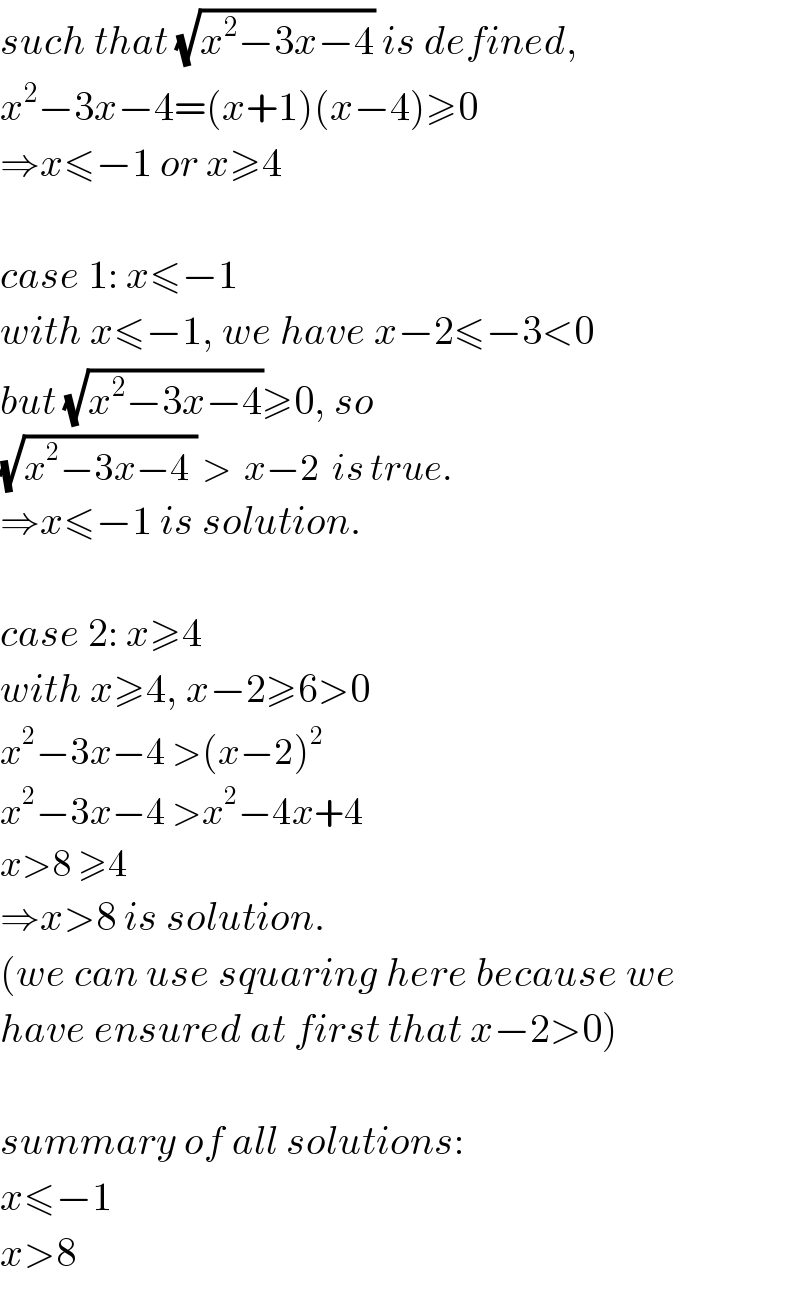
	Commented byjagoll last updated on 19/Feb/20

	$t h a n k y o u s i r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum