Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 8224 by trapti rathaur@ gmail.com last updated on 03/Oct/16

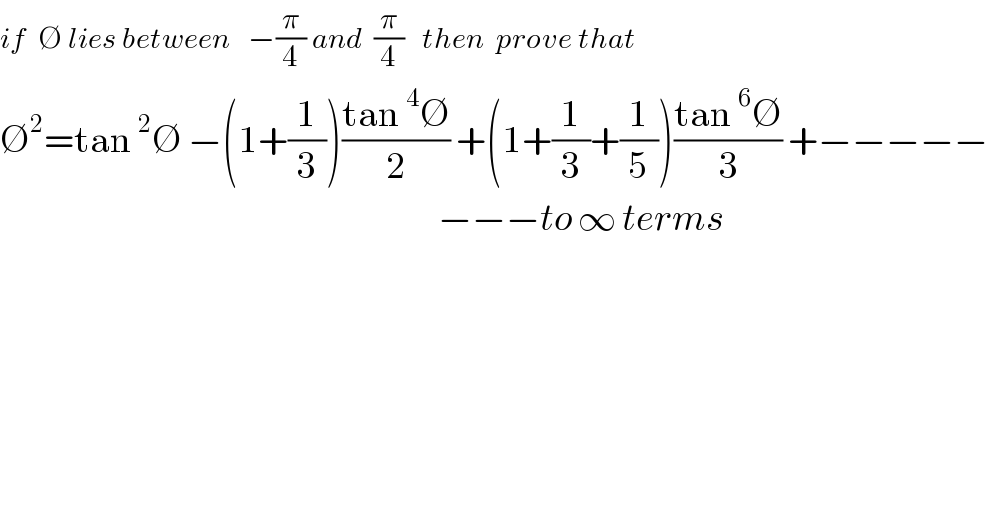
if ∅ lies between −(π/4) and (π/4) then prove that ∅^2 =tan^2 ∅ −(1+(1/3))((tan^4 ∅)/2) +(1+(1/3)+(1/5))((tan^6 ∅)/3) +−−−−− −−−to ∞ terms

$${if}\:\:\varnothing\:{lies}\:{between}\:\:\:−\frac{\pi}{\mathrm{4}}\:{and}\:\:\frac{\pi}{\mathrm{4}}\:\:\:{then}\:\:{prove}\:{that} \\ $$$$\varnothing^{\mathrm{2}} =\mathrm{tan}\:^{\mathrm{2}} \varnothing\:−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)\frac{\mathrm{tan}\:^{\mathrm{4}} \varnothing}{\mathrm{2}}\:+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}\right)\frac{\mathrm{tan}\:^{\mathrm{6}} \varnothing}{\mathrm{3}}\:+−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−{to}\:\infty\:{terms} \\ $$$$ \\ $$

Commented by Yozzias last updated on 03/Oct/16

RTP: If b∈(((−π)/4),(π/4))⇒b^2 =Σ_(r=1) ^∞ (−1)^(r−1) (1/r){Σ_(k=1) ^r (1/(2k−1))}tan^(2r) b. or b^2 =lim_(n→∞) [Σ_(r=1) ^n (−1)^(r−1) (1/r){Σ_(k=1) ^r (1/(2k−1))}tan^(2r) b]

$$\mathrm{RTP}:\:\mathrm{If}\:\mathrm{b}\in\left(\frac{−\pi}{\mathrm{4}},\frac{\pi}{\mathrm{4}}\right)\Rightarrow\mathrm{b}^{\mathrm{2}} =\underset{\mathrm{r}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{r}−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{r}}\left\{\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{r}} {\sum}}\frac{\mathrm{1}}{\mathrm{2k}−\mathrm{1}}\right\}\mathrm{tan}^{\mathrm{2r}} \mathrm{b}. \\ $$$$\mathrm{or}\:\mathrm{b}^{\mathrm{2}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{r}−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{r}}\left\{\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{r}} {\sum}}\frac{\mathrm{1}}{\mathrm{2k}−\mathrm{1}}\right\}\mathrm{tan}^{\mathrm{2r}} \mathrm{b}\right] \\ $$$$ \\ $$

Commented by trapti rathaur@ gmail.com last updated on 03/Oct/16

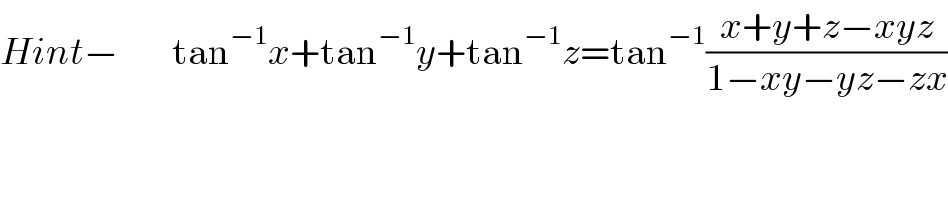
Hint− tan^(−1) x+tan^(−1) y+tan^(−1) z=tan^(−1) ((x+y+z−xyz)/(1−xy−yz−zx))

$${Hint}−\:\:\:\:\:\:\:\:\:\mathrm{tan}^{−\mathrm{1}} {x}+\mathrm{tan}^{−\mathrm{1}} {y}+\mathrm{tan}^{−\mathrm{1}} {z}=\mathrm{tan}^{−\mathrm{1}} \frac{{x}+{y}+{z}−{xyz}}{\mathrm{1}−{xy}−{yz}−{zx}} \\ $$

Commented by trapti rathaur@ gmail.com last updated on 03/Oct/16

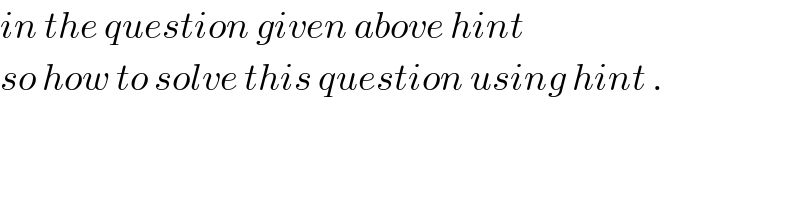
in the question given above hint so how to solve this question using hint .

$${in}\:{the}\:{question}\:{given}\:{above}\:{hint} \\ $$$${so}\:{how}\:{to}\:{solve}\:{this}\:{question}\:{using}\:{hint}\:. \\ $$

Answered by prakash jain last updated on 03/Oct/16

Taylor series expansion for tan^(−1) x tan^(−1) x=x−(x^3 /3)+(x^5 /5)+−... (for −1<x<1) (tan^(−1) x)^2 =(x−(x^3 /3)+(x^5 /5)−+...)(x−(x^3 /3)+(x^5 /5)−+...) when n is even coefficient of x^n is obtained by multiplying coeeficients for example coefficient of x^6 =a_1 a_5 +a_3 a_3 +a_5 a_1 where a_n is coeffiient of x^n in tan^(−1) x c_n =coefficient of x^n = { ((Σ_(k=1) ^(n/2) (1/((2k−1)(2(n−k)+1)))),(n even)),(0,(n odd)) :} Σ_(k=1) ^(n/2) (1/((2k−1)(2(n−k)+1))) =Σ_(k=1) ^(n/2) (1/n)((1/(2k−1))+(1/(2((n/2)−k)+1))) =(1/n)(Σ_(k=1) ^(n/2) (1/(2k−1))+Σ_(k=1) ^(n/2) (1/(2((n/2)−k)+1))) =(1/n)(Σ_(k=1) ^(n/2) (1/(2k−1))+Σ_(k=1) ^(n/2) (1/(2k−1))) c_2 =(2/n)Σ_(k=1) ^(n/2) (1/(2k−1)) c_n = { (((2/n)Σ_(k=1) ^(n/2) (1/(2k−1))),(n even)),(0,(n odd)) :} put x=tan ∅ (−(π/4)<∅<(π/4)) to get the required result

$$\mathrm{Taylor}\:\mathrm{series}\:\mathrm{expansion}\:\mathrm{for}\:\mathrm{tan}^{−\mathrm{1}} {x} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}+−...\:\left(\mathrm{for}\:−\mathrm{1}<{x}<\mathrm{1}\right) \\ $$$$\left(\mathrm{tan}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} =\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−+...\right)\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}}−+...\right) \\ $$$${when}\:{n}\:{is}\:{even}\:{coefficient}\:{of}\:{x}^{{n}} \:{is}\:{obtained} \\ $$$${by}\:{multiplying}\:{coeeficients} \\ $$$${for}\:{example}\:{coefficient}\:{of}\:{x}^{\mathrm{6}} ={a}_{\mathrm{1}} {a}_{\mathrm{5}} +{a}_{\mathrm{3}} {a}_{\mathrm{3}} +{a}_{\mathrm{5}} {a}_{\mathrm{1}} \: \\ $$$$\:\:\:\:\:\:{where}\:{a}_{{n}} \:{is}\:{coeffiient}\:{of}\:{x}^{{n}} {in}\:\mathrm{tan}^{−\mathrm{1}} {x} \\ $$$${c}_{{n}} =\mathrm{coefficient}\:\mathrm{of}\:{x}^{{n}} =\begin{cases}{\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}\left({n}−{k}\right)+\mathrm{1}\right)}}&{{n}\:{even}}\\{\mathrm{0}}&{{n}\:{odd}}\end{cases}\: \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}\left({n}−{k}\right)+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:=\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\frac{\mathrm{1}}{{n}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}\left(\frac{{n}}{\mathrm{2}}−{k}\right)+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{{n}}\left(\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}+\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}\left(\frac{{n}}{\mathrm{2}}−{k}\right)+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{{n}}\left(\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}+\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\right) \\ $$$${c}_{\mathrm{2}} =\frac{\mathrm{2}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}} \\ $$$${c}_{{n}} =\begin{cases}{\frac{\mathrm{2}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}}&{{n}\:{even}}\\{\mathrm{0}}&{{n}\:{odd}}\end{cases} \\ $$$$\mathrm{put} \\ $$$${x}=\mathrm{tan}\:\varnothing\:\left(−\frac{\pi}{\mathrm{4}}<\varnothing<\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{required}\:\mathrm{result} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com