
Question and Answers Forum
Question Number 82390 by jagoll last updated on 21/Feb/20
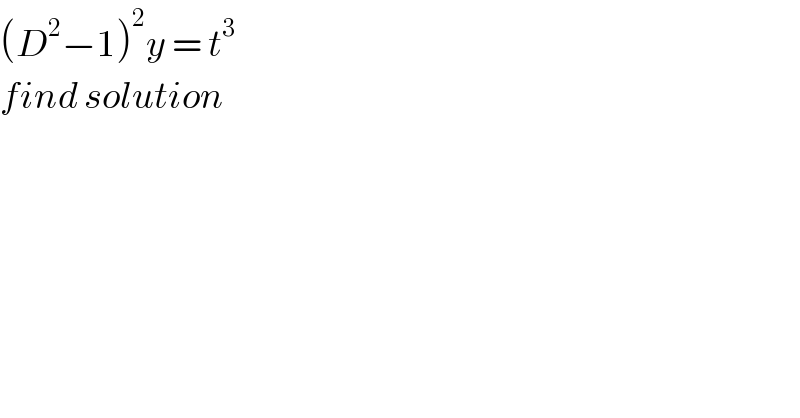
Answered by TANMAY PANACEA last updated on 21/Feb/20
![y=e^(mt) so (dy/dt)=me^(mt) and (d^2 y/dt^2 )=m^2 e^(mt) (m^2 −1)^2 =0 m=1,1,−1,−1 complementary function y=Ae^t +Bte^t +Ce^(−t) +Fte^(−t) particular intregal now formula (1+x)^(−2) =1−2x+3x^2 −4x^3 +... y=(t^3 /((D^2 −1)^2 ))=(t^3 /((1−D^2 )^2 )) y=(1−D^2 )^(−2) t^3 =(1+2D^2 +3D^4 +others terms ignored)t^3 =(t^3 +2×3×2t) [(dt^3 /dt)=3t^2 →((d(3t^2 ))/dt)=6t] =t^3 +12t complete solution y=Ae^t +Bte^t +Ce^(−t) +Fte^(−t) +t^3 +12t](Q82394.png)
Commented by jagoll last updated on 21/Feb/20

Commented by TANMAY PANACEA last updated on 21/Feb/20

| ||
Question and Answers Forum | ||
Question Number 82390 by jagoll last updated on 21/Feb/20 | ||
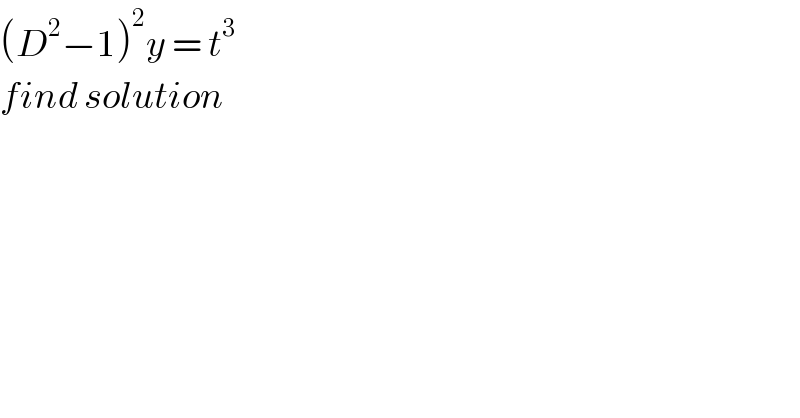 | ||
Answered by TANMAY PANACEA last updated on 21/Feb/20 | ||
![y=e^(mt) so (dy/dt)=me^(mt) and (d^2 y/dt^2 )=m^2 e^(mt) (m^2 −1)^2 =0 m=1,1,−1,−1 complementary function y=Ae^t +Bte^t +Ce^(−t) +Fte^(−t) particular intregal now formula (1+x)^(−2) =1−2x+3x^2 −4x^3 +... y=(t^3 /((D^2 −1)^2 ))=(t^3 /((1−D^2 )^2 )) y=(1−D^2 )^(−2) t^3 =(1+2D^2 +3D^4 +others terms ignored)t^3 =(t^3 +2×3×2t) [(dt^3 /dt)=3t^2 →((d(3t^2 ))/dt)=6t] =t^3 +12t complete solution y=Ae^t +Bte^t +Ce^(−t) +Fte^(−t) +t^3 +12t](Q82394.png) | ||
| ||
Commented by jagoll last updated on 21/Feb/20 | ||
 | ||
Commented by TANMAY PANACEA last updated on 21/Feb/20 | ||
 | ||