
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 82445 by mathmax by abdo last updated on 21/Feb/20
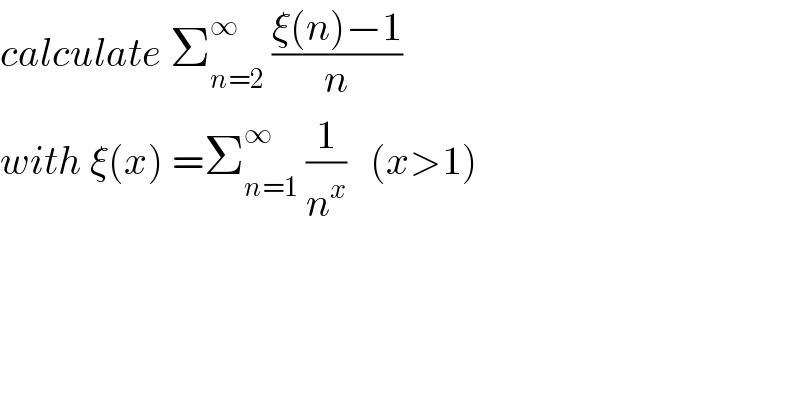
Answered by mind is power last updated on 21/Feb/20
![=Σ_(n≥2) (1/n).Σ_(m≥2) (1/m^n )=Σ_(m≥2) .Σ_(n≥2) (1/n).((1/m))^n =Σ_(m≥2) .[−ln(1−(1/m))−(1/m)] =Σ_(m≥2) [−ln(m−1)+ln(m)−(1/m)] =lim_(x→∞) .Σ_(m=2) ^x −ln(m−1)+ln(m)−(1/m)] =lim_(x→∞) ln(x)−Σ_(m=2) ^x (1/m) =−lim_(x→∞) {Σ_(m=2) ^x (1/m)−ln(x)} =−lim_(x→∞) {Σ_(m=1) ^x (1/m)−ln(x)−1}=−{γ−1}=1−γ γ Euler mechorini constent](Q82478.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 82445 by mathmax by abdo last updated on 21/Feb/20 | ||
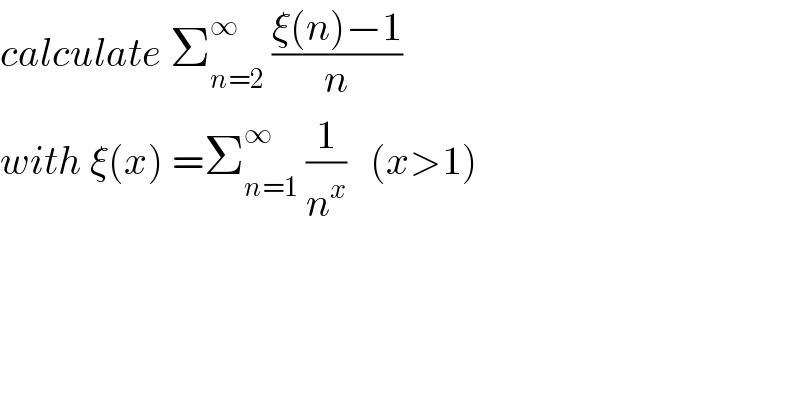 | ||
Answered by mind is power last updated on 21/Feb/20 | ||
![=Σ_(n≥2) (1/n).Σ_(m≥2) (1/m^n )=Σ_(m≥2) .Σ_(n≥2) (1/n).((1/m))^n =Σ_(m≥2) .[−ln(1−(1/m))−(1/m)] =Σ_(m≥2) [−ln(m−1)+ln(m)−(1/m)] =lim_(x→∞) .Σ_(m=2) ^x −ln(m−1)+ln(m)−(1/m)] =lim_(x→∞) ln(x)−Σ_(m=2) ^x (1/m) =−lim_(x→∞) {Σ_(m=2) ^x (1/m)−ln(x)} =−lim_(x→∞) {Σ_(m=1) ^x (1/m)−ln(x)−1}=−{γ−1}=1−γ γ Euler mechorini constent](Q82478.png) | ||
| ||