
Question and Answers Forum
Question Number 82520 by peter frank last updated on 22/Feb/20

Commented by mathmax by abdo last updated on 22/Feb/20
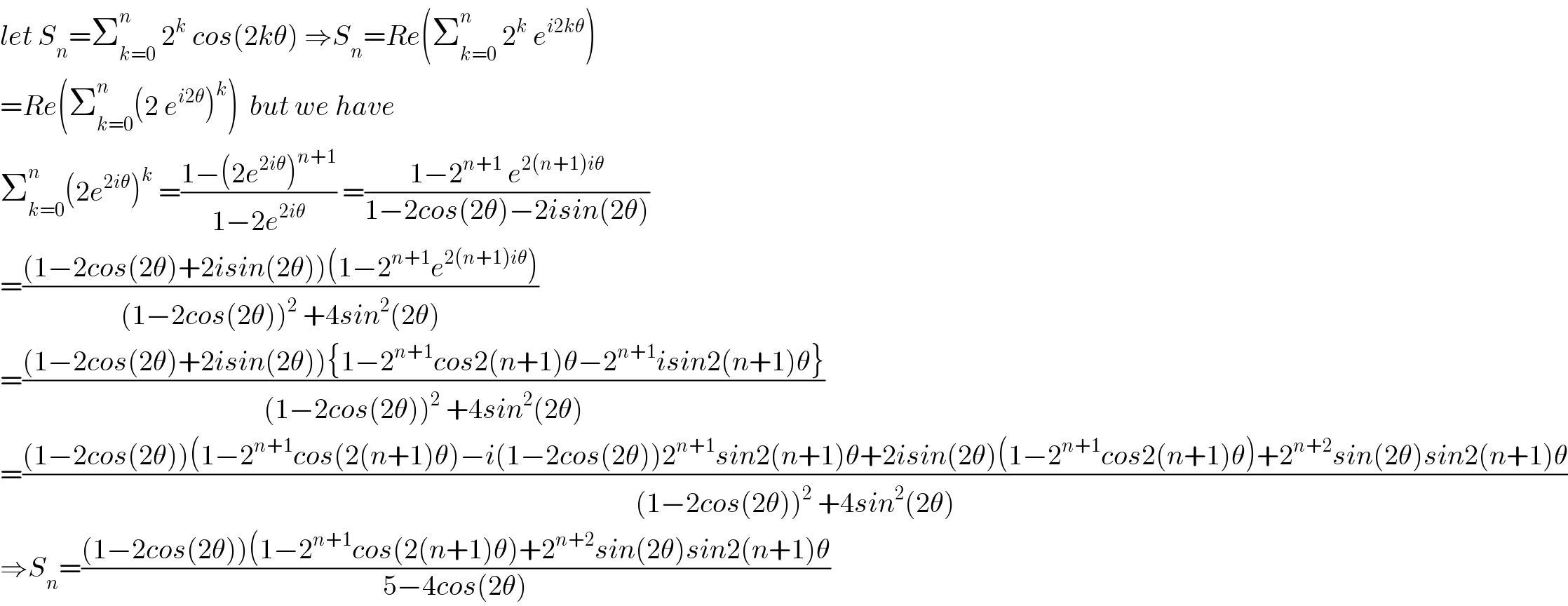
Answered by mr W last updated on 22/Feb/20
![z=2(cos θ+i sin θ)=2e^(iθ) z^k =2^k (cos kθ+i sin kθ)=(2e^(iθ) )^k z^0 +z^1 +z^2 +...+z^n =Σ_(k=0) ^n (2e^(iθ) )^k ← sum of GP Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=(((2e^(iθ) )^(n+1) −1)/(2e^(iθ) −1)) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=((2^(n+1) e^(i(n+1)θ) −1)/(2e^(iθ) −1)) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=((2^(n+1) [cos (n+1)θ+i sin (n+1)θ]−1)/(2(cos θ+i sin θ)−1)) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=(({[2^(n+1) cos (n+1)θ−1]+i [2^(n+1) sin (n+1)θ]}[(2cos θ−1)−i sin θ])/([(2cos θ−1)+i sin θ][(2cos θ−1)−i sin θ])) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=(({[2^(n+1) cos (n+1)θ−1](2cos θ−1)+2^(n+1) sin (n+1)θ sin θ}+i {[2^(n+1) sin (n+1)θ](2cos θ−1)−[2^(n+1) cos (n+1)θ−1]sin θ})/((2cos θ−1)^2 +sin^2 θ)) ⇒Σ_(k=0) ^n 2^k cos (kθ)=(([2^(n+1) cos (n+1)θ−1](2cos θ−1)+2^(n+1) sin θ sin (n+1)θ)/((2cos θ−1)^2 +sin^2 θ)) ⇒Σ_(k=0) ^n 2^k sin (kθ)=((2^(n+1) (2 cos θ−1) sin (n+1)θ−[2^(n+1) cos (n+1)θ−1]sin θ)/((2cos θ−1)^2 +sin^2 θ))](Q82534.png)
Commented by peter frank last updated on 22/Feb/20
| ||
Question and Answers Forum | ||
Question Number 82520 by peter frank last updated on 22/Feb/20 | ||
 | ||
Commented by mathmax by abdo last updated on 22/Feb/20 | ||
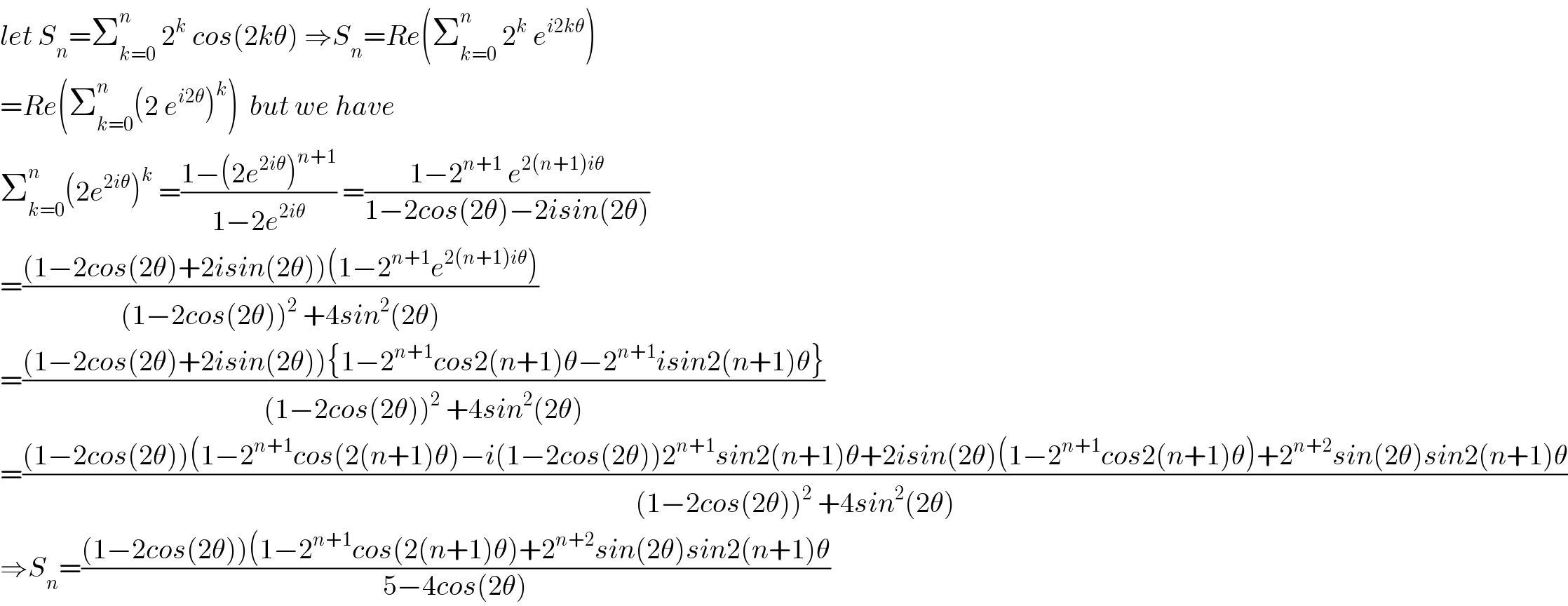 | ||
Answered by mr W last updated on 22/Feb/20 | ||
![z=2(cos θ+i sin θ)=2e^(iθ) z^k =2^k (cos kθ+i sin kθ)=(2e^(iθ) )^k z^0 +z^1 +z^2 +...+z^n =Σ_(k=0) ^n (2e^(iθ) )^k ← sum of GP Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=(((2e^(iθ) )^(n+1) −1)/(2e^(iθ) −1)) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=((2^(n+1) e^(i(n+1)θ) −1)/(2e^(iθ) −1)) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=((2^(n+1) [cos (n+1)θ+i sin (n+1)θ]−1)/(2(cos θ+i sin θ)−1)) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=(({[2^(n+1) cos (n+1)θ−1]+i [2^(n+1) sin (n+1)θ]}[(2cos θ−1)−i sin θ])/([(2cos θ−1)+i sin θ][(2cos θ−1)−i sin θ])) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=(({[2^(n+1) cos (n+1)θ−1](2cos θ−1)+2^(n+1) sin (n+1)θ sin θ}+i {[2^(n+1) sin (n+1)θ](2cos θ−1)−[2^(n+1) cos (n+1)θ−1]sin θ})/((2cos θ−1)^2 +sin^2 θ)) ⇒Σ_(k=0) ^n 2^k cos (kθ)=(([2^(n+1) cos (n+1)θ−1](2cos θ−1)+2^(n+1) sin θ sin (n+1)θ)/((2cos θ−1)^2 +sin^2 θ)) ⇒Σ_(k=0) ^n 2^k sin (kθ)=((2^(n+1) (2 cos θ−1) sin (n+1)θ−[2^(n+1) cos (n+1)θ−1]sin θ)/((2cos θ−1)^2 +sin^2 θ))](Q82534.png) | ||
| ||
Commented by peter frank last updated on 22/Feb/20 | ||
 | ||