Question Number 82573 by Power last updated on 22/Feb/20
Commented by Tony Lin last updated on 22/Feb/20
![let x=asecθ, dx=asecθtanθdθ ⇒secθ=(x/a), tanθ=((√(x^2 −a^2 ))/a) a^2 ∫tan^2 θsecθdθ =a^2 ∫(sec^2 θ−1)secθdθ =a^2 [∫sec^3 θdθ−∫secθdθ] ∫sec^3 dθ =secθtanθ−∫tan^2 θsecθdθ =secθtanθ−∫(sec^2 θ−1)secθdθ =secθtanθ−∫sec^3 dθ+∫secθdθ ⇒∫sec^3 dθ =(1/2)(secθtanθ+ln∣secθ+tanθ∣)+c ∴a^2 ∫tan^2 θsecθdθ =(1/2)a^2 (secθtanθ−ln∣secθ+tanθ∣)+c =(1/2)(x(√(x^2 −a^2 ))−aln∣x+(√(x^2 −a^2 ))∣)+c](Q82581.png)
$${let}\:{x}={asec}\theta,\:{dx}={asec}\theta{tan}\theta{d}\theta \\ $$$$\Rightarrow{sec}\theta=\frac{{x}}{{a}},\:{tan}\theta=\frac{\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}} \\ $$$${a}^{\mathrm{2}} \int{tan}^{\mathrm{2}} \theta{sec}\theta{d}\theta \\ $$$$={a}^{\mathrm{2}} \int\left({sec}^{\mathrm{2}} \theta−\mathrm{1}\right){sec}\theta{d}\theta \\ $$$$={a}^{\mathrm{2}} \left[\int{sec}^{\mathrm{3}} \theta{d}\theta−\int{sec}\theta{d}\theta\right] \\ $$$$\int{sec}^{\mathrm{3}} {d}\theta \\ $$$$={sec}\theta{tan}\theta−\int{tan}^{\mathrm{2}} \theta{sec}\theta{d}\theta \\ $$$$={sec}\theta{tan}\theta−\int\left({sec}^{\mathrm{2}} \theta−\mathrm{1}\right){sec}\theta{d}\theta \\ $$$$={sec}\theta{tan}\theta−\int{sec}^{\mathrm{3}} {d}\theta+\int{sec}\theta{d}\theta \\ $$$$\Rightarrow\int{sec}^{\mathrm{3}} {d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({sec}\theta{tan}\theta+{ln}\mid{sec}\theta+{tan}\theta\mid\right)+{c} \\ $$$$\therefore{a}^{\mathrm{2}} \int{tan}^{\mathrm{2}} \theta{sec}\theta{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{2}} \left({sec}\theta{tan}\theta−{ln}\mid{sec}\theta+{tan}\theta\mid\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }−{aln}\mid{x}+\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }\mid\right)+{c} \\ $$
Commented by mathmax by abdo last updated on 22/Feb/20
$${A}\:=\int\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx}\:{changement}\:{x}={ach}\left({t}\right)\:{give} \\ $$$${A}\:=\int\mid{a}\mid{sh}\left({t}\right){a}\:{sh}\left({t}\right){dt}\:={a}\mid{a}\mid\int\:{sh}^{\mathrm{2}} {t}\:{dt} \\ $$$$={a}\mid{a}\mid\:\int\:\:\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}\:=\frac{{a}\mid{a}\mid}{\mathrm{2}}\:\int\:{ch}\left(\mathrm{2}{t}\right){dt}−\frac{{a}\mid{a}\mid{t}}{\mathrm{2}} \\ $$$$=\frac{{a}\mid{a}\mid}{\mathrm{4}}{sh}\left(\mathrm{2}{t}\right)−\frac{{a}\mid{a}\mid}{\mathrm{2}}{t}\:+{c}\:=\frac{{a}\mid{a}\mid}{\mathrm{2}}{sh}\left({t}\right){ch}\left({t}\right)−\frac{{a}\mid{a}\mid}{\mathrm{2}}{t}\:+{c} \\ $$$$=\frac{{a}\mid{a}\mid}{\mathrm{2}}\sqrt{\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\mathrm{1}}×\frac{{x}}{{a}}\:−\frac{{a}\mid{a}\mid}{\mathrm{2}}\:{argch}\left(\frac{{x}}{{a}}\right)+{C} \\ $$$$=\frac{{a}\mid{a}\mid}{\mathrm{2}\mid{a}\mid{a}}{x}\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:−\frac{{a}\mid{a}\mid}{\mathrm{2}}{ln}\left(\frac{{x}}{{a}}+\sqrt{\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\mathrm{1}}\right)\:+{C} \\ $$$$=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} \:}−\frac{{a}\mid{a}\mid}{\mathrm{2}}{ln}\left(\frac{{x}}{{a}}+\frac{\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{\mid{a}\mid}\right)\:+{C} \\ $$
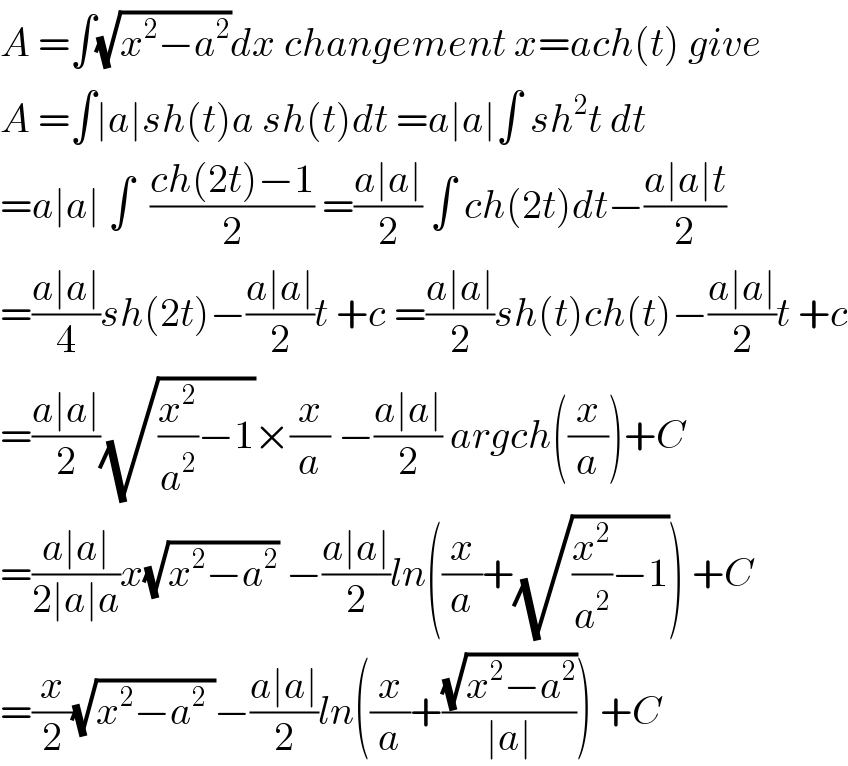
Commented by Power last updated on 22/Feb/20
$$\mathrm{thanks} \\ $$
Commented by msup trace by abdo last updated on 22/Feb/20
$${you}\:{are}\:{welcome} \\ $$