Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 8267 by lepan last updated on 04/Oct/16

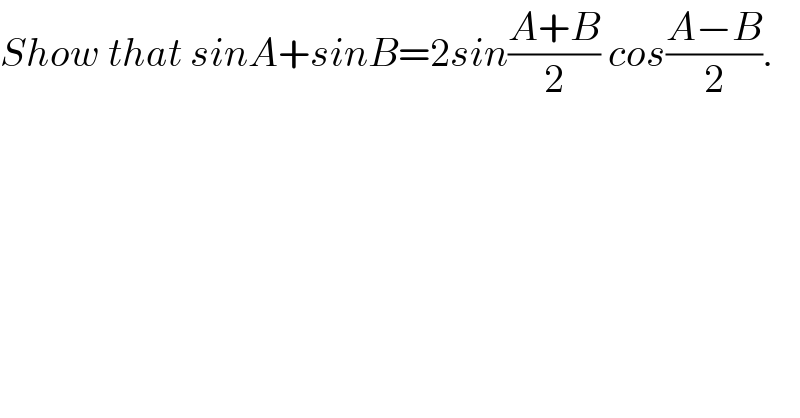
Show that sinA+sinB=2sin((A+B)/2) cos((A−B)/2).

$${Show}\:{that}\:{sinA}+{sinB}=\mathrm{2}{sin}\frac{{A}+{B}}{\mathrm{2}}\:{cos}\frac{{A}−{B}}{\mathrm{2}}. \\ $$$$ \\ $$

Answered by Yozzias last updated on 04/Oct/16

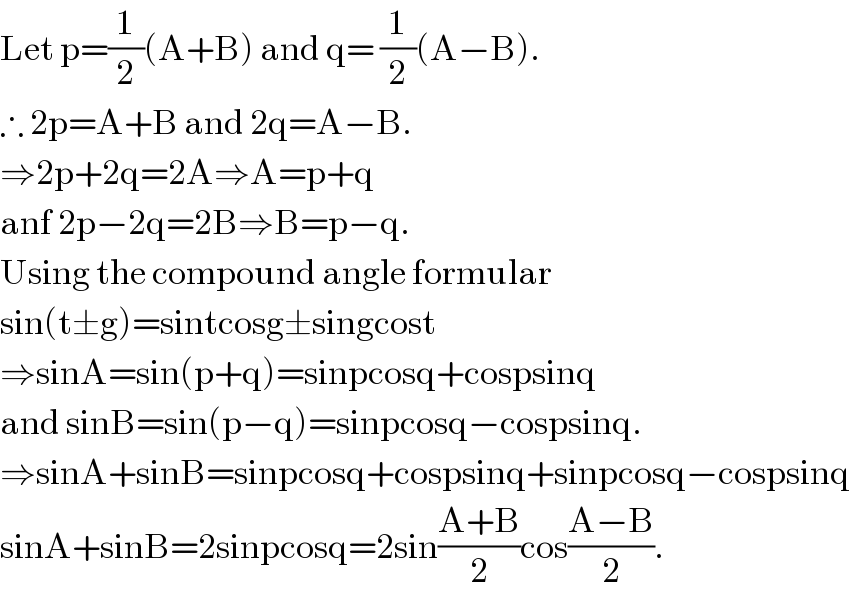
Let p=(1/2)(A+B) and q= (1/2)(A−B). ∴ 2p=A+B and 2q=A−B. ⇒2p+2q=2A⇒A=p+q anf 2p−2q=2B⇒B=p−q. Using the compound angle formular sin(t±g)=sintcosg±singcost ⇒sinA=sin(p+q)=sinpcosq+cospsinq and sinB=sin(p−q)=sinpcosq−cospsinq. ⇒sinA+sinB=sinpcosq+cospsinq+sinpcosq−cospsinq sinA+sinB=2sinpcosq=2sin((A+B)/2)cos((A−B)/2).

$$\mathrm{Let}\:\mathrm{p}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}+\mathrm{B}\right)\:\mathrm{and}\:\mathrm{q}=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}−\mathrm{B}\right). \\ $$$$\therefore\:\mathrm{2p}=\mathrm{A}+\mathrm{B}\:\mathrm{and}\:\mathrm{2q}=\mathrm{A}−\mathrm{B}. \\ $$$$\Rightarrow\mathrm{2p}+\mathrm{2q}=\mathrm{2A}\Rightarrow\mathrm{A}=\mathrm{p}+\mathrm{q}\: \\ $$$$\mathrm{anf}\:\mathrm{2p}−\mathrm{2q}=\mathrm{2B}\Rightarrow\mathrm{B}=\mathrm{p}−\mathrm{q}. \\ $$$$\mathrm{Using}\:\mathrm{the}\:\mathrm{compound}\:\mathrm{angle}\:\mathrm{formular} \\ $$$$\mathrm{sin}\left(\mathrm{t}\pm\mathrm{g}\right)=\mathrm{sintcosg}\pm\mathrm{singcost} \\ $$$$\Rightarrow\mathrm{sinA}=\mathrm{sin}\left(\mathrm{p}+\mathrm{q}\right)=\mathrm{sinpcosq}+\mathrm{cospsinq} \\ $$$$\mathrm{and}\:\mathrm{sinB}=\mathrm{sin}\left(\mathrm{p}−\mathrm{q}\right)=\mathrm{sinpcosq}−\mathrm{cospsinq}. \\ $$$$\Rightarrow\mathrm{sinA}+\mathrm{sinB}=\mathrm{sinpcosq}+\mathrm{cospsinq}+\mathrm{sinpcosq}−\mathrm{cospsinq} \\ $$$$\mathrm{sinA}+\mathrm{sinB}=\mathrm{2sinpcosq}=\mathrm{2sin}\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}\mathrm{cos}\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com