Question Number 82761 by TANMAY PANACEA last updated on 24/Feb/20
![lim_(x→0) (((cosx)^(1/m) −(cosx)^(1/n) )/x^2 ) [where m and n integer]](Q82761.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} −\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} }{{x}^{\mathrm{2}} }\:\:\left[{where}\:{m}\:{and}\:{n}\:{integer}\right] \\ $$
Commented by mr W last updated on 24/Feb/20
![lim_(x→0) (((cosx)^(1/m) −(cosx)^(1/n) )/x^2 ) =lim_(x→0) (((1−2 sin^2 (x/2))^(1/m) −(1−2 sin^2 (x/2))^(1/n) )/x^2 ) =lim_(x→0) ((1−(2/m) sin^2 (x/2)+o(sin^2 (x/2))−[1−(2/n) sin^2 (x/2)+o(sin^2 (x/2))])/x^2 ) =lim_(x→0) ((2((1/n)−(1/m)) sin^2 (x/2))/x^2 ) =(1/2)((1/n)−(1/m))lim_(x→0) ((( sin (x/2))/(x/2)))^2 =(1/2)((1/n)−(1/m))](Q82762.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} −\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} }{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{m}}} −\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{n}}} }{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{\mathrm{2}}{{m}}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}+{o}\left(\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)−\left[\mathrm{1}−\frac{\mathrm{2}}{{n}}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}+{o}\left(\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)\right]}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{m}}\right)\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}}{{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{m}}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\:\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}{\frac{{x}}{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{m}}\right) \\ $$
Commented by TANMAY PANACEA last updated on 24/Feb/20
$${excellent}\:{sir}... \\ $$
Commented by jagoll last updated on 24/Feb/20
$${sir}\:{what}\:{is}\:{o}\left(\mathrm{sin}\:^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right) \\ $$
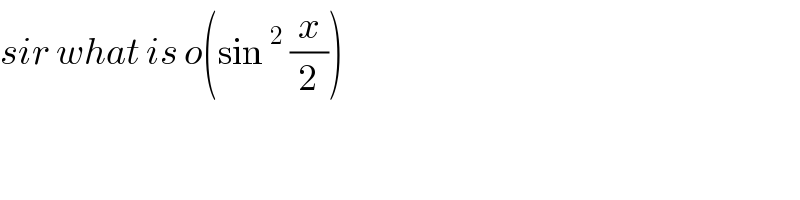
Commented by abdomathmax last updated on 24/Feb/20
$${let}\:{f}\left({x}\right)=\frac{\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} −\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} }{{x}^{\mathrm{2}} }\:\:{we}\:{hsve}\:{for}\:{x}\rightarrow\mathrm{0} \\ $$$${cosx}\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} \:\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}{m}}\:{and} \\ $$$$\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} \sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}{n}}\:\Rightarrow\left({cosx}\right)^{\frac{\mathrm{1}}{{m}}} −\left({cosx}\right)^{\frac{\mathrm{1}}{{n}}} \:\sim{x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{m}}\right) \\ $$$$\Rightarrow{f}\left({x}\right)\sim\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{m}−{n}}{{mn}}\right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{f}\left({x}\right)=\frac{{m}−{n}}{\mathrm{2}{mn}} \\ $$
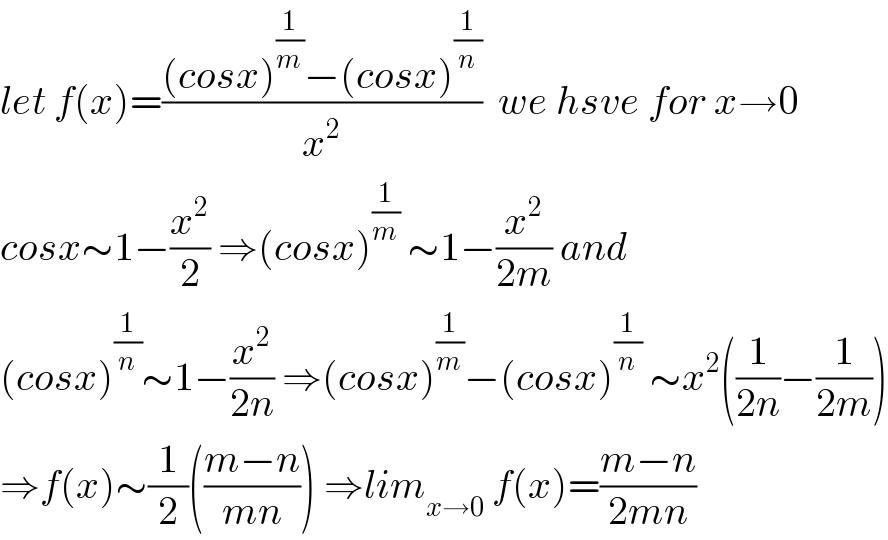
Commented by mr W last updated on 24/Feb/20
$${to}\:{jagoll}\:{sir}: \\ $$$${o}\left({x}^{\mathrm{2}} \right)\:{stands}\:{for}\:{terms}\:{with}\:{higher}\:{orders} \\ $$$${than}\:{x}^{\mathrm{2}} .\:{for}\:{example}: \\ $$$$\mathrm{cos}\:{x}=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{6}!}+...... \\ $$$$=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+{o}\left({x}^{\mathrm{4}} \right) \\ $$$$=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$ \\ $$$${search}\:{in}\:{google}\:{for}\:``{little}\:{o}\:{notation}'' \\ $$$${for}\:{more}. \\ $$
Commented by jagoll last updated on 24/Feb/20
$${thank}\:{you}\:.\:{sir}\: \\ $$
Commented by mathmax by abdo last updated on 24/Feb/20
$${the}\:{small}\:{o}\left({x}^{\mathrm{2}} \right)={x}^{\mathrm{2}} \delta\left({x}\right)\:\:{with}\:{lim}_{{x}\rightarrow\mathrm{0}} \delta\left({x}\right)=\mathrm{0} \\ $$