
Question Number 8282 by tawakalitu last updated on 06/Oct/16
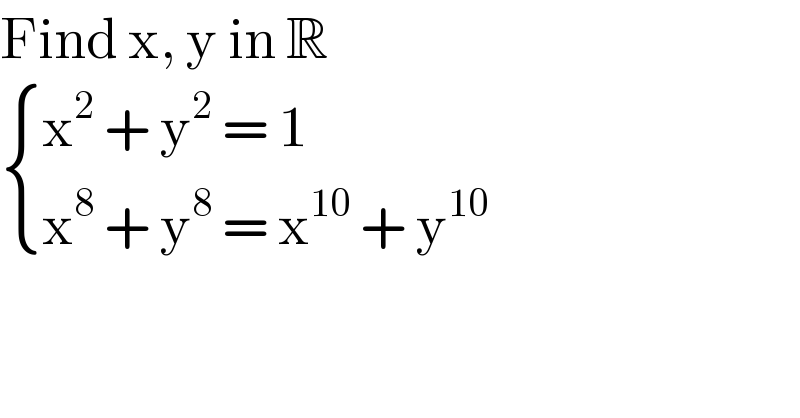
$$\mathrm{Find}\:\mathrm{x},\:\mathrm{y}\:\mathrm{in}\:\mathbb{R} \\ $$$$\begin{cases}{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{1}}\\{\mathrm{x}^{\mathrm{8}} \:+\:\mathrm{y}^{\mathrm{8}} \:=\:\mathrm{x}^{\mathrm{10}} \:+\:\mathrm{y}^{\mathrm{10}} }\end{cases} \\ $$
Commented by Rasheed Soomro last updated on 06/Oct/16

$$\mathcal{V}\:\:\mathcal{N}{ice}! \\ $$
Commented by sou1618 last updated on 06/Oct/16
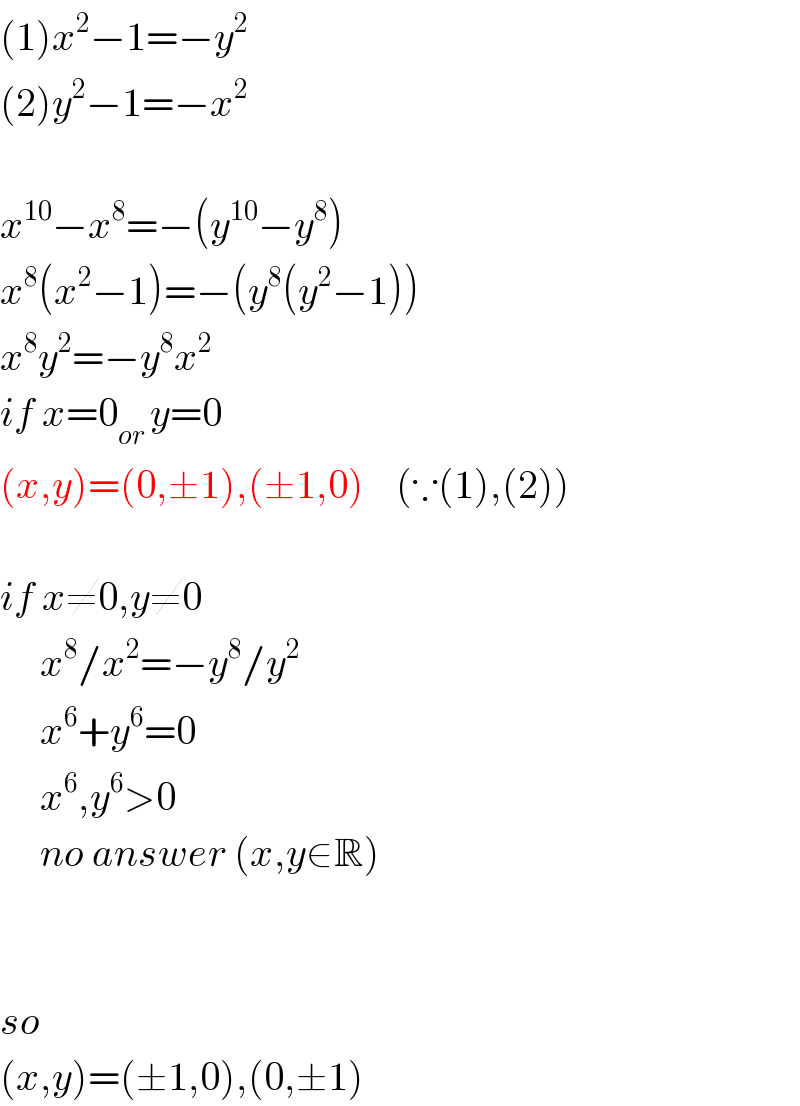
$$\left(\mathrm{1}\right){x}^{\mathrm{2}} −\mathrm{1}=−{y}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right){y}^{\mathrm{2}} −\mathrm{1}=−{x}^{\mathrm{2}} \\ $$$$ \\ $$$${x}^{\mathrm{10}} −{x}^{\mathrm{8}} =−\left({y}^{\mathrm{10}} −{y}^{\mathrm{8}} \right) \\ $$$${x}^{\mathrm{8}} \left({x}^{\mathrm{2}} −\mathrm{1}\right)=−\left({y}^{\mathrm{8}} \left({y}^{\mathrm{2}} −\mathrm{1}\right)\right) \\ $$$${x}^{\mathrm{8}} {y}^{\mathrm{2}} =−{y}^{\mathrm{8}} {x}^{\mathrm{2}} \\ $$$${if}\:{x}=\mathrm{0}_{{or}\:} {y}=\mathrm{0} \\ $$$$\left({x},{y}\right)=\left(\mathrm{0},\pm\mathrm{1}\right),\left(\pm\mathrm{1},\mathrm{0}\right)\:\:\:\:\left(\because\left(\mathrm{1}\right),\left(\mathrm{2}\right)\right) \\ $$$$ \\ $$$${if}\:{x}\neq\mathrm{0},{y}\neq\mathrm{0} \\ $$$$\:\:\:\:\:{x}^{\mathrm{8}} /{x}^{\mathrm{2}} =−{y}^{\mathrm{8}} /{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:{x}^{\mathrm{6}} +{y}^{\mathrm{6}} =\mathrm{0} \\ $$$$\:\:\:\:\:{x}^{\mathrm{6}} ,{y}^{\mathrm{6}} >\mathrm{0} \\ $$$$\:\:\:\:\:{no}\:{answer}\:\left({x},{y}\in\mathbb{R}\right) \\ $$$$ \\ $$$$ \\ $$$${so} \\ $$$$\left({x},{y}\right)=\left(\pm\mathrm{1},\mathrm{0}\right),\left(\mathrm{0},\pm\mathrm{1}\right) \\ $$
Commented by tawakalitu last updated on 06/Oct/16
$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much} \\ $$
Answered by nume1114 last updated on 06/Oct/16
![{ ((x^2 +y^2 =1...(i))),((x^8 +y^8 =x^(10) +y^(10) ...(ii))) :} From(i) (x^8 +y^8 )(x^2 +y^2 )=(x^8 +y^8 )×1=x^8 +y^8 x^8 +y^8 =(x^8 +y^8 )(x^2 +y^2 ) =x^(10) +y^(10) +x^2 y^8 +x^8 y^2 ...(iii) From(ii),(iii) x^(10) +y^(10) +x^2 y^8 +x^8 y^2 =x^(10) +y^(10) x^2 y^8 +x^8 y^2 =0 x^2 y^8 +x^8 y^2 =x^2 y^2 (x^6 +y^6 ) =x^2 y^2 [(x^2 +y^2 )^3 −3x^2 y^2 (x^2 +y^2 )] =x^2 y^2 (1−3x^2 y^2 )=0(from (i)) y^2 =0 or (1/3) if x^2 y^2 =0 x=0 or y=0 when { ((x=0)),((y=0)) :},from(i), { ((y=±1)),((x=±1)) :} if x^2 y^2 =(1/3) (t−x^2 )(t−y^2 )=0⇔t=x^2 ,y^2 (t−x^2 )(t−y^2 )=t^2 −(x^2 +y^2 )t+x^2 y^2 =t^2 −t+(1/3) t^2 −t+(1/3)=0 D=1−(4/3)<0 so,(x,y)=(±1,0),(0,±1)](Q8284.png)
$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}...\left({i}\right)}\\{{x}^{\mathrm{8}} +{y}^{\mathrm{8}} ={x}^{\mathrm{10}} +{y}^{\mathrm{10}} ...\left({ii}\right)}\end{cases} \\ $$$${From}\left({i}\right) \\ $$$$\left({x}^{\mathrm{8}} +{y}^{\mathrm{8}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\left({x}^{\mathrm{8}} +{y}^{\mathrm{8}} \right)×\mathrm{1}={x}^{\mathrm{8}} +{y}^{\mathrm{8}} \\ $$$${x}^{\mathrm{8}} +{y}^{\mathrm{8}} =\left({x}^{\mathrm{8}} +{y}^{\mathrm{8}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{10}} +{y}^{\mathrm{10}} +{x}^{\mathrm{2}} {y}^{\mathrm{8}} +{x}^{\mathrm{8}} {y}^{\mathrm{2}} ...\left({iii}\right) \\ $$$${From}\left({ii}\right),\left({iii}\right) \\ $$$${x}^{\mathrm{10}} +{y}^{\mathrm{10}} +{x}^{\mathrm{2}} {y}^{\mathrm{8}} +{x}^{\mathrm{8}} {y}^{\mathrm{2}} ={x}^{\mathrm{10}} +{y}^{\mathrm{10}} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{8}} +{x}^{\mathrm{8}} {y}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{8}} +{x}^{\mathrm{8}} {y}^{\mathrm{2}} ={x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{6}} +{y}^{\mathrm{6}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} {y}^{\mathrm{2}} \left[\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} {y}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)=\mathrm{0}\left({from}\:\left({i}\right)\right) \\ $$$${y}^{\mathrm{2}} =\mathrm{0}\:{or}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${if}\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\mathrm{0}\:{or}\:{y}=\mathrm{0} \\ $$$$\:{when}\:\begin{cases}{{x}=\mathrm{0}}\\{{y}=\mathrm{0}}\end{cases},{from}\left({i}\right),\begin{cases}{{y}=\pm\mathrm{1}}\\{{x}=\pm\mathrm{1}}\end{cases} \\ $$$${if}\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left({t}−{x}^{\mathrm{2}} \right)\left({t}−{y}^{\mathrm{2}} \right)=\mathrm{0}\Leftrightarrow{t}={x}^{\mathrm{2}} ,{y}^{\mathrm{2}} \\ $$$$\left({t}−{x}^{\mathrm{2}} \right)\left({t}−{y}^{\mathrm{2}} \right)={t}^{\mathrm{2}} −\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){t}+{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={t}^{\mathrm{2}} −{t}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${t}^{\mathrm{2}} −{t}+\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{0} \\ $$$${D}=\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}<\mathrm{0} \\ $$$${so},\left({x},{y}\right)=\left(\pm\mathrm{1},\mathrm{0}\right),\left(\mathrm{0},\pm\mathrm{1}\right)\: \\ $$
Commented by Rasheed Soomro last updated on 06/Oct/16

$$\mathcal{N}{ice}! \\ $$
Commented by tawakalitu last updated on 06/Oct/16
$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much} \\ $$
