Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 82867 by mind is power last updated on 24/Feb/20

$$helloprovethat{\int }_0^{+\mathrm{\infty }}sin\left(x^4\right)dx=sin\left(\frac{\pi }{8}\right){\int }_0^{+\mathrm{\infty }}{e}^{-x^4}dx?$$$$verrynicedayGoodBlessYou$$

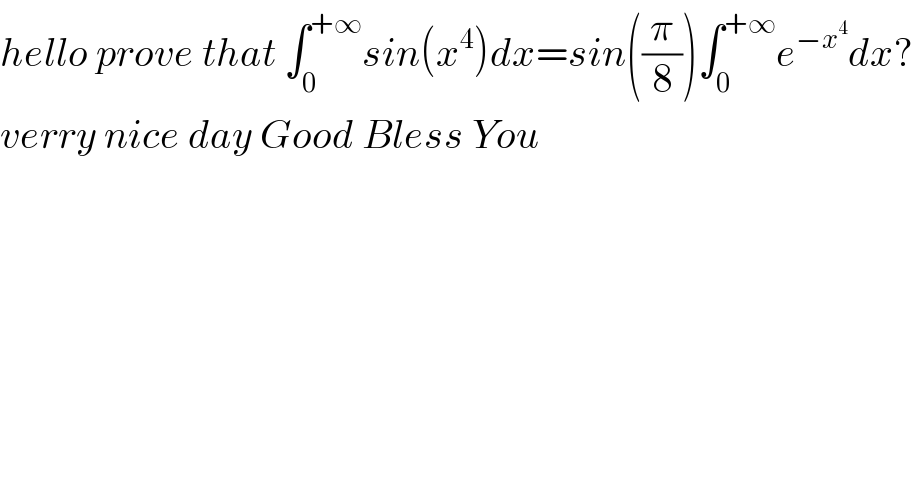
Commented by abdomathmax last updated on 25/Feb/20

$${\int }_0^{\mathrm{\infty }}sin\left(x^4\right)dx=Im\left({\int }_0^{\mathrm{\infty }}{e}^{{ix}^4}dx\right)butchsngement$$$${ix}^4=-t^{4}give{x}^4={it}^4\Rightarrow x=i^{\frac{1}{4}}t\Rightarrow$$$${\int }_0^{\mathrm{\infty }}{e}^{{ix}^4}dx={\int }_0^{\mathrm{\infty }}{e}^{-t^4}{i}^{\frac{1}{4}}dt={\left(e^{\frac{i\pi }{2}}\right)}^{\frac{1}{4}}{\int }_0^{\mathrm{\infty }}{e}^{-t^4}dt$$$$=e^{\frac{i\pi }{8}}{\int }_0^{\mathrm{\infty }}{e}^{-t^4}dt=(cos\left(\frac{\pi }{8}\right)+isin\left(\frac{\pi }{8}\right)){\int }_0^{\mathrm{\infty }}{e}^{-t^4}dt\Rightarrow$$$${\int }_0^{\mathrm{\infty }}sin\left(x^4\right)dx=sin\left(\frac{\pi }{8}\right){\int }_0^{\mathrm{\infty }}{e}^{-t^4}dt$$$$alsochang.t^4=ugivet=u^{\frac{1}{4}}\Rightarrow$$$${\int }_0^{\mathrm{\infty }}{e}^{-t^4}dt={\int }_0^{\mathrm{\infty }}{e}^{-u}\frac{1}{4}{u}^{\frac{1}{4}-1}du$$$$=\frac{1}{4}\mathrm{\Gamma }\left(\frac{1}{4}\right)\Rightarrow {\int }_0^{\mathrm{\infty }}sin\left(x^4\right)dx=\frac{1}{4}sin\left(\frac{\pi }{8}\right)\mathrm{\Gamma }\left(\frac{1}{4}\right)$$$$=\frac{\sqrt{2-\sqrt{2}}}{8}\times \mathrm{\Gamma }\left(\frac{1}{4}\right)$$

Commented by mind is power last updated on 25/Feb/20

$$nicesolutionSirthankyou$$

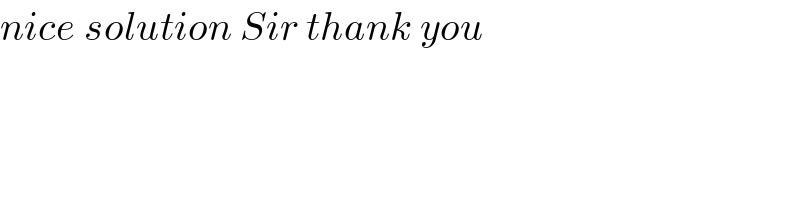
Commented by msup trace by abdo last updated on 25/Feb/20

$$youarewelcome$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com