
Question and Answers Forum
Question Number 82872 by abdomathmax last updated on 25/Feb/20
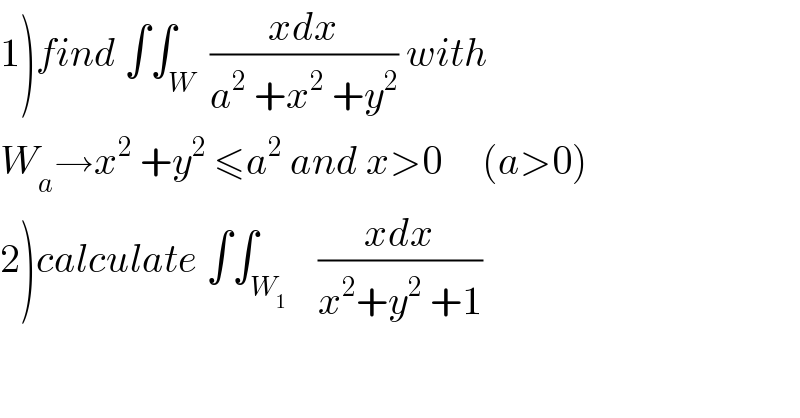
Commented bymathmax by abdo last updated on 25/Feb/20
![1) we use the diffeomorphism (r,θ)→(x,y)/x=rcosθ and y=rsinθ wehave x^2 +y^2 ≤a^2 ⇒0≤r≤a x>0 ⇒θ∈]−(π/2),(π/2)[ ⇒∫∫_W_a ((xdxdy)/(a^2 +r^2 )) =∫_0 ^a ∫_(−(π/2)) ^(π/2) ((rcosθ rdr dθ)/(a^2 +r^2 )) ∫_0 ^a (r^2 /(r^2 +a^2 )) dr ×∫_(−(π/2)) ^(π/2) cosθ dθ =2 ∫_0 ^a (r^2 /(r^2 +a^2 ))dr =2 ∫_0 ^a ((r^2 +a^2 −a^2 )/(r^2 +a^2 ))dr =2a −2a^2 ∫_0 ^a (dr/(r^2 +a^2 )) (ch. r=ax) =2a−2a^2 ∫_0 ^1 ((adx)/(a^2 (1+x^2 ))) =2a−2a [arctanx]_0 ^1 =2a−2a×(π/4) =(2−(π/2))a 2) ∫∫_W_1 ((xdx)/(x^2 +y^2 +1)) =_(a=1) 2−(π/2)](Q82916.png)
| ||
Question and Answers Forum | ||
Question Number 82872 by abdomathmax last updated on 25/Feb/20 | ||
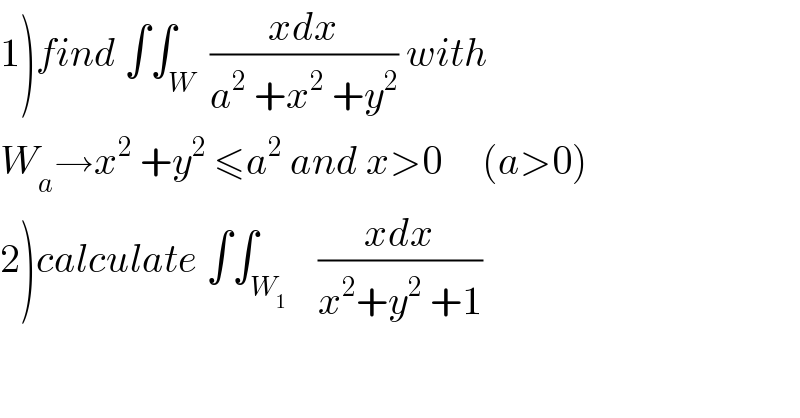 | ||
Commented bymathmax by abdo last updated on 25/Feb/20 | ||
![1) we use the diffeomorphism (r,θ)→(x,y)/x=rcosθ and y=rsinθ wehave x^2 +y^2 ≤a^2 ⇒0≤r≤a x>0 ⇒θ∈]−(π/2),(π/2)[ ⇒∫∫_W_a ((xdxdy)/(a^2 +r^2 )) =∫_0 ^a ∫_(−(π/2)) ^(π/2) ((rcosθ rdr dθ)/(a^2 +r^2 )) ∫_0 ^a (r^2 /(r^2 +a^2 )) dr ×∫_(−(π/2)) ^(π/2) cosθ dθ =2 ∫_0 ^a (r^2 /(r^2 +a^2 ))dr =2 ∫_0 ^a ((r^2 +a^2 −a^2 )/(r^2 +a^2 ))dr =2a −2a^2 ∫_0 ^a (dr/(r^2 +a^2 )) (ch. r=ax) =2a−2a^2 ∫_0 ^1 ((adx)/(a^2 (1+x^2 ))) =2a−2a [arctanx]_0 ^1 =2a−2a×(π/4) =(2−(π/2))a 2) ∫∫_W_1 ((xdx)/(x^2 +y^2 +1)) =_(a=1) 2−(π/2)](Q82916.png) | ||