
Question and Answers Forum
Question Number 82877 by M±th+et£s last updated on 25/Feb/20
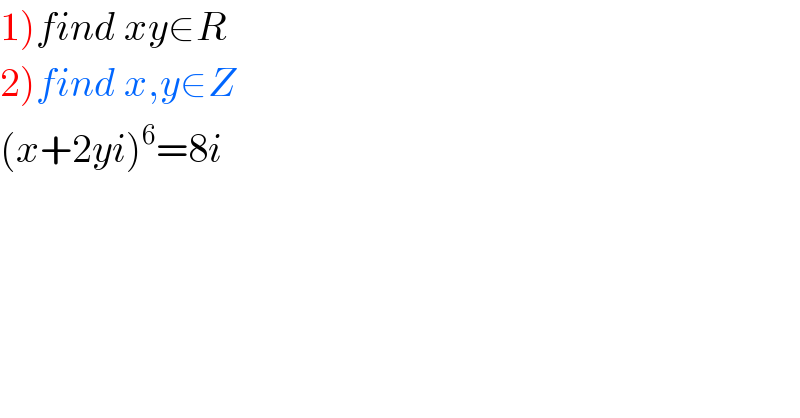
Commented by mr W last updated on 25/Feb/20
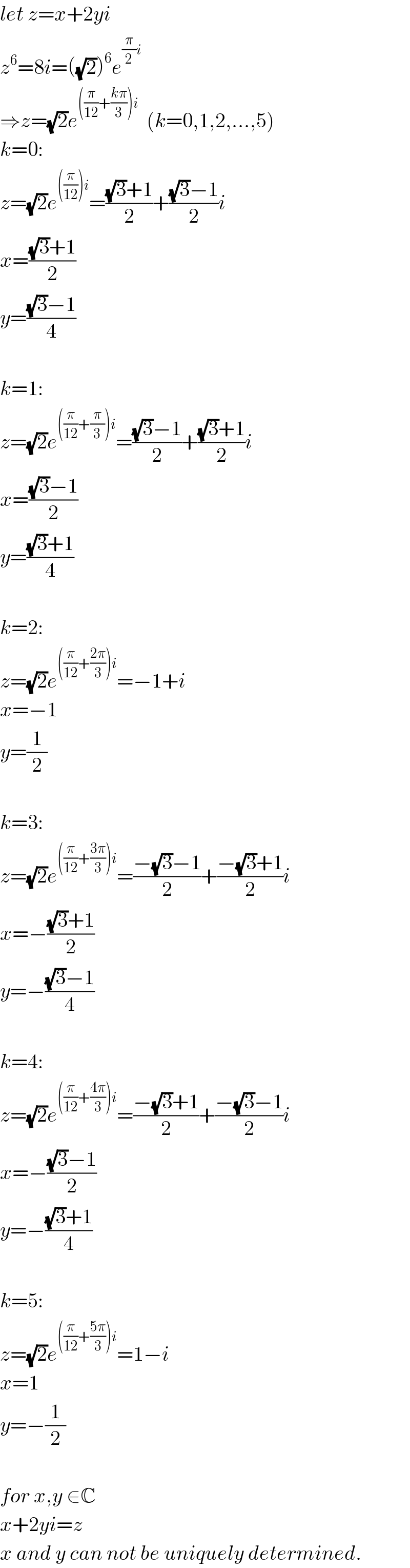
Answered by mind is power last updated on 25/Feb/20
![⇒(x−2yi)^6 =−8i ⇒(x^2 +4y^2 )^6 =64 ⇒x^2 +4y^2 =2 ⇒x=(√2)cos(θ) y=(1/(√2))sin(θ) θ∈[0,2π] ⇒8(e^(i6θ) )=8i ⇒6θ=(π/2)+2kπ⇒θ∈(π/(12))+((kπ)/3),k∈{0,......5} x=(√2)cos(θ),y=((sin(θ))/(√2)),θ∈{(π/(12))+((kπ)/3),0≤k≤5}](Q82895.png)
| ||
Question and Answers Forum | ||
Question Number 82877 by M±th+et£s last updated on 25/Feb/20 | ||
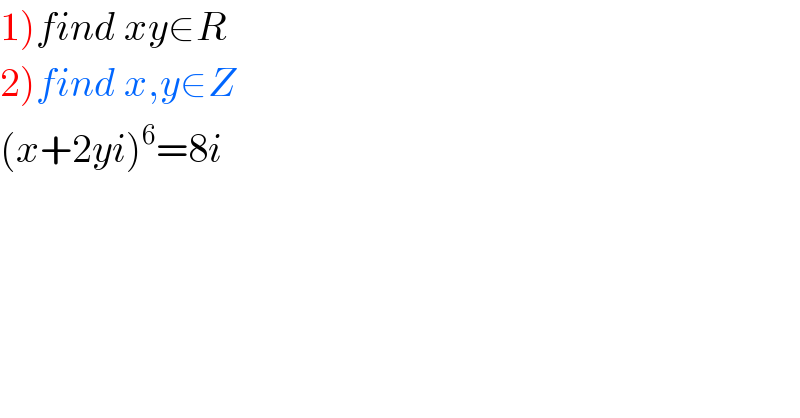 | ||
Commented by mr W last updated on 25/Feb/20 | ||
 | ||
Answered by mind is power last updated on 25/Feb/20 | ||
![⇒(x−2yi)^6 =−8i ⇒(x^2 +4y^2 )^6 =64 ⇒x^2 +4y^2 =2 ⇒x=(√2)cos(θ) y=(1/(√2))sin(θ) θ∈[0,2π] ⇒8(e^(i6θ) )=8i ⇒6θ=(π/2)+2kπ⇒θ∈(π/(12))+((kπ)/3),k∈{0,......5} x=(√2)cos(θ),y=((sin(θ))/(√2)),θ∈{(π/(12))+((kπ)/3),0≤k≤5}](Q82895.png) | ||
| ||