Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 82929 by VBash last updated on 26/Feb/20

$$if2B+A=45°$$$$showthat;$$$$tanB=\frac{1-2tanA-{tan}^{2}A}{1+2tanA-{tan}^{2}A}$$

Answered by jagoll last updated on 26/Feb/20

$$\mathrm{A}+\mathrm{B}={45}^{\mathrm{o}}-\mathrm{B}$$$$\tan (\mathrm{A}+\mathrm{B})=\tan ({45}^{\mathrm{o}}-\mathrm{B})$$$$\frac{\tan \mathrm{A}+\tan \mathrm{B}}{1-\tan \mathrm{A}.\tan \mathrm{B}}=\frac{1-\tan \mathrm{B}}{1+\tan \mathrm{B}}$$$$(\tan \mathrm{A}+\tan \mathrm{B})(1+\tan \mathrm{B})=$$$$(1-\mathrm{tanA}\tan \mathrm{B})(1-\tan \mathrm{B})$$$$\tan \mathrm{A}=\frac{\tan {}^2\mathrm{B}+2\tan \mathrm{B}-1}{\tan {}^2\mathrm{B}-2\tan \mathrm{B}-1}$$$$\mathrm{or}\tan \mathrm{A}=\frac{1-2\tan \mathrm{B}-\tan {}^2\mathrm{B}}{1+2\tan \mathrm{B}-\tan {}^2\mathrm{B}}$$$$$$

Commented by john santu last updated on 26/Feb/20

$$\mathrm{good}\mathrm{sir}$$

Commented by som(math1967) last updated on 26/Feb/20

$$Howtan(45°-B)=\frac{1-tanA}{1+tanA}???$$

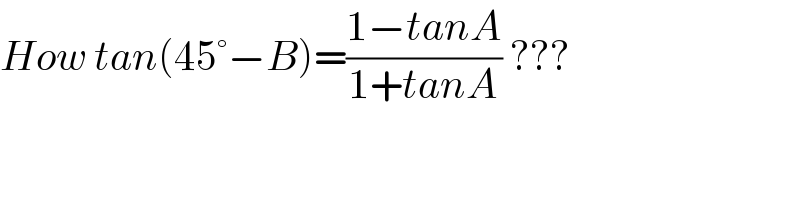
Commented by jagoll last updated on 26/Feb/20

$$\mathrm{hahaha}..\mathrm{sorry}.\mathrm{it}\mathrm{my}\mathrm{typo}$$

Answered by TANMAY PANACEA last updated on 26/Feb/20

$$tan\left(2B\right)=tan(45-A)$$$$lettanA=atanB=b$$$$\frac{2b}{1-b^2}=\frac{1-a}{1+a}$$$$\frac{2b+1-b^2}{2b-1+b^2}=\frac{1-a+1+a}{1-a-1-a}$$$$\frac{2b+1-b^2}{2b-1+b^2}=\frac{2}{-2a}$$$$\frac{-a}{1}=\frac{2b-1+b^2}{2b+1-b^2}$$$$a=\frac{b^2+2b-1}{b^2-2b-1}plsrecheckthequestion$$$$$$$$$$$$$$$$$$$$$$$$$$

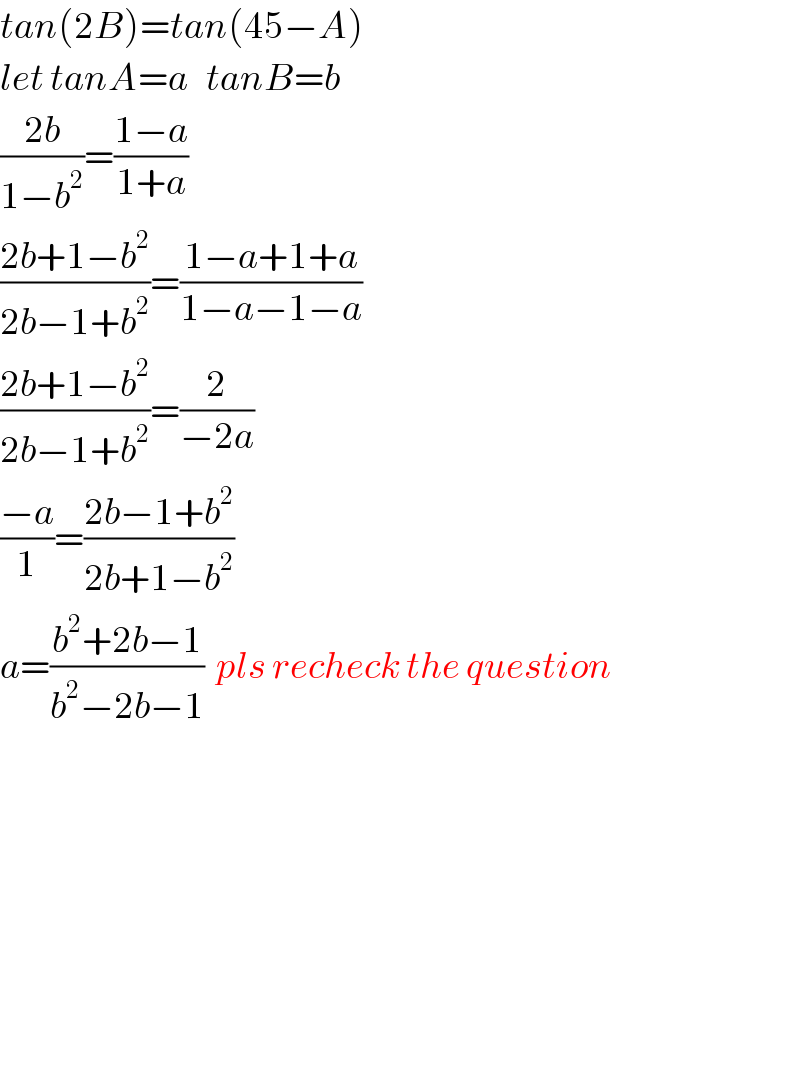
Commented by jagoll last updated on 26/Feb/20

$$\mathrm{it}\mathrm{that}\mathrm{the}\mathrm{question}\mathrm{wrong}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com