Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 82954 by john santu last updated on 26/Feb/20

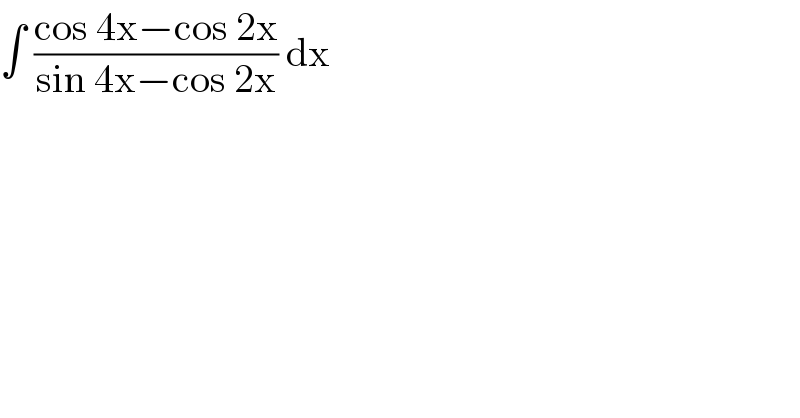
∫ ((cos 4x−cos 2x)/(sin 4x−cos 2x)) dx

$$\int\:\frac{\mathrm{cos}\:\mathrm{4x}−\mathrm{cos}\:\mathrm{2x}}{\mathrm{sin}\:\mathrm{4x}−\mathrm{cos}\:\mathrm{2x}}\:\mathrm{dx}\: \\ $$

Commented by john santu last updated on 26/Feb/20

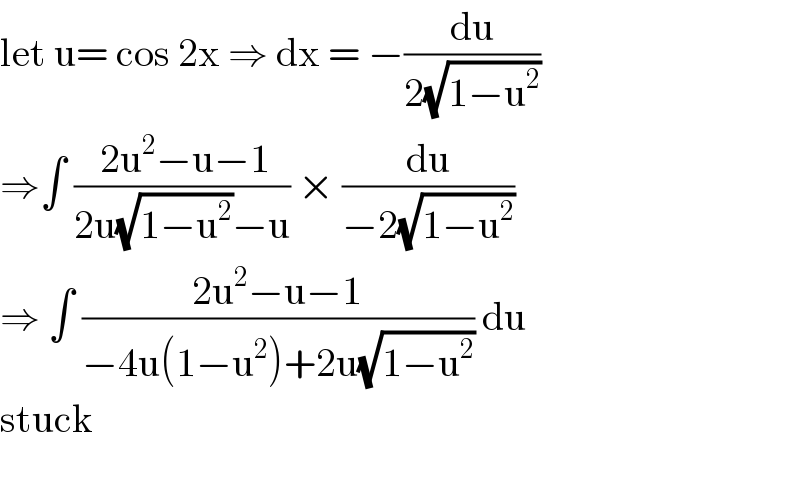
let u= cos 2x ⇒ dx = −(du/(2(√(1−u^2 )))) ⇒∫ (( 2u^2 −u−1)/(2u(√(1−u^2 ))−u)) × (du/(−2(√(1−u^2 )))) ⇒ ∫ ((2u^2 −u−1)/(−4u(1−u^2 )+2u(√(1−u^2 )))) du stuck

$$\mathrm{let}\:\mathrm{u}=\:\mathrm{cos}\:\mathrm{2x}\:\Rightarrow\:\mathrm{dx}\:=\:−\frac{\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }} \\ $$$$\Rightarrow\int\:\frac{\:\mathrm{2u}^{\mathrm{2}} −\mathrm{u}−\mathrm{1}}{\mathrm{2u}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }−\mathrm{u}}\:×\:\frac{\mathrm{du}}{−\mathrm{2}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\int\:\frac{\mathrm{2u}^{\mathrm{2}} −\mathrm{u}−\mathrm{1}}{−\mathrm{4u}\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)+\mathrm{2u}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}\:\mathrm{du} \\ $$$$\mathrm{stuck} \\ $$$$ \\ $$

Commented by MJS last updated on 26/Feb/20

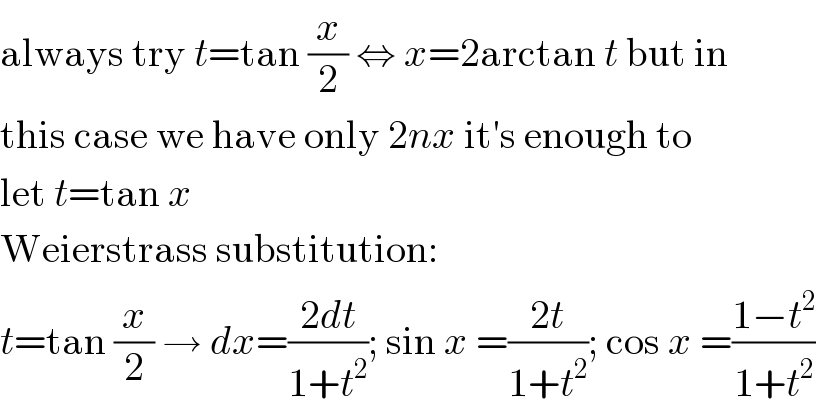
always try t=tan (x/2) ⇔ x=2arctan t but in this case we have only 2nx it′s enough to let t=tan x Weierstrass substitution: t=tan (x/2) → dx=((2dt)/(1+t^2 )); sin x =((2t)/(1+t^2 )); cos x =((1−t^2 )/(1+t^2 ))

$$\mathrm{always}\:\mathrm{try}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\Leftrightarrow\:{x}=\mathrm{2arctan}\:{t}\:\mathrm{but}\:\mathrm{in} \\ $$$$\mathrm{this}\:\mathrm{case}\:\mathrm{we}\:\mathrm{have}\:\mathrm{only}\:\mathrm{2}{nx}\:\mathrm{it}'\mathrm{s}\:\mathrm{enough}\:\mathrm{to} \\ $$$$\mathrm{let}\:{t}=\mathrm{tan}\:{x} \\ $$$$\mathrm{Weierstrass}\:\mathrm{substitution}: \\ $$$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} };\:\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} };\:\mathrm{cos}\:{x}\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$

Commented by john santu last updated on 26/Feb/20

o yes sir. i′m forgot this method. thank you mister mjs

$$\mathrm{o}\:\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}'\mathrm{m}\:\mathrm{forgot}\:\mathrm{this}\:\mathrm{method}. \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{mister}\:\mathrm{mjs} \\ $$

Answered by MJS last updated on 26/Feb/20

∫((cos 4x −cos 2x)/(sin 4x −cos 2x))dx= [t=tan x → dx=(dt/(t^2 +1))] =2∫(((t^2 −3)t^2 )/((t−1)(t+1)(t−2−(√3))(t−2+(√3))(t^2 +1)))dt= =(1/2)∫(dt/(t−1))+(1/6)∫(dt/(t+1))+((1+(√3))/6)∫(dt/(t−2−(√3)))+((1−(√3))/6)∫(dt/(t−2+(√3)))−∫(t/(t^2 +1))dt and all of them are easy to solve

$$\int\frac{\mathrm{cos}\:\mathrm{4}{x}\:−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{sin}\:\mathrm{4}{x}\:−\mathrm{cos}\:\mathrm{2}{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\mathrm{2}\int\frac{\left({t}^{\mathrm{2}} −\mathrm{3}\right){t}^{\mathrm{2}} }{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}−\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{2}+\sqrt{\mathrm{3}}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{dt}}{{t}+\mathrm{1}}+\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{dt}}{{t}−\mathrm{2}−\sqrt{\mathrm{3}}}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{6}}\int\frac{{dt}}{{t}−\mathrm{2}+\sqrt{\mathrm{3}}}−\int\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$\mathrm{and}\:\mathrm{all}\:\mathrm{of}\:\mathrm{them}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com