
Question and Answers Forum
Question Number 82970 by mathmax by abdo last updated on 26/Feb/20
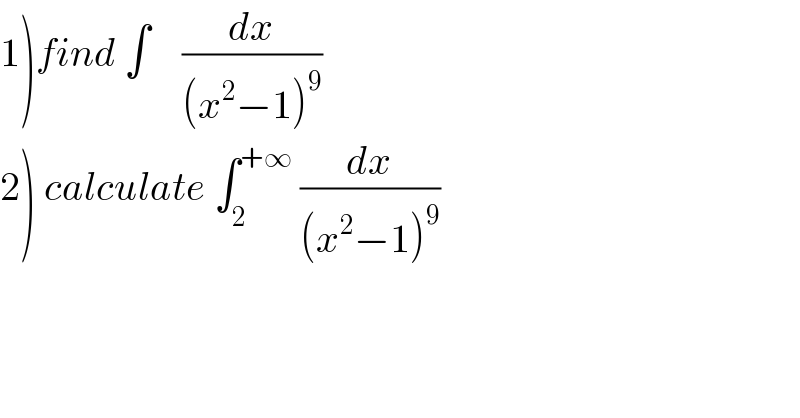
Commented by mathmax by abdo last updated on 26/Feb/20
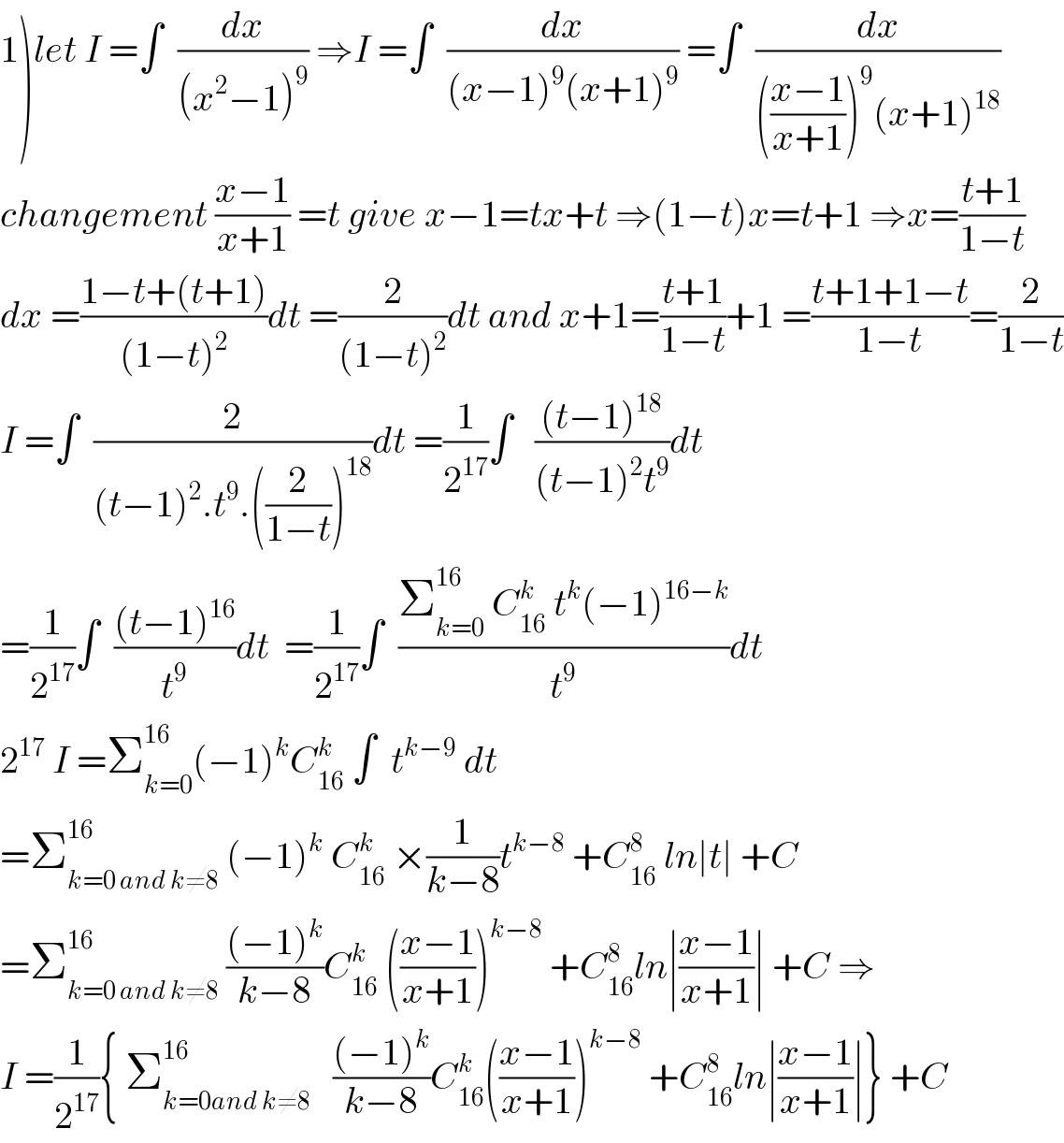
Commented by mathmax by abdo last updated on 26/Feb/20
![2) ∫_2 ^(+∞) (dx/((x^2 −1)^9 ))=(1/2^(17) )[Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k (((x−1)/(x+1)))^(k−8) +C_(16) ^8 ln∣((x−1)/(x+1))∣]_2 ^(+∞) =(1/2^(17) ){Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k −Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k ((1/3))^(k−8) −C_(16) ^8 ln((1/3))} =(1/2^(17) )Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k (1−(1/3^(k−8) ))+(C_(16) ^8 /2^(17) )ln(3)](Q83006.png)
| ||
Question and Answers Forum | ||
Question Number 82970 by mathmax by abdo last updated on 26/Feb/20 | ||
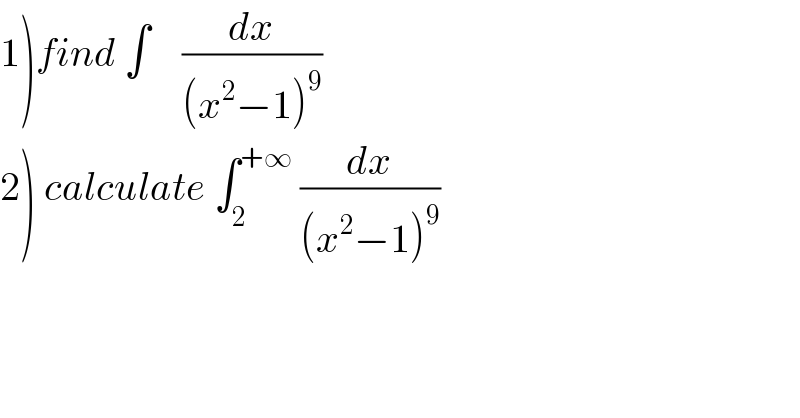 | ||
Commented by mathmax by abdo last updated on 26/Feb/20 | ||
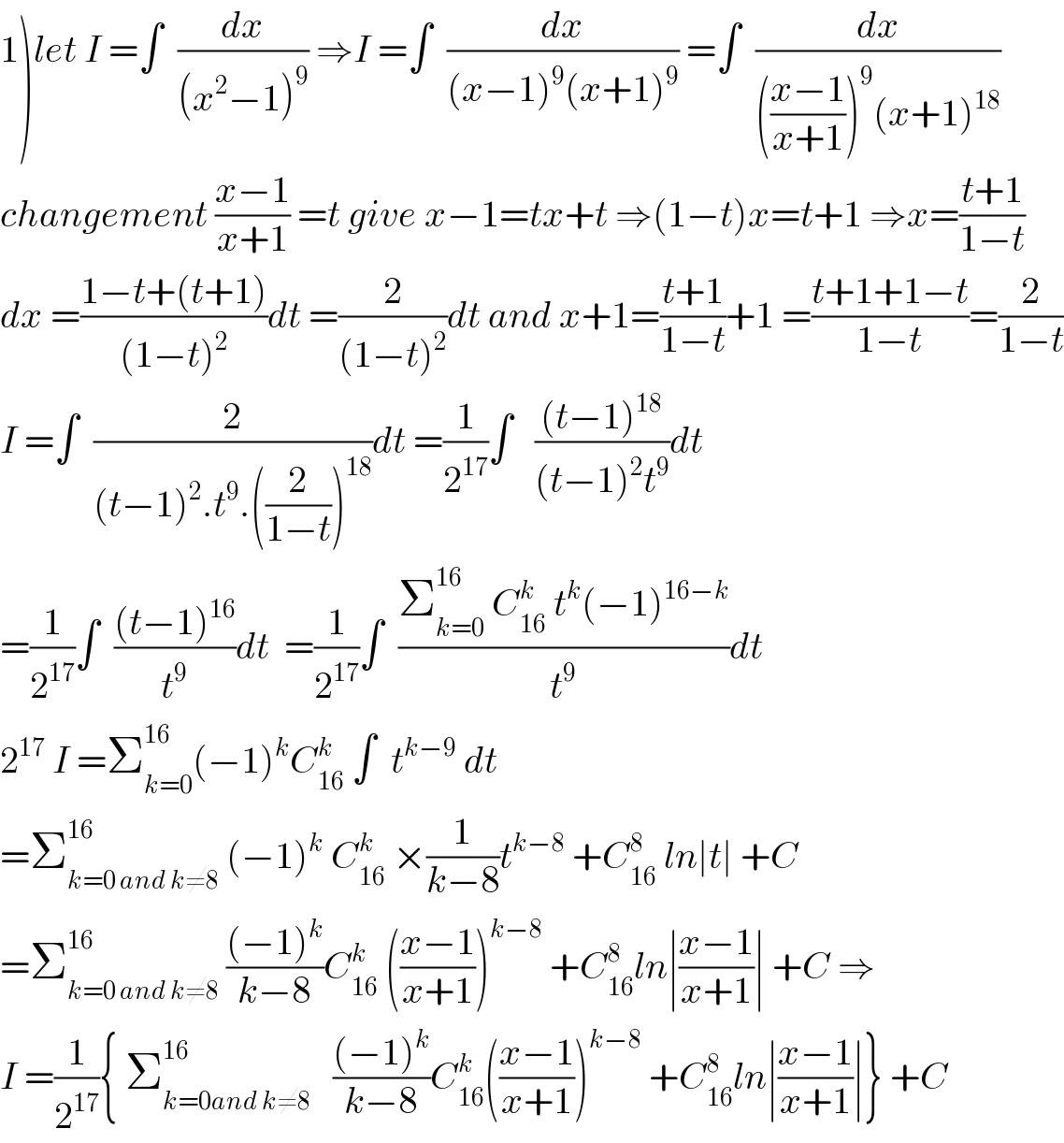 | ||
Commented by mathmax by abdo last updated on 26/Feb/20 | ||
![2) ∫_2 ^(+∞) (dx/((x^2 −1)^9 ))=(1/2^(17) )[Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k (((x−1)/(x+1)))^(k−8) +C_(16) ^8 ln∣((x−1)/(x+1))∣]_2 ^(+∞) =(1/2^(17) ){Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k −Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k ((1/3))^(k−8) −C_(16) ^8 ln((1/3))} =(1/2^(17) )Σ_(k=0 and k≠8) ^(16) (((−1)^k )/(k−8))C_(16) ^k (1−(1/3^(k−8) ))+(C_(16) ^8 /2^(17) )ln(3)](Q83006.png) | ||