Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 83144 by M±th+et£s last updated on 28/Feb/20

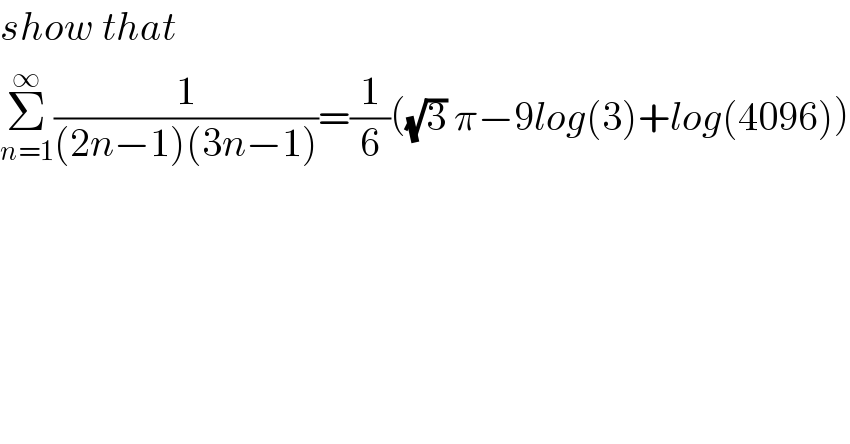
show that Σ_(n=1) ^∞ (1/((2n−1)(3n−1)))=(1/6)((√3) π−9log(3)+log(4096))

$${show}\:{that} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{3}{n}−\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{6}}\left(\sqrt{\mathrm{3}}\:\pi−\mathrm{9}{log}\left(\mathrm{3}\right)+{log}\left(\mathrm{4096}\right)\right) \\ $$

Answered by mind is power last updated on 28/Feb/20

=(1/6)Σ_(n=1) ^(+∞) (1/((n−(1/2))(n−(1/3)))) =(1/6)Σ_(n=0) ^(+∞) (1/((n+(1/2))(n+(2/3))))=(1/6).((Ψ((2/3))−Ψ((1/2)))/((2/3)−(1/2))) Ψ((2/3))=−γ−ln(6)−(π/2)cot(((2π)/3))+2cos(((4π)/3))ln(sin(π/3)) Ψ((1/2))=−γ−ln(4) Ψ((2/3))−Ψ((1/2))=ln((2/3))+(π/(2(√3)))−ln(((√3)/2)) ((Ψ((2/3))−Ψ((1/2)))/((2/3)−(1/2)))=6(Ψ((2/3))−Ψ((1/2)))=6((π/(2(√3)))+ln(2)−ln(3)−(1/2)ln(3)+ln(2)) =π(√3)+ln(2^(12) )−3ln(3)=π(√3)+ln(4096)−9ln(3) Σ_(n=1) ^(+∞) (1/((2n−1)(3n−1)))=(1/6).(π(√3)−9ln(3)+ln(4096))

$$=\frac{\mathrm{1}}{\mathrm{6}}\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({n}−\frac{\mathrm{1}}{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)}=\frac{\mathrm{1}}{\mathrm{6}}.\frac{\Psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)=−\gamma−{ln}\left(\mathrm{6}\right)−\frac{\pi}{\mathrm{2}}{cot}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)+\mathrm{2}{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{3}}\right){ln}\left({sin}\frac{\pi}{\mathrm{3}}\right) \\ $$$$\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\gamma−{ln}\left(\mathrm{4}\right) \\ $$$$\Psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)={ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}−{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\frac{\Psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{6}\left(\Psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)=\mathrm{6}\left(\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}+{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)+{ln}\left(\mathrm{2}\right)\right) \\ $$$$=\pi\sqrt{\mathrm{3}}+{ln}\left(\mathrm{2}^{\mathrm{12}} \right)−\mathrm{3}{ln}\left(\mathrm{3}\right)=\pi\sqrt{\mathrm{3}}+{ln}\left(\mathrm{4096}\right)−\mathrm{9}{ln}\left(\mathrm{3}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{3}{n}−\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{6}}.\left(\pi\sqrt{\mathrm{3}}−\mathrm{9}{ln}\left(\mathrm{3}\right)+{ln}\left(\mathrm{4096}\right)\right) \\ $$$$ \\ $$

Commented by mind is power last updated on 28/Feb/20

Ψ((p/q))=−γ−ln(2q)−(π/2)cot(((pπ)/q))+2Σ_(n=1) ^([((q−1)/2)]) cos(((2πnp)/q))ln(sin((πn)/q))

$$\Psi\left(\frac{{p}}{{q}}\right)=−\gamma−{ln}\left(\mathrm{2}{q}\right)−\frac{\pi}{\mathrm{2}}{cot}\left(\frac{{p}\pi}{{q}}\right)+\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\left[\frac{{q}−\mathrm{1}}{\mathrm{2}}\right]} {\sum}}{cos}\left(\frac{\mathrm{2}\pi{np}}{{q}}\right){ln}\left({sin}\frac{\pi{n}}{{q}}\right) \\ $$$$ \\ $$

Commented by M±th+et£s last updated on 28/Feb/20

god bless you sir

$${god}\:{bless}\:{you}\:{sir} \\ $$

Commented by msup trace by abdo last updated on 28/Feb/20

define Φ sir mind....

$${define}\:\Phi\:{sir}\:{mind}.... \\ $$

Commented by mathmax by abdo last updated on 28/Feb/20

thank you sir mind

$${thank}\:{you}\:{sir}\:{mind} \\ $$

Commented by mind is power last updated on 28/Feb/20

withe pleasur sir

$${withe}\:{pleasur}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com