
Question and Answers Forum
Question Number 83146 by 09658867628 last updated on 28/Feb/20
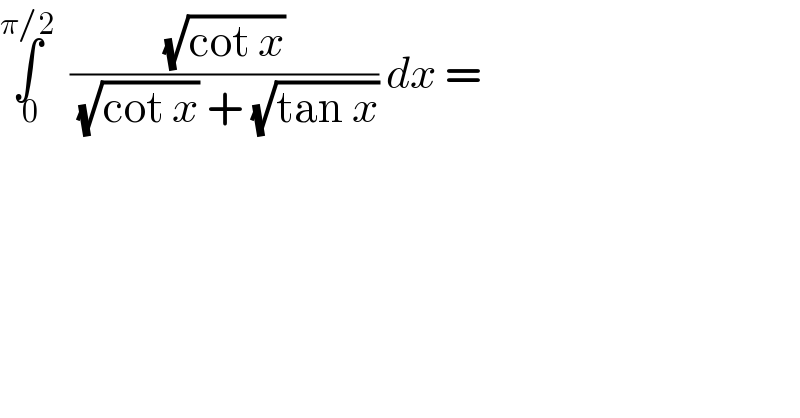
Answered by Kunal12588 last updated on 28/Feb/20

Answered by niroj last updated on 28/Feb/20
![let, I= ∫_0 ^(π/2) (( (√(cot x)))/( (√(cot x)) +(√(tan x))))dx.....(i) = ∫_0 ^(π/2) ((√( cot ((π/2)−x)))/( (√(cot ((π/2))) −x)+ (√(tan ((π/2) −x)))))dx ∵ ∫_0 ^( a) xdx=∫_0 ^a (a−x)dx = ∫_0 ^( (π/2)) ((√(tan x))/( (√(tan x)) +(√(cot x))))dx......(ii) added (i)&(ii) 2I= ∫_0 ^(π/2) ( (( (√(cot x)))/( (√(cot x)) +(√(tan x)))) + ((√(tan x))/( (√(tan x)) +(√(cot x)))))dx 2I= ∫_0 ^( (π/2)) ((( (√(cot x)) +(√(tan x)))/( (√(cot x))+(√(tan x)))))dx 2I= ∫_0 ^(π/2) dx 2I= [ x]_0 ^(π/2) 2I= ((π/2)−0) 2I= (π/2) ⇒ I= (π/4) //.](Q83151.png)
Commented by peter frank last updated on 28/Feb/20
| ||
Question and Answers Forum | ||
Question Number 83146 by 09658867628 last updated on 28/Feb/20 | ||
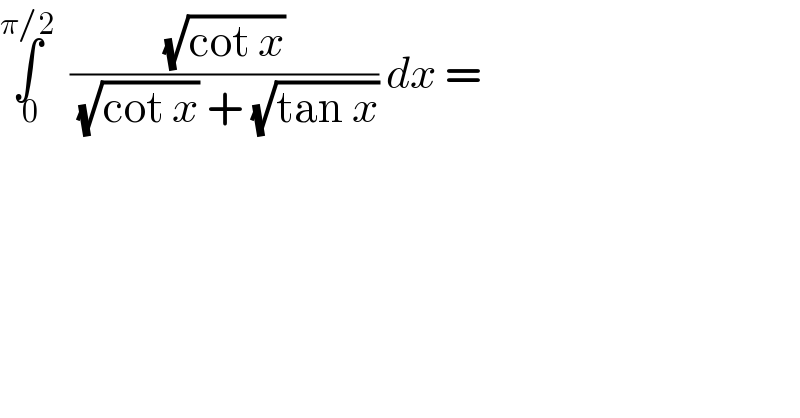 | ||
Answered by Kunal12588 last updated on 28/Feb/20 | ||
 | ||
| ||
Answered by niroj last updated on 28/Feb/20 | ||
![let, I= ∫_0 ^(π/2) (( (√(cot x)))/( (√(cot x)) +(√(tan x))))dx.....(i) = ∫_0 ^(π/2) ((√( cot ((π/2)−x)))/( (√(cot ((π/2))) −x)+ (√(tan ((π/2) −x)))))dx ∵ ∫_0 ^( a) xdx=∫_0 ^a (a−x)dx = ∫_0 ^( (π/2)) ((√(tan x))/( (√(tan x)) +(√(cot x))))dx......(ii) added (i)&(ii) 2I= ∫_0 ^(π/2) ( (( (√(cot x)))/( (√(cot x)) +(√(tan x)))) + ((√(tan x))/( (√(tan x)) +(√(cot x)))))dx 2I= ∫_0 ^( (π/2)) ((( (√(cot x)) +(√(tan x)))/( (√(cot x))+(√(tan x)))))dx 2I= ∫_0 ^(π/2) dx 2I= [ x]_0 ^(π/2) 2I= ((π/2)−0) 2I= (π/2) ⇒ I= (π/4) //.](Q83151.png) | ||
| ||
Commented by peter frank last updated on 28/Feb/20 | ||
 | ||