Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 84242 by Rio Michael last updated on 10/Mar/20

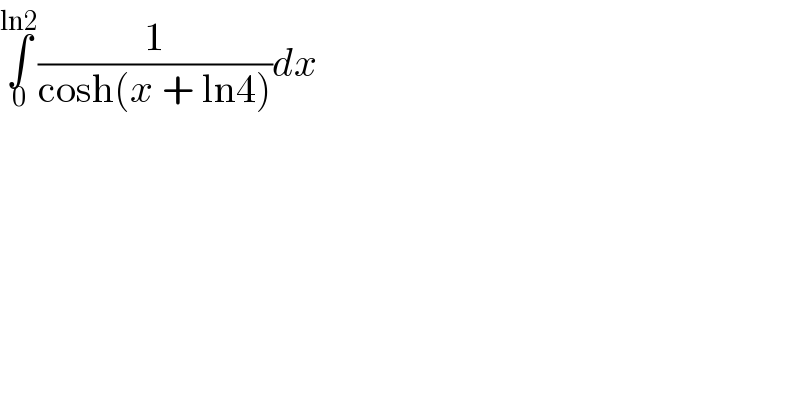
∫_0 ^(ln2) (1/(cosh(x + ln4)))dx

$$\underset{\mathrm{0}} {\overset{\mathrm{ln2}} {\int}}\frac{\mathrm{1}}{\mathrm{cosh}\left({x}\:+\:\mathrm{ln4}\right)}{dx} \\ $$

Commented by mathmax by abdo last updated on 10/Mar/20

I =∫_0 ^(ln(2)) (1/(ch(x+ln4)))dx ⇒I =_(x+ln4=t) ∫_(2ln(2)) ^(3ln(2)) (dt/(ch(t))) =2 ∫_(2ln(2)) ^(3ln(2)) (dt/(e^t +e^(−t) )) =_(e^t =u) 2 ∫_4 ^8 (du/(u(u+u^(−1) ))) =2∫_4 ^8 (du/(u^2 +1)) =2[arctanu]_4 ^8 =2(arctan(8)−arctan(4))

$${I}\:=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \:\frac{\mathrm{1}}{{ch}\left({x}+{ln}\mathrm{4}\right)}{dx}\:\Rightarrow{I}\:=_{{x}+{ln}\mathrm{4}={t}} \:\:\int_{\mathrm{2}{ln}\left(\mathrm{2}\right)} ^{\mathrm{3}{ln}\left(\mathrm{2}\right)} \:\:\frac{{dt}}{{ch}\left({t}\right)} \\ $$$$=\mathrm{2}\:\int_{\mathrm{2}{ln}\left(\mathrm{2}\right)} ^{\mathrm{3}{ln}\left(\mathrm{2}\right)} \:\frac{{dt}}{{e}^{{t}} \:+{e}^{−{t}} }\:=_{{e}^{{t}} ={u}} \:\:\mathrm{2}\:\int_{\mathrm{4}} ^{\mathrm{8}} \:\frac{{du}}{{u}\left({u}+{u}^{−\mathrm{1}} \right)}\:=\mathrm{2}\int_{\mathrm{4}} ^{\mathrm{8}} \:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\mathrm{2}\left[{arctanu}\right]_{\mathrm{4}} ^{\mathrm{8}} \:=\mathrm{2}\left({arctan}\left(\mathrm{8}\right)−{arctan}\left(\mathrm{4}\right)\right) \\ $$

Answered by TANMAY PANACEA last updated on 10/Mar/20

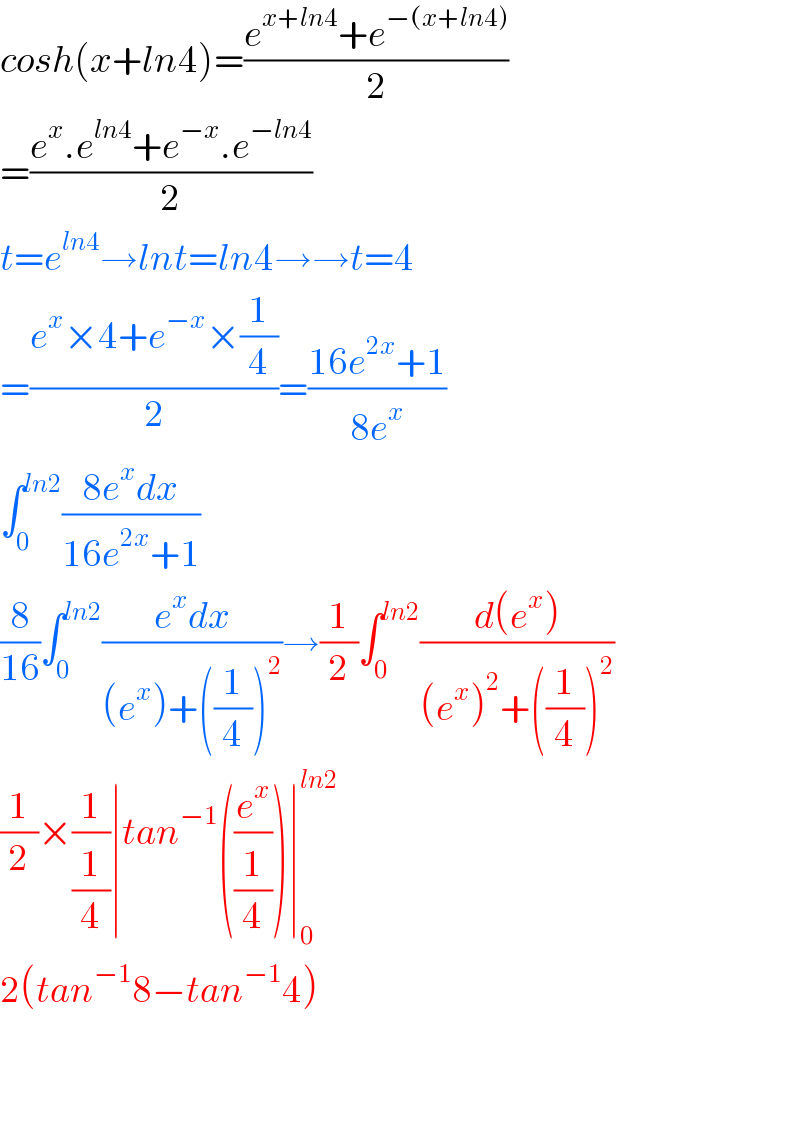
cosh(x+ln4)=((e^(x+ln4) +e^(−(x+ln4)) )/2) =((e^x .e^(ln4) +e^(−x) .e^(−ln4) )/2) t=e^(ln4) →lnt=ln4→→t=4 =((e^x ×4+e^(−x) ×(1/4))/2)=((16e^(2x) +1)/(8e^x )) ∫_0 ^(ln2) ((8e^x dx)/(16e^(2x) +1)) (8/(16))∫_0 ^(ln2) ((e^x dx)/((e^x )+((1/4))^2 ))→(1/2)∫_0 ^(ln2) ((d(e^x ))/((e^x )^2 +((1/4))^2 )) (1/2)×(1/(1/4))∣tan^(−1) ((e^x /(1/4)))∣_0 ^(ln2) 2(tan^(−1) 8−tan^(−1) 4)

$${cosh}\left({x}+{ln}\mathrm{4}\right)=\frac{{e}^{{x}+{ln}\mathrm{4}} +{e}^{−\left({x}+{ln}\mathrm{4}\right)} }{\mathrm{2}} \\ $$$$=\frac{{e}^{{x}} .{e}^{{ln}\mathrm{4}} +{e}^{−{x}} .{e}^{−{ln}\mathrm{4}} }{\mathrm{2}} \\ $$$${t}={e}^{{ln}\mathrm{4}} \rightarrow{lnt}={ln}\mathrm{4}\rightarrow\rightarrow{t}=\mathrm{4} \\ $$$$=\frac{{e}^{{x}} ×\mathrm{4}+{e}^{−{x}} ×\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{16}{e}^{\mathrm{2}{x}} +\mathrm{1}}{\mathrm{8}{e}^{{x}} } \\ $$$$\int_{\mathrm{0}} ^{{ln}\mathrm{2}} \frac{\mathrm{8}{e}^{{x}} {dx}}{\mathrm{16}{e}^{\mathrm{2}{x}} +\mathrm{1}} \\ $$$$\frac{\mathrm{8}}{\mathrm{16}}\int_{\mathrm{0}} ^{{ln}\mathrm{2}} \frac{{e}^{{x}} {dx}}{\left({e}^{{x}} \right)+\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }\rightarrow\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{ln}\mathrm{2}} \frac{{d}\left({e}^{{x}} \right)}{\left({e}^{{x}} \right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{4}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{e}^{{x}} }{\frac{\mathrm{1}}{\mathrm{4}}}\right)\mid_{\mathrm{0}} ^{{ln}\mathrm{2}} \\ $$$$\mathrm{2}\left({tan}^{−\mathrm{1}} \mathrm{8}−{tan}^{−\mathrm{1}} \mathrm{4}\right) \\ $$$$ \\ $$$$ \\ $$

Commented by Rio Michael last updated on 10/Mar/20

thanks

$$\mathrm{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com