
Question and Answers Forum
Question Number 83206 by mathmax by abdo last updated on 28/Feb/20
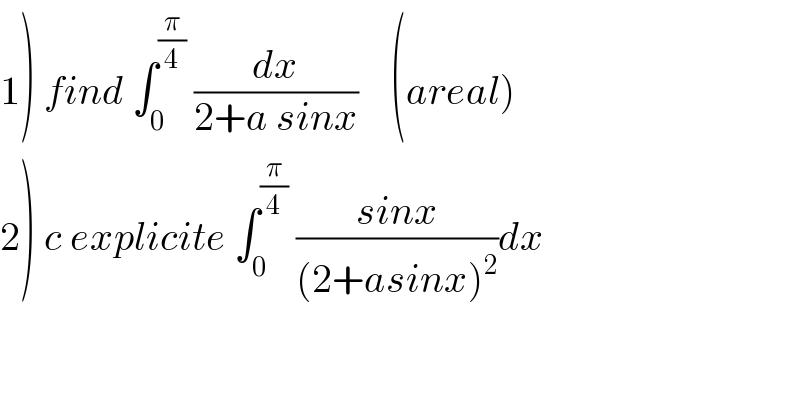
Commented by mathmax by abdo last updated on 29/Feb/20
![1) let f(a)=∫_0 ^(π/4) (dx/(2+asinx)) changement tan((x/2))=t give f(a) =∫_0 ^((√2)−1) ((2dt)/((1+t^2 )(2+a((2t)/(1+t^2 ))))) =2∫_0 ^((√2)−1) (dt/(2+2t^2 +2at)) =∫_0 ^((√2)−1) (dt/(t^2 +at +1)) t^2 +at+1=0→Δ=a^2 −4 if ∣a∣>2 ⇒ Δ>0 ⇒t_1 =((−a+(√(a^2 −4)))/2) and t_2 =((−a−(√(a^2 −4)))/2) ⇒f(a) =∫_0 ^((√2)−1) (dt/((t−t_1 )(t−t_2 ))) =(1/(t−t_2 ))∫_0 ^((√2)−1) ((1/(t−t_1 ))−(1/(t−t_2 )))dt =(1/(√(a^2 −4))) [ln∣((t−t_1 )/(t−t_2 ))∣]_0 ^((√2)−1) =(1/(√(a^2 −4))){ln∣(((√2)−1−((−a+(√(a^2 −4)))/2))/((√2)−1−((−a−(√(a^2 −4)))/2)))∣ −ln∣((−a+(√(a^2 −4)))/(−a−(√(a^2 −4))))∣}=(1/(√(a^2 −4))){ln∣((2(√2)−2+a−(√(a^2 −4)))/(2(√2)−2+a+(√(a^2 −4))))∣ −ln∣((a−(√(a^2 −4)))/(a+(√(a^2 −4))))∣ if ∣a∣<2 ⇒Δ<0 ⇒f(a)=∫_0 ^((√2)−1) (dt/(t^2 +((2at)/2) +(a^2 /4)+1−(a^2 /4))) =∫_0 ^((√2)−1) (dt/((t+(a/2))^2 +((4−a^2 )/4))) =_(t+(a/2)=((√(4−a^2 ))/2)u→u=((2t+a)/(√(4−a^2 )))) (4/(4−a^2 )) ∫_(a/(√(4−a^2 ))) ^((2(√2)−2+a)/(√(4−a^2 ))) (1/(1+u^2 ))×((√(4−a^2 ))/2)du =(2/(√(4−a^2 )))[arctanu]_(a/(√(4−a^2 ))) ^((2(√2)−2+a)/(√(4−a^2 ))) =(2/(√(4−a^2 ))){ arctan(((2(√2)−2+a)/(√(4−a^2 )))) −arctan((a/(√(4−a^2 ))))}](Q83299.png)
Commented by mathmax by abdo last updated on 29/Feb/20
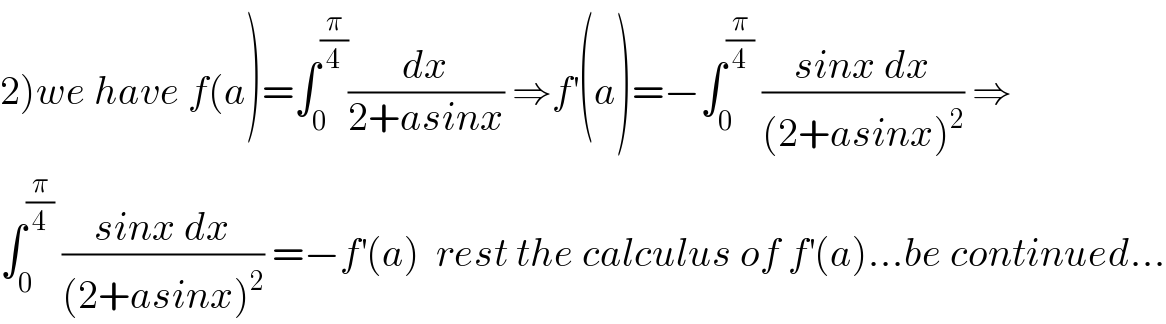
| ||
Question and Answers Forum | ||
Question Number 83206 by mathmax by abdo last updated on 28/Feb/20 | ||
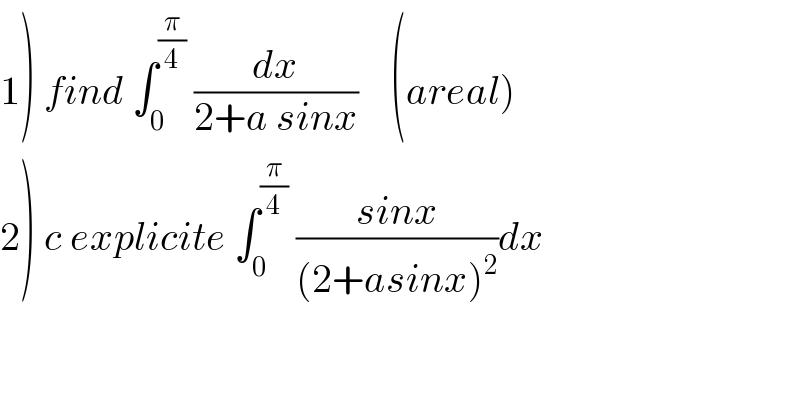 | ||
Commented by mathmax by abdo last updated on 29/Feb/20 | ||
![1) let f(a)=∫_0 ^(π/4) (dx/(2+asinx)) changement tan((x/2))=t give f(a) =∫_0 ^((√2)−1) ((2dt)/((1+t^2 )(2+a((2t)/(1+t^2 ))))) =2∫_0 ^((√2)−1) (dt/(2+2t^2 +2at)) =∫_0 ^((√2)−1) (dt/(t^2 +at +1)) t^2 +at+1=0→Δ=a^2 −4 if ∣a∣>2 ⇒ Δ>0 ⇒t_1 =((−a+(√(a^2 −4)))/2) and t_2 =((−a−(√(a^2 −4)))/2) ⇒f(a) =∫_0 ^((√2)−1) (dt/((t−t_1 )(t−t_2 ))) =(1/(t−t_2 ))∫_0 ^((√2)−1) ((1/(t−t_1 ))−(1/(t−t_2 )))dt =(1/(√(a^2 −4))) [ln∣((t−t_1 )/(t−t_2 ))∣]_0 ^((√2)−1) =(1/(√(a^2 −4))){ln∣(((√2)−1−((−a+(√(a^2 −4)))/2))/((√2)−1−((−a−(√(a^2 −4)))/2)))∣ −ln∣((−a+(√(a^2 −4)))/(−a−(√(a^2 −4))))∣}=(1/(√(a^2 −4))){ln∣((2(√2)−2+a−(√(a^2 −4)))/(2(√2)−2+a+(√(a^2 −4))))∣ −ln∣((a−(√(a^2 −4)))/(a+(√(a^2 −4))))∣ if ∣a∣<2 ⇒Δ<0 ⇒f(a)=∫_0 ^((√2)−1) (dt/(t^2 +((2at)/2) +(a^2 /4)+1−(a^2 /4))) =∫_0 ^((√2)−1) (dt/((t+(a/2))^2 +((4−a^2 )/4))) =_(t+(a/2)=((√(4−a^2 ))/2)u→u=((2t+a)/(√(4−a^2 )))) (4/(4−a^2 )) ∫_(a/(√(4−a^2 ))) ^((2(√2)−2+a)/(√(4−a^2 ))) (1/(1+u^2 ))×((√(4−a^2 ))/2)du =(2/(√(4−a^2 )))[arctanu]_(a/(√(4−a^2 ))) ^((2(√2)−2+a)/(√(4−a^2 ))) =(2/(√(4−a^2 ))){ arctan(((2(√2)−2+a)/(√(4−a^2 )))) −arctan((a/(√(4−a^2 ))))}](Q83299.png) | ||
Commented by mathmax by abdo last updated on 29/Feb/20 | ||
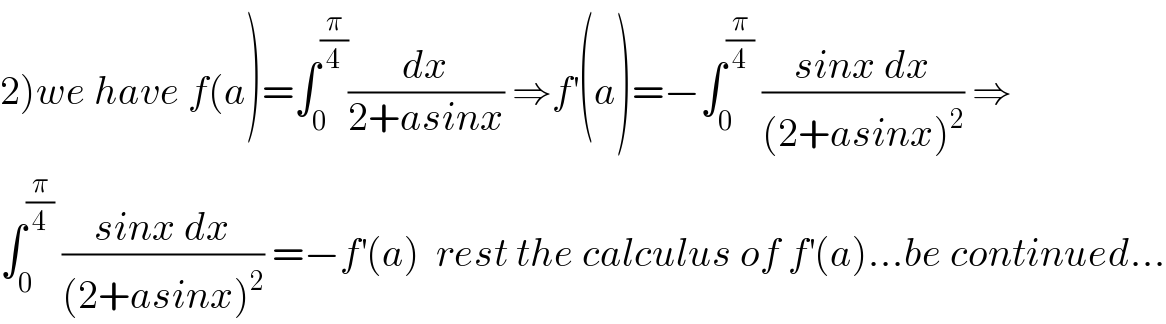 | ||