
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 83327 by john santu last updated on 01/Mar/20
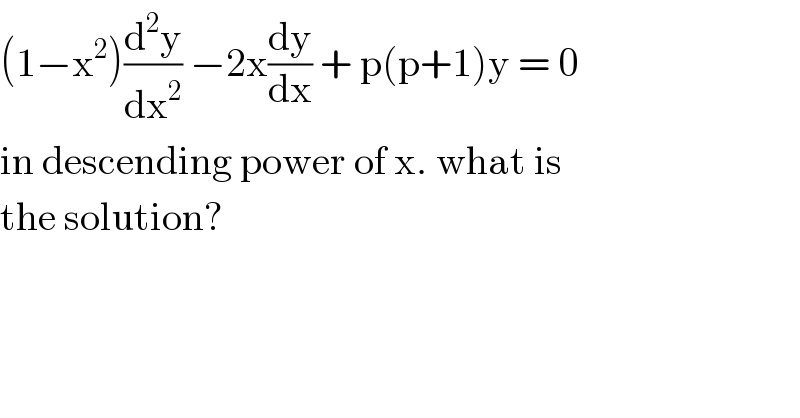
Commented by Joel578 last updated on 01/Mar/20

Commented by niroj last updated on 01/Mar/20
![(1−x^2 )(d^2 y/dx^2 )−2x(dy/dx)+p(p+1)y=0....(i) Sol^n : let, x=0 , f(x)≠0 i.e. x=0 is ordinary point i.e. solution of equation is y= Σ_(r=0) ^∞ a_r x^r (dy/dx)= Σ_(r=0) ^∞ a_r rx^(r−1) (d^2 y/dx^2 ) = Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) Put, the value of y,y_1 and y_2 in eq^n (i) (1−x^2 )Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −2xΣ_(r=0) ^∞ a_r rx^(r−1) +p(p+1)Σ_(r=0) ^∞ a_r x^r =0 or, Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −Σ_(r=0) ^∞ a_r r(r−1)x^r −2Σ_(r=0) ^∞ a_r rx^r +p(p+1)Σ_(r=0) ^∞ a_r x^r =0 or, Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −Σ_(r=0) ^∞ a_r [r(r−1)+2r−p(p+1)]x^r =0 or_, Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −Σ_(r=0) ^∞ a_r [r^2 +r−p(p+1)]x^r =0 or_(, ) Σ_(r=0) ^∞ a_r [(r^2 −r)x^(r−2) −(r^2 +r−p^2 −p)]x^r =0 or,a_r r(r−1)x^(r−2) −a_r [r(r+1)−p(p+1)]x^r =0 put r=r+2 a_(r+2) (r+2)(r+1)x^r −a_r [(r+2)(r+3)−p(p+1)]x^r =0 or, [a_(r+2) (r+2)(r+1)−a_r {(r+2)(r+3)−p(p+1)}]x^r =0 or, a_(r+2) (r+2)(r+1)−a_r {(r+2)(r+3)−p(p+1)}=0 a_(r+2) = (((r+2)(r+3)−p(p+1))/((r+2)(r+1)))a_r put r=0, a_2 = ((2.3−p(p+1))/(2.1))a_0 then put descending value of r in terms of power series y= Σ_(r=0) ^∞ a_r x^r = a_0 +ax+a_2 x^2 +....](Q83384.png)
| ||
Question and Answers Forum | ||
Previous in Differential Equation Next in Differential Equation | ||
Question Number 83327 by john santu last updated on 01/Mar/20 | ||
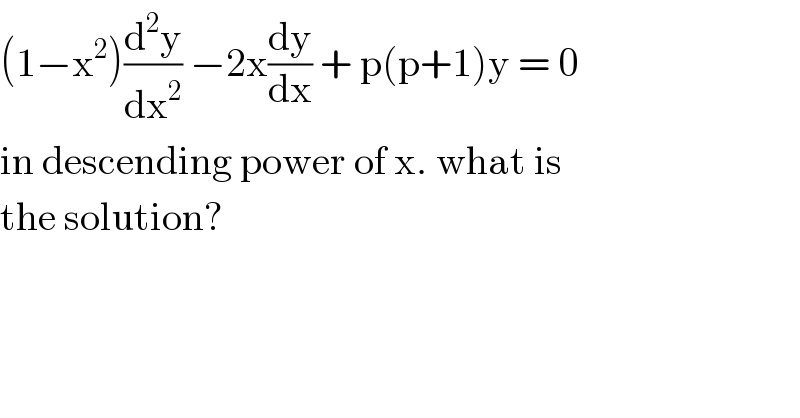 | ||
Commented by Joel578 last updated on 01/Mar/20 | ||
 | ||
Commented by niroj last updated on 01/Mar/20 | ||
![(1−x^2 )(d^2 y/dx^2 )−2x(dy/dx)+p(p+1)y=0....(i) Sol^n : let, x=0 , f(x)≠0 i.e. x=0 is ordinary point i.e. solution of equation is y= Σ_(r=0) ^∞ a_r x^r (dy/dx)= Σ_(r=0) ^∞ a_r rx^(r−1) (d^2 y/dx^2 ) = Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) Put, the value of y,y_1 and y_2 in eq^n (i) (1−x^2 )Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −2xΣ_(r=0) ^∞ a_r rx^(r−1) +p(p+1)Σ_(r=0) ^∞ a_r x^r =0 or, Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −Σ_(r=0) ^∞ a_r r(r−1)x^r −2Σ_(r=0) ^∞ a_r rx^r +p(p+1)Σ_(r=0) ^∞ a_r x^r =0 or, Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −Σ_(r=0) ^∞ a_r [r(r−1)+2r−p(p+1)]x^r =0 or_, Σ_(r=0) ^∞ a_r r(r−1)x^(r−2) −Σ_(r=0) ^∞ a_r [r^2 +r−p(p+1)]x^r =0 or_(, ) Σ_(r=0) ^∞ a_r [(r^2 −r)x^(r−2) −(r^2 +r−p^2 −p)]x^r =0 or,a_r r(r−1)x^(r−2) −a_r [r(r+1)−p(p+1)]x^r =0 put r=r+2 a_(r+2) (r+2)(r+1)x^r −a_r [(r+2)(r+3)−p(p+1)]x^r =0 or, [a_(r+2) (r+2)(r+1)−a_r {(r+2)(r+3)−p(p+1)}]x^r =0 or, a_(r+2) (r+2)(r+1)−a_r {(r+2)(r+3)−p(p+1)}=0 a_(r+2) = (((r+2)(r+3)−p(p+1))/((r+2)(r+1)))a_r put r=0, a_2 = ((2.3−p(p+1))/(2.1))a_0 then put descending value of r in terms of power series y= Σ_(r=0) ^∞ a_r x^r = a_0 +ax+a_2 x^2 +....](Q83384.png) | ||