
Question and Answers Forum
Question Number 83383 by mhmd last updated on 01/Mar/20
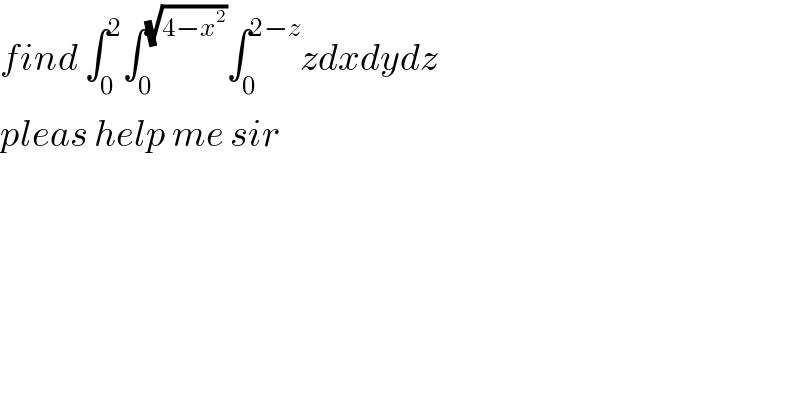
Answered by mr W last updated on 01/Mar/20
![∫_0 ^2 ∫_0 ^(√(4−x^2 )) ∫_0 ^(2−z) zdxdydz =∫_0 ^2 ∫_0 ^(√(4−x^2 )) (∫_0 ^(2−z) zdy)dzdx =∫_0 ^2 (∫_0 ^(√(4−x^2 )) z(2−z)dz)dx =∫_0 ^2 [z^2 −(z^3 /3)]_0 ^(√(4−x^2 )) dx =∫_0 ^2 [4−x^2 −(((4−x^2 )^(3/2) )/3)]dx =4×2−(2^3 /3)−(1/3)∫_0 ^2 (4−x^2 )^(3/2) dx =((16)/3)−(1/3)∫_0 ^2 (4−x^2 )^(3/2) dx =((16)/3)−(1/3)×3π (see below) =((16)/3)−π let x=2 sin θ ∫_0 ^2 (4−x^2 )^(3/2) dx =∫_0 ^(π/2) (4 cos^2 θ)^(3/2) 2 cos θ dθ =16∫_0 ^(π/2) cos^4 θ dθ =4∫_0 ^(π/2) (2 cos^2 θ)^2 dθ =4∫_0 ^(π/2) (1+cos 2θ)^2 dθ =4∫_0 ^(π/2) (1+2 cos 2θ+cos^2 2θ) dθ =4∫_0 ^(π/2) (1+2 cos 2θ+((1+cos 4θ)/2)) dθ =4∫_0 ^(π/2) ((3/2)+2 cos 2θ+((cos 4θ)/2)) dθ =4[(3/2)θ+sin 2θ+((sin 4θ)/8)]_0 ^(π/2) =4×(3/2)×(π/2) =3π](Q83393.png)
| ||
Question and Answers Forum | ||
Question Number 83383 by mhmd last updated on 01/Mar/20 | ||
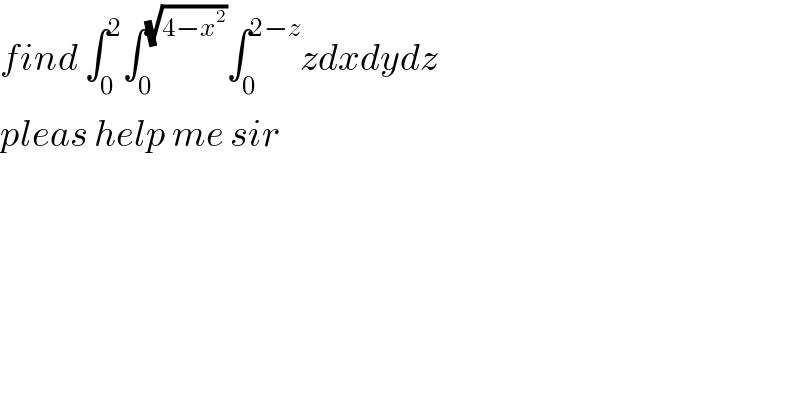 | ||
Answered by mr W last updated on 01/Mar/20 | ||
![∫_0 ^2 ∫_0 ^(√(4−x^2 )) ∫_0 ^(2−z) zdxdydz =∫_0 ^2 ∫_0 ^(√(4−x^2 )) (∫_0 ^(2−z) zdy)dzdx =∫_0 ^2 (∫_0 ^(√(4−x^2 )) z(2−z)dz)dx =∫_0 ^2 [z^2 −(z^3 /3)]_0 ^(√(4−x^2 )) dx =∫_0 ^2 [4−x^2 −(((4−x^2 )^(3/2) )/3)]dx =4×2−(2^3 /3)−(1/3)∫_0 ^2 (4−x^2 )^(3/2) dx =((16)/3)−(1/3)∫_0 ^2 (4−x^2 )^(3/2) dx =((16)/3)−(1/3)×3π (see below) =((16)/3)−π let x=2 sin θ ∫_0 ^2 (4−x^2 )^(3/2) dx =∫_0 ^(π/2) (4 cos^2 θ)^(3/2) 2 cos θ dθ =16∫_0 ^(π/2) cos^4 θ dθ =4∫_0 ^(π/2) (2 cos^2 θ)^2 dθ =4∫_0 ^(π/2) (1+cos 2θ)^2 dθ =4∫_0 ^(π/2) (1+2 cos 2θ+cos^2 2θ) dθ =4∫_0 ^(π/2) (1+2 cos 2θ+((1+cos 4θ)/2)) dθ =4∫_0 ^(π/2) ((3/2)+2 cos 2θ+((cos 4θ)/2)) dθ =4[(3/2)θ+sin 2θ+((sin 4θ)/8)]_0 ^(π/2) =4×(3/2)×(π/2) =3π](Q83393.png) | ||
| ||