Question and Answers Forum
Question Number 83385 by M±th+et£s last updated on 01/Mar/20
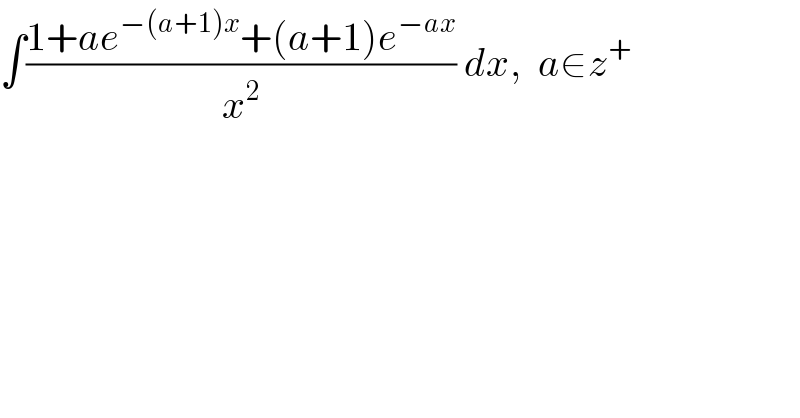
Commented by M±th+et£s last updated on 01/Mar/20

Answered by mind is power last updated on 01/Mar/20
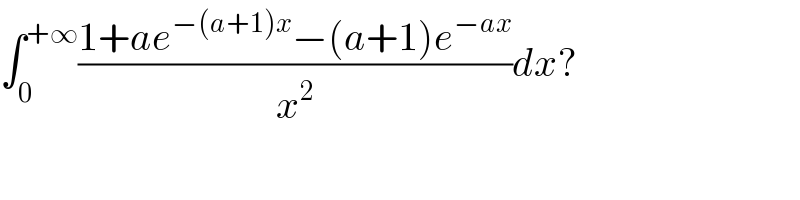
Commented by M±th+et£s last updated on 01/Mar/20

Commented by mathmax by abdo last updated on 02/Mar/20
![by parts u^′ =(1/x^2 ) and v=1+ae^(−(a+1)x) −(a+1)e^(−ax) ⇒ I=[−(1/x)(1+ae^(−(a+1)x) −(a+1)e^(−ax) )]_0 ^(+∞) + ∫_0 ^∞ (e^(−(a+1)x) −a(a+1)e^(−(a+1)x) −e^(−ax) +a(a+1)e^(−ax) )(dx/x) =∫_0 ^∞ ((e^(−(a+1)x) −e^(−ax) )/x)dx −a(a+1)∫_0 ^∞ ((e^(−(a+1)x) −e^(−ax) )/x)dx =(1−a^2 −a)∫_0 ^∞ ((e^(−(a+1)x) −e^(−ax) )/x)dx let ξ(a)=∫_0 ^∞ ((e^(−(a+1)x) −e^(−ax) )/x)dx ⇒ξ^′ (a) =∫_0 ^∞ ((−x e^(−(a+1)x) +xe^(−ax) )/x)dx =∫_0 ^∞ e^(−ax) dx−∫_0 ^∞ e^(−(a+1)x) dx =[−(e^(−ax) /a)]_0 ^∞ −[−(e^(−(a+1)x) /(a+1))]_0 ^(+∞) =(1/a)−(1/(a+1)) ⇒ξ(a) =ln((a/(a+1)))+c (we supoose a>0 ) lim_(a→+∞) ξ(a)=0=c ⇒ξ(a)=ln((a/(a+1))) ⇒I =(1−a^2 −a)ln((a/(a+1))) rest to prove that lim_(x→0) ((1+ae^(−(a+1)x) −(a+1)e^(−ax) )/x) =0 e^(−(a+1)x) ∼1−(a+1)x+(((a+1)x^2 )/2)⇒a e^(−(a+1)x) ∼a−a(a+1)x+((a(a+1)x^2 )/2) e^(−ax) ∼1−ax+((a^2 x^2 )/2) ⇒(a+1)e^(−ax) ∼a+1−a(a+1)x +((a^2 (a+1)x^2 )/2) ⇒ (...−(....)∼1+a−a(a+1)x+((a(a+1)x^2 )/2)−a−1−a(a+1)x−((a^2 (a+1)x^2 )/2) =((a+1)/2)(a−a^2 )x^2 ⇒(((...)−(...))/x)∼ (((a+1)(a−a^2 )x)/2)→0 (x→0)](Q83400.png)
Answered by mind is power last updated on 02/Mar/20
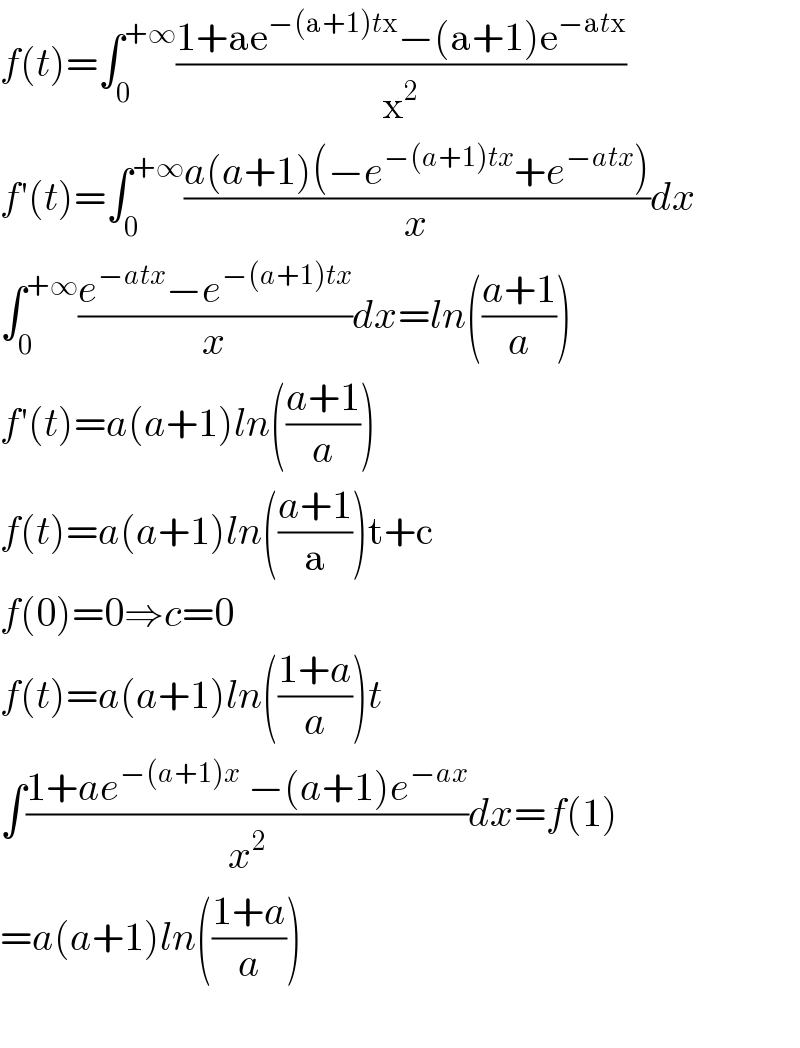
Commented by mind is power last updated on 02/Mar/20
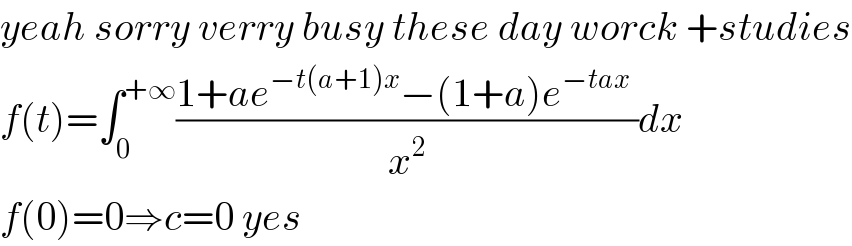
Commented by M±th+et£s last updated on 02/Mar/20
Commented by M±th+et£s last updated on 02/Mar/20
Commented by M±th+et£s last updated on 02/Mar/20

Commented by M±th+et£s last updated on 02/Mar/20