Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 83420 by jagoll last updated on 02/Mar/20

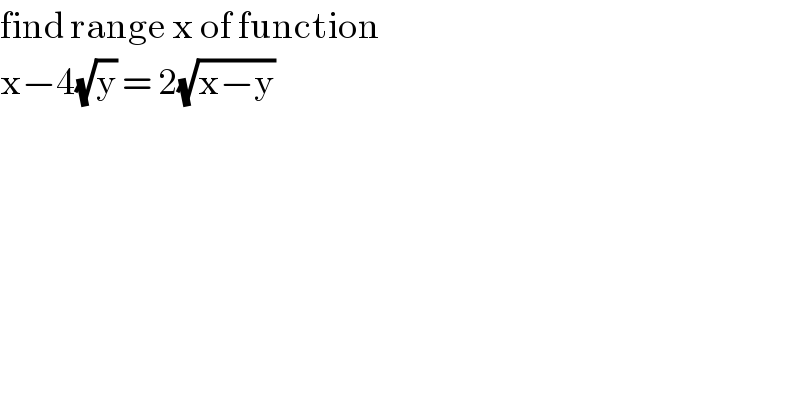
find range x of function x−4(√y) = 2(√(x−y))

$$\mathrm{find}\:\mathrm{range}\:\mathrm{x}\:\mathrm{of}\:\mathrm{function}\: \\ $$$$\mathrm{x}−\mathrm{4}\sqrt{\mathrm{y}}\:=\:\mathrm{2}\sqrt{\mathrm{x}−\mathrm{y}} \\ $$

Commented by mathmax by abdo last updated on 02/Mar/20

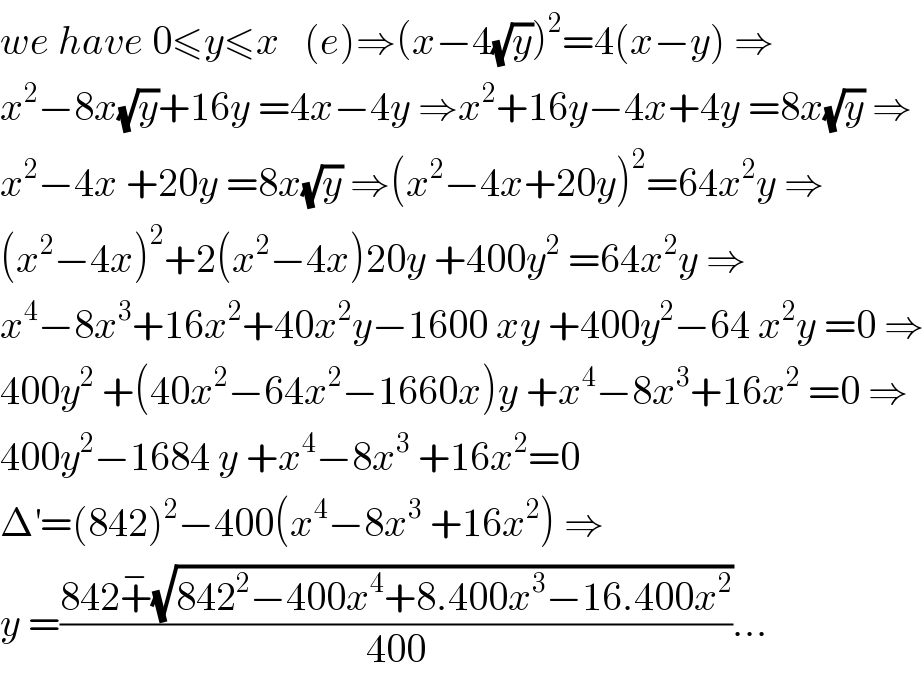
we have 0≤y≤x (e)⇒(x−4(√y))^2 =4(x−y) ⇒ x^2 −8x(√y)+16y =4x−4y ⇒x^2 +16y−4x+4y =8x(√y) ⇒ x^2 −4x +20y =8x(√y) ⇒(x^2 −4x+20y)^2 =64x^2 y ⇒ (x^2 −4x)^2 +2(x^2 −4x)20y +400y^2 =64x^2 y ⇒ x^4 −8x^3 +16x^2 +40x^2 y−1600 xy +400y^2 −64 x^2 y =0 ⇒ 400y^2 +(40x^2 −64x^2 −1660x)y +x^4 −8x^3 +16x^2 =0 ⇒ 400y^2 −1684 y +x^4 −8x^3 +16x^2 =0 Δ^′ =(842)^2 −400(x^4 −8x^3 +16x^2 ) ⇒ y =((842+^− (√(842^2 −400x^4 +8.400x^3 −16.400x^2 )))/(400))...

$${we}\:{have}\:\mathrm{0}\leqslant{y}\leqslant{x}\:\:\:\left({e}\right)\Rightarrow\left({x}−\mathrm{4}\sqrt{{y}}\right)^{\mathrm{2}} =\mathrm{4}\left({x}−{y}\right)\:\Rightarrow \\ $$$${x}^{\mathrm{2}} −\mathrm{8}{x}\sqrt{{y}}+\mathrm{16}{y}\:=\mathrm{4}{x}−\mathrm{4}{y}\:\Rightarrow{x}^{\mathrm{2}} +\mathrm{16}{y}−\mathrm{4}{x}+\mathrm{4}{y}\:=\mathrm{8}{x}\sqrt{{y}}\:\Rightarrow \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{x}\:+\mathrm{20}{y}\:=\mathrm{8}{x}\sqrt{{y}}\:\Rightarrow\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{20}{y}\right)^{\mathrm{2}} =\mathrm{64}{x}^{\mathrm{2}} {y}\:\Rightarrow \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{4}{x}\right)^{\mathrm{2}} +\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{4}{x}\right)\mathrm{20}{y}\:+\mathrm{400}{y}^{\mathrm{2}} \:=\mathrm{64}{x}^{\mathrm{2}} {y}\:\Rightarrow \\ $$$${x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{16}{x}^{\mathrm{2}} +\mathrm{40}{x}^{\mathrm{2}} {y}−\mathrm{1600}\:{xy}\:+\mathrm{400}{y}^{\mathrm{2}} −\mathrm{64}\:{x}^{\mathrm{2}} {y}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{400}{y}^{\mathrm{2}} \:+\left(\mathrm{40}{x}^{\mathrm{2}} −\mathrm{64}{x}^{\mathrm{2}} −\mathrm{1660}{x}\right){y}\:+{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{16}{x}^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{400}{y}^{\mathrm{2}} −\mathrm{1684}\:{y}\:+{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} \:+\mathrm{16}{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Delta^{'} =\left(\mathrm{842}\right)^{\mathrm{2}} −\mathrm{400}\left({x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} \:+\mathrm{16}{x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${y}\:=\frac{\mathrm{842}\overset{−} {+}\sqrt{\mathrm{842}^{\mathrm{2}} −\mathrm{400}{x}^{\mathrm{4}} +\mathrm{8}.\mathrm{400}{x}^{\mathrm{3}} −\mathrm{16}.\mathrm{400}{x}^{\mathrm{2}} }}{\mathrm{400}}... \\ $$

Commented by mr W last updated on 02/Mar/20

to jagoll sir: it′s wrong! x^2 −(4t+16)x+20t^2 = 0 is not a quadratic equation for x! because t contains x!

$${to}\:{jagoll}\:{sir}: \\ $$$${it}'{s}\:{wrong}! \\ $$$$\mathrm{x}^{\mathrm{2}} −\left(\mathrm{4t}+\mathrm{16}\right)\mathrm{x}+\mathrm{20t}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$${is}\:{not}\:{a}\:{quadratic}\:{equation}\:{for}\:{x}! \\ $$$${because}\:{t}\:{contains}\:{x}! \\ $$

Commented by MJS last updated on 02/Mar/20

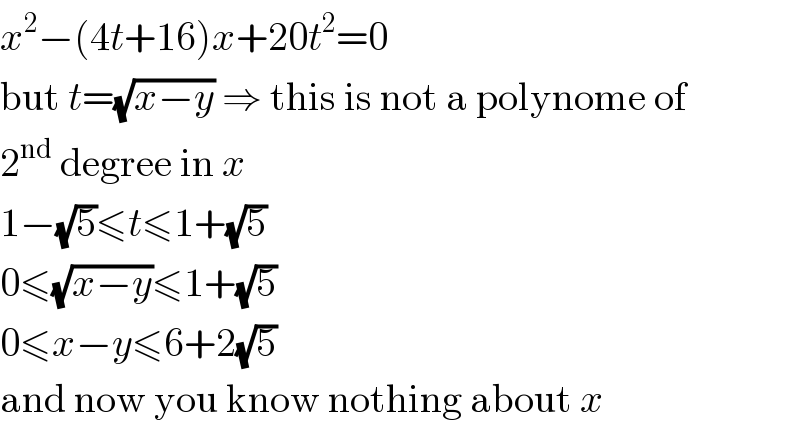
x^2 −(4t+16)x+20t^2 =0 but t=(√(x−y)) ⇒ this is not a polynome of 2^(nd) degree in x 1−(√5)≤t≤1+(√5) 0≤(√(x−y))≤1+(√5) 0≤x−y≤6+2(√5) and now you know nothing about x

$${x}^{\mathrm{2}} −\left(\mathrm{4}{t}+\mathrm{16}\right){x}+\mathrm{20}{t}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{but}\:{t}=\sqrt{{x}−{y}}\:\Rightarrow\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of} \\ $$$$\mathrm{2}^{\mathrm{nd}} \:\mathrm{degree}\:\mathrm{in}\:{x} \\ $$$$\mathrm{1}−\sqrt{\mathrm{5}}\leqslant{t}\leqslant\mathrm{1}+\sqrt{\mathrm{5}} \\ $$$$\mathrm{0}\leqslant\sqrt{{x}−{y}}\leqslant\mathrm{1}+\sqrt{\mathrm{5}} \\ $$$$\mathrm{0}\leqslant{x}−{y}\leqslant\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\mathrm{and}\:\mathrm{now}\:\mathrm{you}\:\mathrm{know}\:\mathrm{nothing}\:\mathrm{about}\:{x} \\ $$

Commented by jagoll last updated on 02/Mar/20

oo yes. i understand now. thank you mister w and mister mjs

$$\mathrm{oo}\:\mathrm{yes}.\:\mathrm{i}\:\mathrm{understand}\:\mathrm{now}.\:\mathrm{thank}\:\mathrm{you} \\ $$$$\mathrm{mister}\:\mathrm{w}\:\mathrm{and}\:\mathrm{mister}\:\mathrm{mjs} \\ $$

Answered by mr W last updated on 02/Mar/20

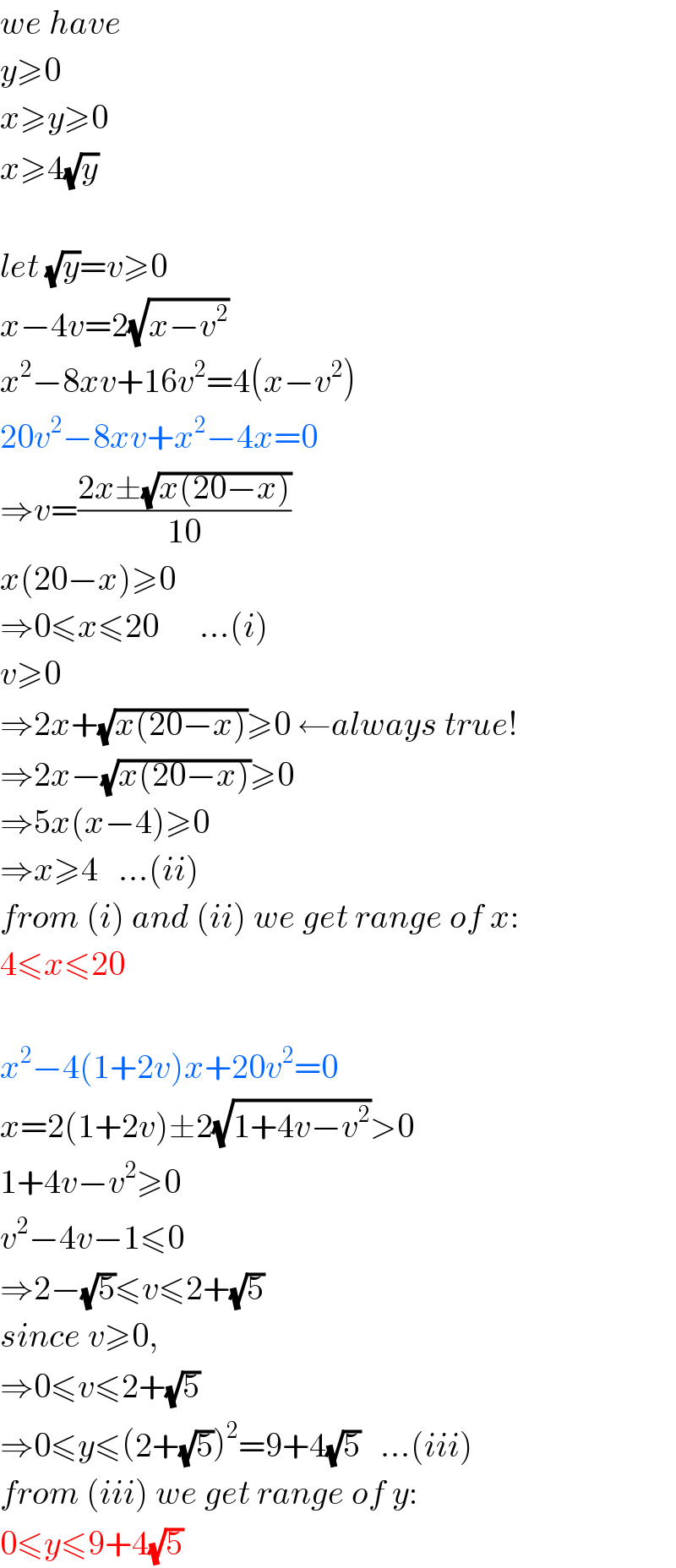
we have y≥0 x≥y≥0 x≥4(√y) let (√y)=v≥0 x−4v=2(√(x−v^2 )) x^2 −8xv+16v^2 =4(x−v^2 ) 20v^2 −8xv+x^2 −4x=0 ⇒v=((2x±(√(x(20−x))))/(10)) x(20−x)≥0 ⇒0≤x≤20 ...(i) v≥0 ⇒2x+(√(x(20−x)))≥0 ←always true! ⇒2x−(√(x(20−x)))≥0 ⇒5x(x−4)≥0 ⇒x≥4 ...(ii) from (i) and (ii) we get range of x: 4≤x≤20 x^2 −4(1+2v)x+20v^2 =0 x=2(1+2v)±2(√(1+4v−v^2 ))>0 1+4v−v^2 ≥0 v^2 −4v−1≤0 ⇒2−(√5)≤v≤2+(√5) since v≥0, ⇒0≤v≤2+(√5) ⇒0≤y≤(2+(√5))^2 =9+4(√5) ...(iii) from (iii) we get range of y: 0≤y≤9+4(√5)

$${we}\:{have} \\ $$$${y}\geqslant\mathrm{0} \\ $$$${x}\geqslant{y}\geqslant\mathrm{0} \\ $$$${x}\geqslant\mathrm{4}\sqrt{{y}} \\ $$$$ \\ $$$${let}\:\sqrt{{y}}={v}\geqslant\mathrm{0} \\ $$$${x}−\mathrm{4}{v}=\mathrm{2}\sqrt{{x}−{v}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} −\mathrm{8}{xv}+\mathrm{16}{v}^{\mathrm{2}} =\mathrm{4}\left({x}−{v}^{\mathrm{2}} \right) \\ $$$$\mathrm{20}{v}^{\mathrm{2}} −\mathrm{8}{xv}+{x}^{\mathrm{2}} −\mathrm{4}{x}=\mathrm{0} \\ $$$$\Rightarrow{v}=\frac{\mathrm{2}{x}\pm\sqrt{{x}\left(\mathrm{20}−{x}\right)}}{\mathrm{10}} \\ $$$${x}\left(\mathrm{20}−{x}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{0}\leqslant{x}\leqslant\mathrm{20}\:\:\:\:\:\:...\left({i}\right) \\ $$$${v}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{x}+\sqrt{{x}\left(\mathrm{20}−{x}\right)}\geqslant\mathrm{0}\:\leftarrow{always}\:{true}! \\ $$$$\Rightarrow\mathrm{2}{x}−\sqrt{{x}\left(\mathrm{20}−{x}\right)}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}{x}\left({x}−\mathrm{4}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow{x}\geqslant\mathrm{4}\:\:\:...\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{get}\:{range}\:{of}\:{x}: \\ $$$$\mathrm{4}\leqslant{x}\leqslant\mathrm{20} \\ $$$$ \\ $$$${x}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}+\mathrm{2}{v}\right){x}+\mathrm{20}{v}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\mathrm{2}\left(\mathrm{1}+\mathrm{2}{v}\right)\pm\mathrm{2}\sqrt{\mathrm{1}+\mathrm{4}{v}−{v}^{\mathrm{2}} }>\mathrm{0} \\ $$$$\mathrm{1}+\mathrm{4}{v}−{v}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$${v}^{\mathrm{2}} −\mathrm{4}{v}−\mathrm{1}\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}−\sqrt{\mathrm{5}}\leqslant{v}\leqslant\mathrm{2}+\sqrt{\mathrm{5}} \\ $$$${since}\:{v}\geqslant\mathrm{0}, \\ $$$$\Rightarrow\mathrm{0}\leqslant{v}\leqslant\mathrm{2}+\sqrt{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{0}\leqslant{y}\leqslant\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} =\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}\:\:\:...\left({iii}\right) \\ $$$${from}\:\left({iii}\right)\:{we}\:{get}\:{range}\:{of}\:{y}: \\ $$$$\mathrm{0}\leqslant{y}\leqslant\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com