Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 83445 by naka3546 last updated on 02/Mar/20

The nearest distance of (0, 3) to curve : y = 6 − x^2 is ...

$${The}\:\:{nearest}\:\:{distance}\:\:{of}\:\:\left(\mathrm{0},\:\mathrm{3}\right)\:\:{to}\:\:{curve}\:\::\:\:{y}\:=\:\:\mathrm{6}\:−\:{x}^{\mathrm{2}} \:\:{is}\:\:... \\ $$

Commented by MJS last updated on 02/Mar/20

P= ((x),(y) ) = ((x),((6−x^2 )) ); distance^2 is x^2 +(3−x^2 )^2 =x^4 −5x^2 +9; (d/dx)[x^4 −5x^2 +9]=0 ⇔ x(x^2 −(5/2))=0 ⇒ x=0∨x=±((√(10))/2) ⇒ min at x=±((√(10))/2) ⇒ min dist. = ((√(11))/2)

$${P}=\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\begin{pmatrix}{{x}}\\{\mathrm{6}−{x}^{\mathrm{2}} }\end{pmatrix};\:\mathrm{distance}^{\mathrm{2}} \:\mathrm{is}\:{x}^{\mathrm{2}} +\left(\mathrm{3}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} ={x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{9};\:\frac{{d}}{{dx}}\left[{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{9}\right]=\mathrm{0}\:\Leftrightarrow\:{x}\left({x}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{2}}\right)=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{0}\vee{x}=\pm\frac{\sqrt{\mathrm{10}}}{\mathrm{2}}\:\Rightarrow\:\mathrm{min}\:\mathrm{at}\:{x}=\pm\frac{\sqrt{\mathrm{10}}}{\mathrm{2}}\:\Rightarrow\:\mathrm{min}\:\mathrm{dist}.\:=\:\frac{\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$

Answered by john santu last updated on 02/Mar/20

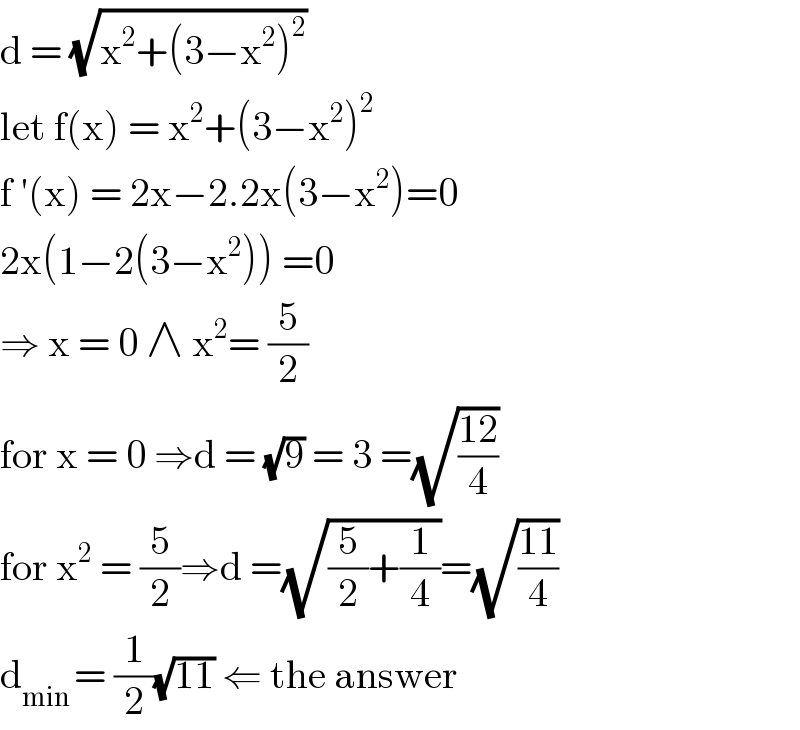
d = (√(x^2 +(3−x^2 )^2 )) let f(x) = x^2 +(3−x^2 )^2 f ′(x) = 2x−2.2x(3−x^2 )=0 2x(1−2(3−x^2 )) =0 ⇒ x = 0 ∧ x^2 = (5/2) for x = 0 ⇒d = (√9) = 3 =(√((12)/4)) for x^2 = (5/2)⇒d =(√((5/2)+(1/4)))=(√((11)/4)) d_(min ) = (1/2)(√(11)) ⇐ the answer

$$\mathrm{d}\:=\:\sqrt{\mathrm{x}^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x}^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)\:=\:\mathrm{2x}−\mathrm{2}.\mathrm{2x}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{2x}\left(\mathrm{1}−\mathrm{2}\left(\mathrm{3}−\mathrm{x}^{\mathrm{2}} \right)\right)\:=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}\:=\:\mathrm{0}\:\wedge\:\mathrm{x}^{\mathrm{2}} =\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{x}\:=\:\mathrm{0}\:\Rightarrow\mathrm{d}\:=\:\sqrt{\mathrm{9}}\:=\:\mathrm{3}\:=\sqrt{\frac{\mathrm{12}}{\mathrm{4}}} \\ $$$$\mathrm{for}\:\mathrm{x}^{\mathrm{2}} \:=\:\frac{\mathrm{5}}{\mathrm{2}}\Rightarrow\mathrm{d}\:=\sqrt{\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}}=\sqrt{\frac{\mathrm{11}}{\mathrm{4}}} \\ $$$$\mathrm{d}_{\mathrm{min}\:} =\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{11}}\:\Leftarrow\:\mathrm{the}\:\mathrm{answer} \\ $$

Answered by mr W last updated on 02/Mar/20

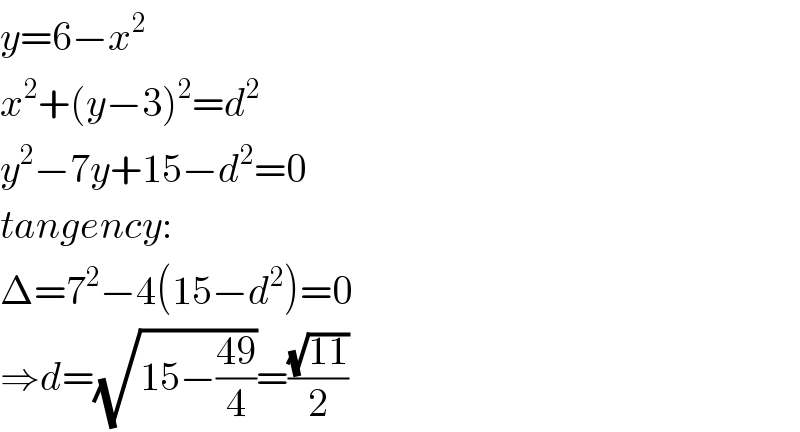
y=6−x^2 x^2 +(y−3)^2 =d^2 y^2 −7y+15−d^2 =0 tangency: Δ=7^2 −4(15−d^2 )=0 ⇒d=(√(15−((49)/4)))=((√(11))/2)

$${y}=\mathrm{6}−{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} ={d}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −\mathrm{7}{y}+\mathrm{15}−{d}^{\mathrm{2}} =\mathrm{0} \\ $$$${tangency}: \\ $$$$\Delta=\mathrm{7}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{15}−{d}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{d}=\sqrt{\mathrm{15}−\frac{\mathrm{49}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$

Commented by john santu last updated on 03/Mar/20

what is tangency sir?

$$\mathrm{what}\:\mathrm{is}\:\mathrm{tangency}\:\mathrm{sir}? \\ $$

Commented by mr W last updated on 03/Mar/20

if the circle x^2 +(y−3)^2 =d^2 tangents the parabola y=6−x^2 , then radius d of the circle is the smallest distance from the point (0,3) to curve y=6−x^2 . when both curves tangent each other, the equation y^2 −7y+15−d^2 =0 has one and only one solution, this is what “tangency”means.

$${if}\:{the}\:{circle}\:{x}^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} ={d}^{\mathrm{2}} \:{tangents} \\ $$$${the}\:{parabola}\:{y}=\mathrm{6}−{x}^{\mathrm{2}} ,\:{then}\:{radius}\:{d} \\ $$$${of}\:{the}\:{circle}\:{is}\:{the}\:{smallest}\:{distance} \\ $$$${from}\:{the}\:{point}\:\left(\mathrm{0},\mathrm{3}\right)\:{to}\:{curve}\:{y}=\mathrm{6}−{x}^{\mathrm{2}} . \\ $$$${when}\:{both}\:{curves}\:{tangent}\:{each}\:{other}, \\ $$$${the}\:{equation}\:{y}^{\mathrm{2}} −\mathrm{7}{y}+\mathrm{15}−{d}^{\mathrm{2}} =\mathrm{0}\:{has} \\ $$$${one}\:{and}\:{only}\:{one}\:{solution},\:{this}\:{is} \\ $$$${what}\:``{tangency}''{means}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com