Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 83639 by niroj last updated on 04/Mar/20

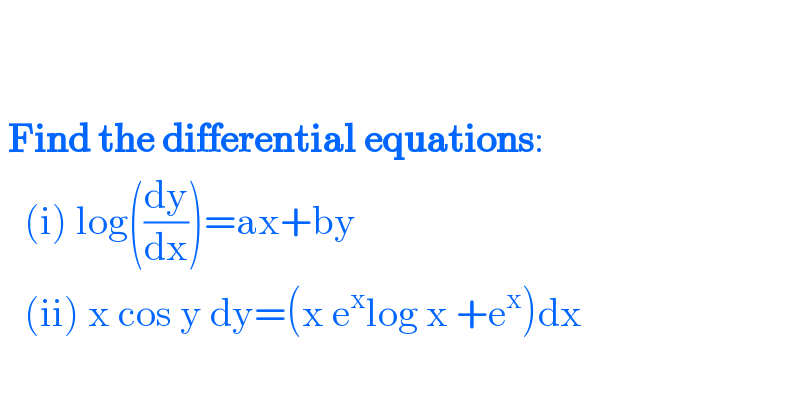
Find the differential equations: (i) log((dy/dx))=ax+by (ii) x cos y dy=(x e^x log x +e^x )dx

$$ \\ $$$$\: \\ $$$$\:\boldsymbol{\mathrm{Find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{differential}}\:\boldsymbol{\mathrm{equations}}: \\ $$$$\:\:\:\left(\mathrm{i}\right)\:\mathrm{log}\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)=\mathrm{ax}+\mathrm{by} \\ $$$$\:\:\:\left(\mathrm{ii}\right)\:\mathrm{x}\:\mathrm{cos}\:\mathrm{y}\:\mathrm{dy}=\left(\mathrm{x}\:\mathrm{e}^{\mathrm{x}} \mathrm{log}\:\mathrm{x}\:+\mathrm{e}^{\mathrm{x}} \right)\mathrm{dx} \\ $$$$ \\ $$

Answered by TANMAY PANACEA last updated on 05/Mar/20

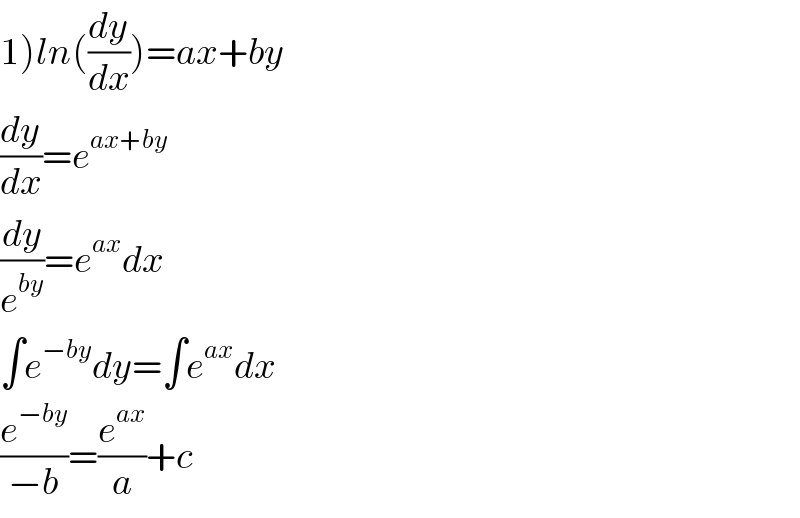
1)ln((dy/dx))=ax+by (dy/dx)=e^(ax+by) (dy/e^(by) )=e^(ax) dx ∫e^(−by) dy=∫e^(ax) dx (e^(−by) /(−b))=(e^(ax) /a)+c

$$\left.\mathrm{1}\right){ln}\left(\frac{{dy}}{{dx}}\right)={ax}+{by} \\ $$$$\frac{{dy}}{{dx}}={e}^{{ax}+{by}} \\ $$$$\frac{{dy}}{{e}^{{by}} }={e}^{{ax}} {dx} \\ $$$$\int{e}^{−{by}} {dy}=\int{e}^{{ax}} {dx} \\ $$$$\frac{{e}^{−{by}} }{−{b}}=\frac{{e}^{{ax}} }{{a}}+{c} \\ $$

Commented by niroj last updated on 05/Mar/20

its ★ great

$${its}\:\bigstar\:{great} \\ $$

Commented by TANMAY PANACEA last updated on 05/Mar/20

most welcome

$${most}\:{welcome}\: \\ $$

Answered by TANMAY PANACEA last updated on 05/Mar/20

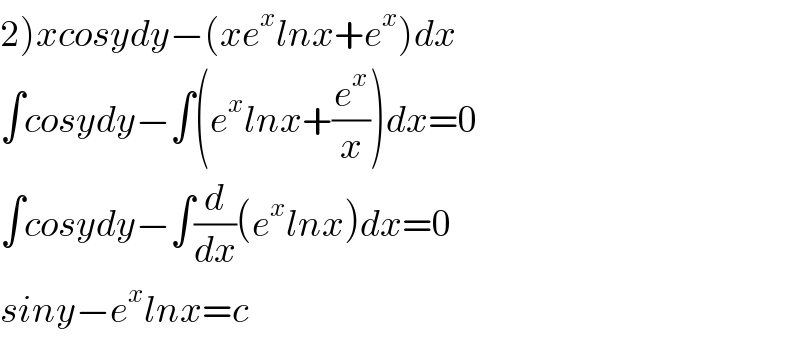
2)xcosydy−(xe^x lnx+e^x )dx ∫cosydy−∫(e^x lnx+(e^x /x))dx=0 ∫cosydy−∫(d/dx)(e^x lnx)dx=0 siny−e^x lnx=c

$$\left.\mathrm{2}\right){xcosydy}−\left({xe}^{{x}} {lnx}+{e}^{{x}} \right){dx} \\ $$$$\int{cosydy}−\int\left({e}^{{x}} {lnx}+\frac{{e}^{{x}} }{{x}}\right){dx}=\mathrm{0} \\ $$$$\int{cosydy}−\int\frac{{d}}{{dx}}\left({e}^{{x}} {lnx}\right){dx}=\mathrm{0} \\ $$$${siny}−{e}^{{x}} {lnx}={c} \\ $$

Commented by niroj last updated on 05/Mar/20

thank you panacea.

$$\:{thank}\:{you}\:{panacea}. \\ $$

Commented by TANMAY PANACEA last updated on 05/Mar/20

most welcome

$${most}\:{welcome} \\ $$

Answered by M±th+et£s last updated on 05/Mar/20

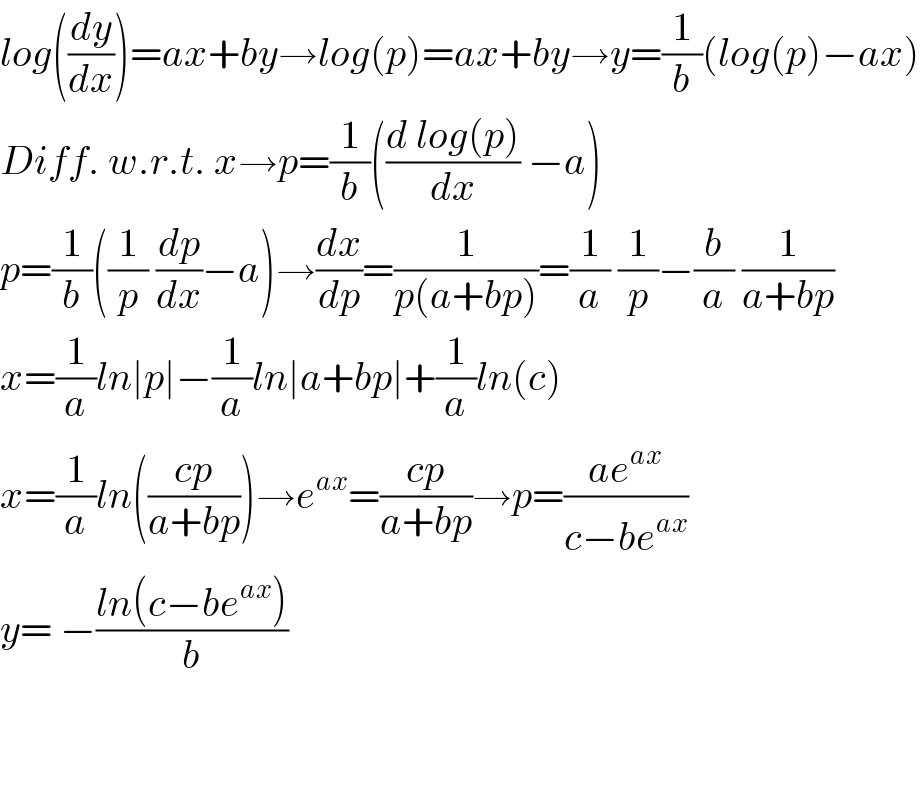
log((dy/dx))=ax+by→log(p)=ax+by→y=(1/b)(log(p)−ax) Diff. w.r.t. x→p=(1/b)(((d log(p))/dx) −a) p=(1/b)((1/p) (dp/dx)−a)→(dx/dp)=(1/(p(a+bp)))=(1/a) (1/p)−(b/a) (1/(a+bp)) x=(1/a)ln∣p∣−(1/a)ln∣a+bp∣+(1/a)ln(c) x=(1/a)ln(((cp)/(a+bp)))→e^(ax) =((cp)/(a+bp))→p=((ae^(ax) )/(c−be^(ax) )) y= −((ln(c−be^(ax) ))/b)

$${log}\left(\frac{{dy}}{{dx}}\right)={ax}+{by}\rightarrow{log}\left({p}\right)={ax}+{by}\rightarrow{y}=\frac{\mathrm{1}}{{b}}\left({log}\left({p}\right)−{ax}\right) \\ $$$${Diff}.\:{w}.{r}.{t}.\:{x}\rightarrow{p}=\frac{\mathrm{1}}{{b}}\left(\frac{{d}\:{log}\left({p}\right)}{{dx}}\:−{a}\right) \\ $$$${p}=\frac{\mathrm{1}}{{b}}\left(\frac{\mathrm{1}}{{p}}\:\frac{{dp}}{{dx}}−{a}\right)\rightarrow\frac{{dx}}{{dp}}=\frac{\mathrm{1}}{{p}\left({a}+{bp}\right)}=\frac{\mathrm{1}}{{a}}\:\frac{\mathrm{1}}{{p}}−\frac{{b}}{{a}}\:\frac{\mathrm{1}}{{a}+{bp}} \\ $$$${x}=\frac{\mathrm{1}}{{a}}{ln}\mid{p}\mid−\frac{\mathrm{1}}{{a}}{ln}\mid{a}+{bp}\mid+\frac{\mathrm{1}}{{a}}{ln}\left({c}\right) \\ $$$${x}=\frac{\mathrm{1}}{{a}}{ln}\left(\frac{{cp}}{{a}+{bp}}\right)\rightarrow{e}^{{ax}} =\frac{{cp}}{{a}+{bp}}\rightarrow{p}=\frac{{ae}^{{ax}} }{{c}−{be}^{{ax}} } \\ $$$${y}=\:−\frac{{ln}\left({c}−{be}^{{ax}} \right)}{{b}} \\ $$$$ \\ $$$$ \\ $$

Answered by M±th+et£s last updated on 05/Mar/20

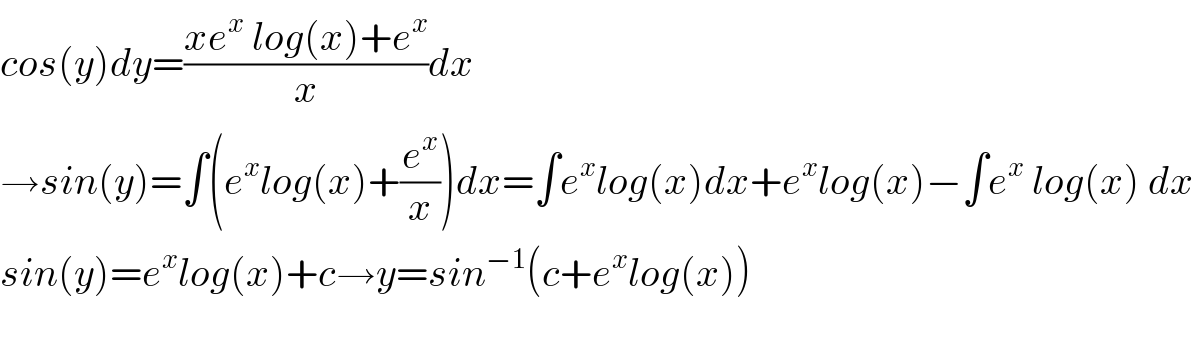
cos(y)dy=((xe^x log(x)+e^x )/x)dx →sin(y)=∫(e^x log(x)+(e^x /x))dx=∫e^x log(x)dx+e^x log(x)−∫e^x log(x) dx sin(y)=e^x log(x)+c→y=sin^(−1) (c+e^x log(x))

$${cos}\left({y}\right){dy}=\frac{{xe}^{{x}} \:{log}\left({x}\right)+{e}^{{x}} }{{x}}{dx} \\ $$$$\rightarrow{sin}\left({y}\right)=\int\left({e}^{{x}} {log}\left({x}\right)+\frac{{e}^{{x}} }{{x}}\right){dx}=\int{e}^{{x}} {log}\left({x}\right){dx}+{e}^{{x}} {log}\left({x}\right)−\int{e}^{{x}} \:{log}\left({x}\right)\:{dx} \\ $$$${sin}\left({y}\right)={e}^{{x}} {log}\left({x}\right)+{c}\rightarrow{y}={sin}^{−\mathrm{1}} \left({c}+{e}^{{x}} {log}\left({x}\right)\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com