Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 83898 by sahnaz last updated on 07/Mar/20

∫(du/((√(u^2 −1 ))−u))

$$\int\frac{\mathrm{du}}{\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}\:}−\mathrm{u}} \\ $$

Commented by john santu last updated on 07/Mar/20

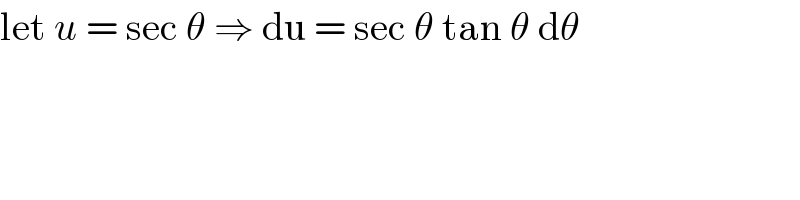
let u = sec θ ⇒ du = sec θ tan θ dθ

$$\mathrm{let}\:{u}\:=\:\mathrm{sec}\:\theta\:\Rightarrow\:\mathrm{du}\:=\:\mathrm{sec}\:\theta\:\mathrm{tan}\:\theta\:\mathrm{d}\theta \\ $$

Commented by john santu last updated on 07/Mar/20

∫ ((sec θ tan θ)/(tan θ − sec θ)) dθ = ∫ ((sec θ tan θ (tan θ+sec θ))/(−1)) dθ −[∫sec θ tan^2 θ + tan θ sec^2 θ dθ] =−∫ sec θ (sec^2 θ−1)dθ−(1/2)tan^2 θ = −∫sec θ d(tan θ)+ln ∣sec θ+tan θ∣−(1/2)tan^2 θ

$$\int\:\frac{\mathrm{sec}\:\theta\:\mathrm{tan}\:\theta}{\mathrm{tan}\:\theta\:−\:\mathrm{sec}\:\theta}\:\mathrm{d}\theta\:=\: \\ $$$$\int\:\frac{\mathrm{sec}\:\theta\:\mathrm{tan}\:\theta\:\left(\mathrm{tan}\:\theta+\mathrm{sec}\:\theta\right)}{−\mathrm{1}}\:\mathrm{d}\theta \\ $$$$−\left[\int\mathrm{sec}\:\theta\:\mathrm{tan}\:^{\mathrm{2}} \theta\:+\:\mathrm{tan}\:\theta\:\mathrm{sec}\:^{\mathrm{2}} \theta\:\mathrm{d}\theta\right] \\ $$$$=−\int\:\mathrm{sec}\:\theta\:\left(\mathrm{sec}\:^{\mathrm{2}} \theta−\mathrm{1}\right)\mathrm{d}\theta−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:^{\mathrm{2}} \theta\: \\ $$$$=\:−\int\mathrm{sec}\:\theta\:\mathrm{d}\left(\mathrm{tan}\:\theta\right)+\mathrm{ln}\:\mid\mathrm{sec}\:\theta+\mathrm{tan}\:\theta\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:^{\mathrm{2}} \theta \\ $$$$ \\ $$

Commented by john santu last updated on 07/Mar/20

it easy to solving

$$\mathrm{it}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solving} \\ $$

Commented by mathmax by abdo last updated on 07/Mar/20

I=∫ (du/((√(u^2 −1))−u)) we use the changement u=ch(t) ⇒ I =∫ ((sh(t)dt)/(sh(t)−ch(t))) =∫ (((e^t −e^(−t) )/2)/(((e^t −e^(−t) )/2)−((e^t +e^(−t) )/2)))dt =∫ ((e^t −e^(−t) )/(e^t −e^(−t) −e^t −e^(−t) )) dt =∫ ((e^t −e^(−t) )/(−2e^(−t) ))dt =∫((e^(2t) −1)/(−2))dt =−(1/2)∫ (e^(2t) −1)dt =−(1/4)e^(2t) +(t/2) +C t=argch(u) =ln(u+(√(u^2 −1))) ⇒e^(2t) =(u+(√(u^2 −1)))^2 ⇒ I =−(1/4)(u+(√(u^2 −1)))^2 +(1/2)ln(u+(√(u^2 −1)))+C

$${I}=\int\:\frac{{du}}{\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}−{u}}\:\:\:{we}\:{use}\:{the}\:{changement}\:{u}={ch}\left({t}\right)\:\Rightarrow \\ $$$${I}\:=\int\:\:\frac{{sh}\left({t}\right){dt}}{{sh}\left({t}\right)−{ch}\left({t}\right)}\:=\int\:\frac{\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}}{\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}−\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}}{dt} \\ $$$$=\int\:\:\:\frac{{e}^{{t}} −{e}^{−{t}} }{{e}^{{t}} −{e}^{−{t}} −{e}^{{t}} −{e}^{−{t}} }\:{dt}\:=\int\:\:\frac{{e}^{{t}} \:−{e}^{−{t}} }{−\mathrm{2}{e}^{−{t}} }{dt}\:\:=\int\frac{{e}^{\mathrm{2}{t}} −\mathrm{1}}{−\mathrm{2}}{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\left({e}^{\mathrm{2}{t}} −\mathrm{1}\right){dt}\:=−\frac{\mathrm{1}}{\mathrm{4}}{e}^{\mathrm{2}{t}} \:+\frac{{t}}{\mathrm{2}}\:+{C} \\ $$$${t}={argch}\left({u}\right)\:={ln}\left({u}+\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}\right)\:\Rightarrow{e}^{\mathrm{2}{t}} \:=\left({u}+\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{4}}\left({u}+\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({u}+\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com