Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 85131 by Rio Michael last updated on 19/Mar/20

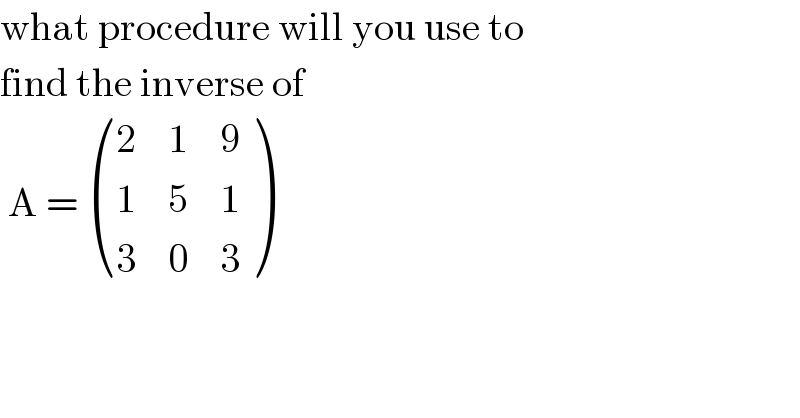
what procedure will you use to find the inverse of A = ((2,1,9),(1,5,1),(3,0,3) )

$$\mathrm{what}\:\mathrm{procedure}\:\mathrm{will}\:\mathrm{you}\:\mathrm{use}\:\mathrm{to}\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{inverse}\:\mathrm{of} \\ $$$$\:\mathrm{A}\:=\:\begin{pmatrix}{\mathrm{2}}&{\mathrm{1}}&{\mathrm{9}}\\{\mathrm{1}}&{\mathrm{5}}&{\mathrm{1}}\\{\mathrm{3}}&{\mathrm{0}}&{\mathrm{3}}\end{pmatrix} \\ $$

Commented by jagoll last updated on 19/Mar/20

(1) find ∣A∣ (2) find adj (A) (3) if ∣A∣ ≠ 0 then A^(−1) = (1/(∣A∣)) ×adj(A)

$$\left(\mathrm{1}\right)\:\mathrm{find}\:\mid\mathrm{A}\mid\: \\ $$$$\left(\mathrm{2}\right)\:\mathrm{find}\:\mathrm{adj}\:\left(\mathrm{A}\right) \\ $$$$\left(\mathrm{3}\right)\:\mathrm{if}\:\mid\mathrm{A}\mid\:\neq\:\mathrm{0}\:\mathrm{then} \\ $$$$\mathrm{A}^{−\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mid\mathrm{A}\mid}\:×\mathrm{adj}\left(\mathrm{A}\right) \\ $$

Commented by Rio Michael last updated on 19/Mar/20

thanks

$$\mathrm{thanks} \\ $$

Commented by mathmax by abdo last updated on 19/Mar/20

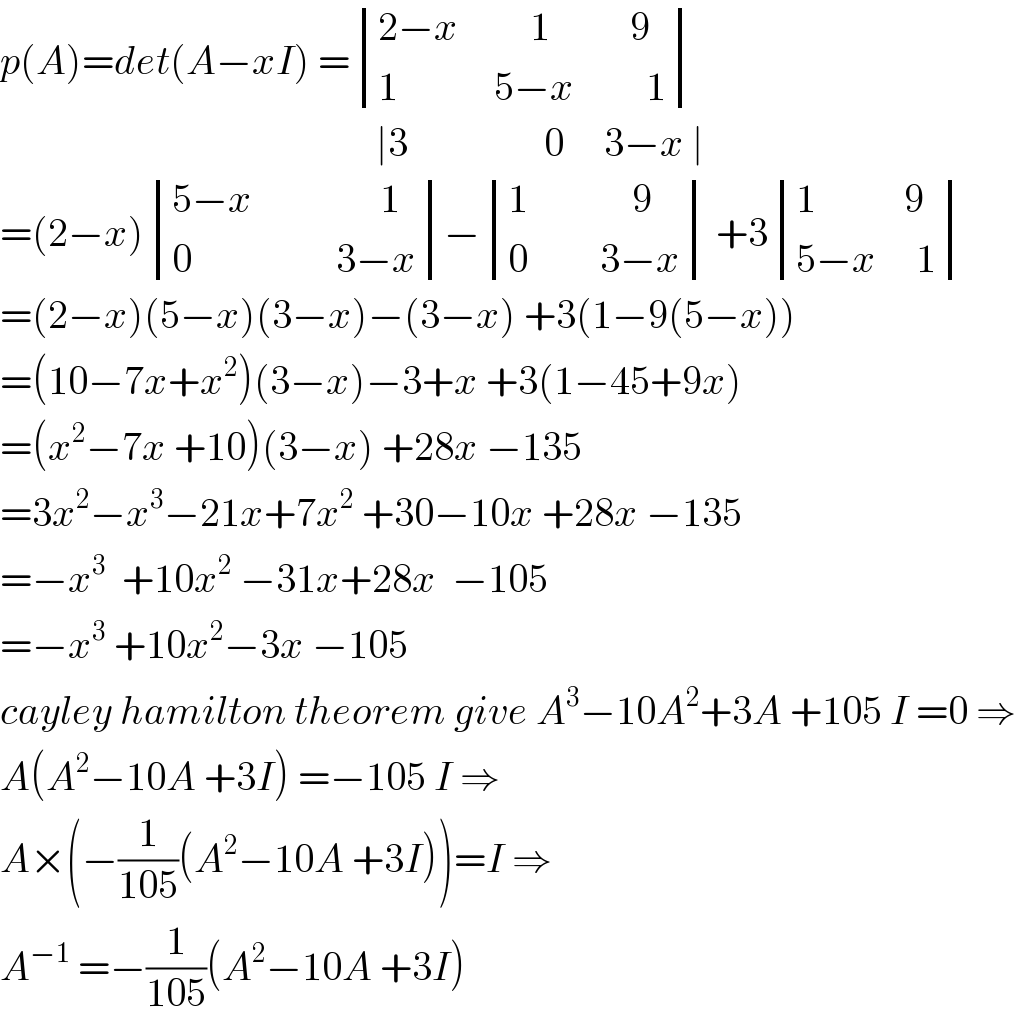
p(A)=det(A−xI) = determinant (((2−x 1 9)),((1 5−x 1))) ∣3 0 3−x ∣ =(2−x) determinant (((5−x 1)),((0 3−x)))− determinant (((1 9)),((0 3−x))) +3 determinant (((1 9)),((5−x 1))) =(2−x)(5−x)(3−x)−(3−x) +3(1−9(5−x)) =(10−7x+x^2 )(3−x)−3+x +3(1−45+9x) =(x^2 −7x +10)(3−x) +28x −135 =3x^2 −x^3 −21x+7x^2 +30−10x +28x −135 =−x^3 +10x^2 −31x+28x −105 =−x^3 +10x^2 −3x −105 cayley hamilton theorem give A^3 −10A^2 +3A +105 I =0 ⇒ A(A^2 −10A +3I) =−105 I ⇒ A×(−(1/(105))(A^2 −10A +3I))=I ⇒ A^(−1) =−(1/(105))(A^2 −10A +3I)

$${p}\left({A}\right)={det}\left({A}−{xI}\right)\:=\begin{vmatrix}{\mathrm{2}−{x}\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{9}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}−{x}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\mathrm{3}−{x}\:\mid \\ $$$$=\left(\mathrm{2}−{x}\right)\begin{vmatrix}{\mathrm{5}−{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}−{x}}\end{vmatrix}−\begin{vmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{3}−{x}}\end{vmatrix}\:+\mathrm{3}\begin{vmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}}\\{\mathrm{5}−{x}\:\:\:\:\:\mathrm{1}}\end{vmatrix} \\ $$$$=\left(\mathrm{2}−{x}\right)\left(\mathrm{5}−{x}\right)\left(\mathrm{3}−{x}\right)−\left(\mathrm{3}−{x}\right)\:+\mathrm{3}\left(\mathrm{1}−\mathrm{9}\left(\mathrm{5}−{x}\right)\right) \\ $$$$=\left(\mathrm{10}−\mathrm{7}{x}+{x}^{\mathrm{2}} \right)\left(\mathrm{3}−{x}\right)−\mathrm{3}+{x}\:+\mathrm{3}\left(\mathrm{1}−\mathrm{45}+\mathrm{9}{x}\right) \\ $$$$=\left({x}^{\mathrm{2}} −\mathrm{7}{x}\:+\mathrm{10}\right)\left(\mathrm{3}−{x}\right)\:+\mathrm{28}{x}\:−\mathrm{135} \\ $$$$=\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{3}} −\mathrm{21}{x}+\mathrm{7}{x}^{\mathrm{2}} \:+\mathrm{30}−\mathrm{10}{x}\:+\mathrm{28}{x}\:−\mathrm{135} \\ $$$$=−{x}^{\mathrm{3}} \:\:+\mathrm{10}{x}^{\mathrm{2}} \:−\mathrm{31}{x}+\mathrm{28}{x}\:\:−\mathrm{105} \\ $$$$=−{x}^{\mathrm{3}} \:+\mathrm{10}{x}^{\mathrm{2}} −\mathrm{3}{x}\:−\mathrm{105} \\ $$$${cayley}\:{hamilton}\:{theorem}\:{give}\:{A}^{\mathrm{3}} −\mathrm{10}{A}^{\mathrm{2}} +\mathrm{3}{A}\:+\mathrm{105}\:{I}\:=\mathrm{0}\:\Rightarrow \\ $$$${A}\left({A}^{\mathrm{2}} −\mathrm{10}{A}\:+\mathrm{3}{I}\right)\:=−\mathrm{105}\:{I}\:\Rightarrow \\ $$$${A}×\left(−\frac{\mathrm{1}}{\mathrm{105}}\left({A}^{\mathrm{2}} −\mathrm{10}{A}\:+\mathrm{3}{I}\right)\right)={I}\:\Rightarrow \\ $$$${A}^{−\mathrm{1}} \:=−\frac{\mathrm{1}}{\mathrm{105}}\left({A}^{\mathrm{2}} −\mathrm{10}{A}\:+\mathrm{3}{I}\right) \\ $$

Commented by mathmax by abdo last updated on 19/Mar/20

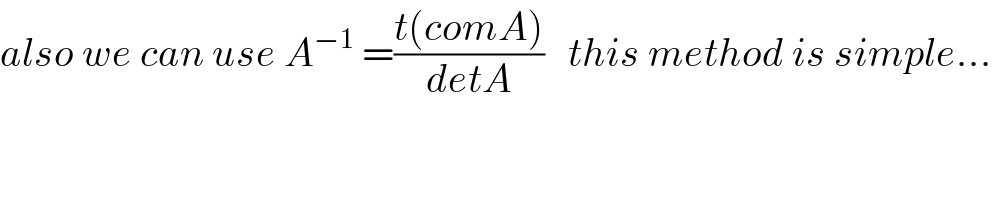
also we can use A^(−1) =((t(comA))/(detA)) this method is simple...

$${also}\:{we}\:{can}\:{use}\:{A}^{−\mathrm{1}} \:=\frac{{t}\left({comA}\right)}{{detA}}\:\:\:{this}\:{method}\:{is}\:{simple}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com