Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 85160 by mathmax by abdo last updated on 19/Mar/20

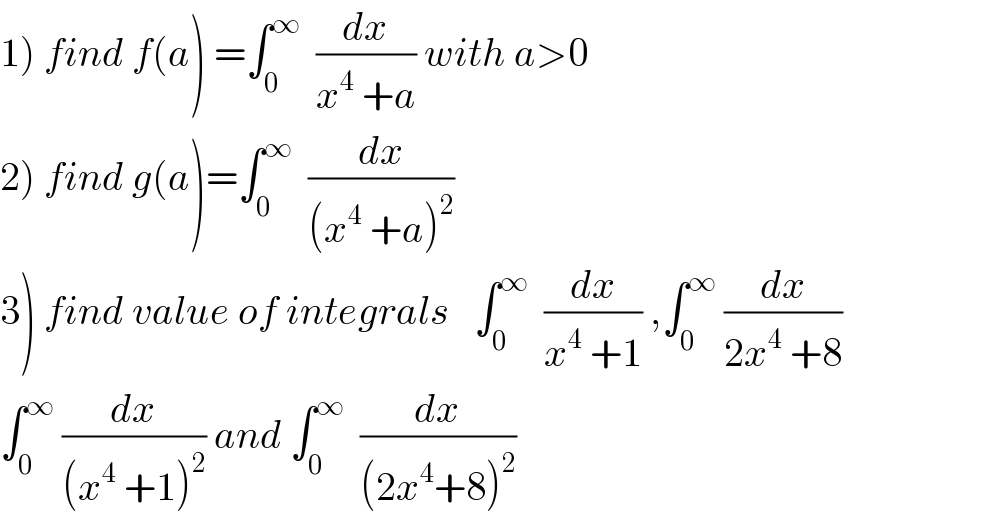
1) find f(a) =∫_0 ^∞ (dx/(x^4 +a)) with a>0 2) find g(a)=∫_0 ^∞ (dx/((x^4 +a)^2 )) 3) find value of integrals ∫_0 ^∞ (dx/(x^4 +1)) ,∫_0 ^∞ (dx/(2x^4 +8)) ∫_0 ^∞ (dx/((x^4 +1)^2 )) and ∫_0 ^∞ (dx/((2x^4 +8)^2 ))

$$\left.\mathrm{1}\right)\:{find}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+{a}}\:{with}\:{a}>\mathrm{0} \\ $$ $$\left.\mathrm{2}\right)\:{find}\:{g}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+{a}\right)^{\mathrm{2}} } \\ $$ $$\left.\mathrm{3}\right)\:{find}\:{value}\:{of}\:{integrals}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+\mathrm{1}}\:,\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\mathrm{2}{x}^{\mathrm{4}} \:+\mathrm{8}} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{and}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left(\mathrm{2}{x}^{\mathrm{4}} +\mathrm{8}\right)^{\mathrm{2}} } \\ $$

Commented bymathmax by abdo last updated on 19/Mar/20

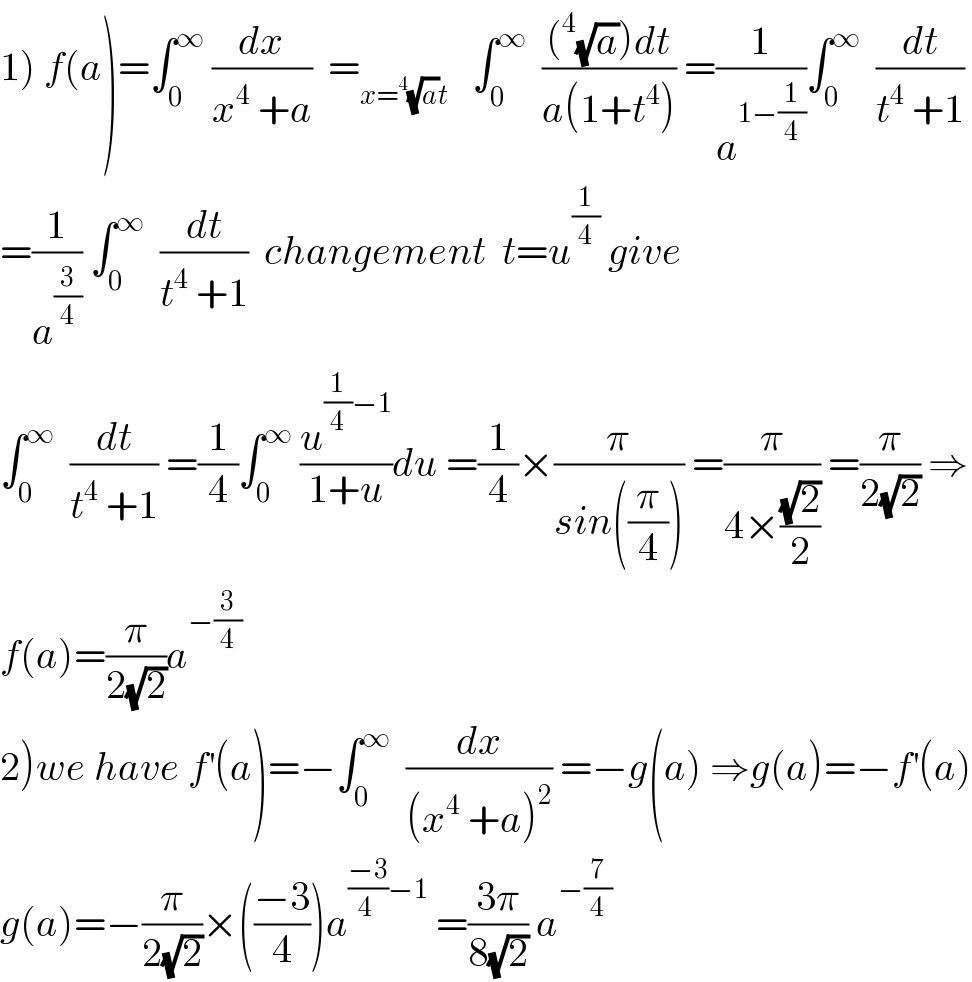
1) f(a)=∫_0 ^∞ (dx/(x^4 +a)) =_(x=^4 (√a)t) ∫_0 ^∞ (((^4 (√a))dt)/(a(1+t^4 ))) =(1/a^(1−(1/4)) )∫_0 ^∞ (dt/(t^4 +1)) =(1/a^(3/4) ) ∫_0 ^∞ (dt/(t^4 +1)) changement t=u^(1/4) give ∫_0 ^∞ (dt/(t^4 +1)) =(1/4)∫_0 ^∞ (u^((1/4)−1) /(1+u))du =(1/4)×(π/(sin((π/4)))) =(π/(4×((√2)/2))) =(π/(2(√2))) ⇒ f(a)=(π/(2(√2)))a^(−(3/4)) 2)we have f^′ (a)=−∫_0 ^∞ (dx/((x^4 +a)^2 )) =−g(a) ⇒g(a)=−f^′ (a) g(a)=−(π/(2(√2)))×(((−3)/4))a^(((−3)/(4 ))−1) =((3π)/(8(√2))) a^(−(7/4))

$$\left.\mathrm{1}\right)\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{{x}^{\mathrm{4}} \:+{a}}\:\:=_{{x}=^{\mathrm{4}} \sqrt{{a}}{t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left(^{\mathrm{4}} \sqrt{{a}}\right){dt}}{{a}\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}\:=\frac{\mathrm{1}}{{a}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}} }\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{4}} \:+\mathrm{1}} \\ $$ $$=\frac{\mathrm{1}}{{a}^{\frac{\mathrm{3}}{\mathrm{4}}} }\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:\:{changement}\:\:{t}={u}^{\frac{\mathrm{1}}{\mathrm{4}}} \:{give} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{u}}{du}\:=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\mathrm{4}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$ $${f}\left({a}\right)=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}{a}^{−\frac{\mathrm{3}}{\mathrm{4}}} \\ $$ $$\left.\mathrm{2}\right){we}\:{have}\:{f}^{'} \left({a}\right)=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+{a}\right)^{\mathrm{2}} }\:=−{g}\left({a}\right)\:\Rightarrow{g}\left({a}\right)=−{f}^{'} \left({a}\right) \\ $$ $${g}\left({a}\right)=−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}×\left(\frac{−\mathrm{3}}{\mathrm{4}}\right){a}^{\frac{−\mathrm{3}}{\mathrm{4}\:}−\mathrm{1}} \:=\frac{\mathrm{3}\pi}{\mathrm{8}\sqrt{\mathrm{2}}}\:{a}^{−\frac{\mathrm{7}}{\mathrm{4}}} \\ $$

Commented bymathmax by abdo last updated on 19/Mar/20

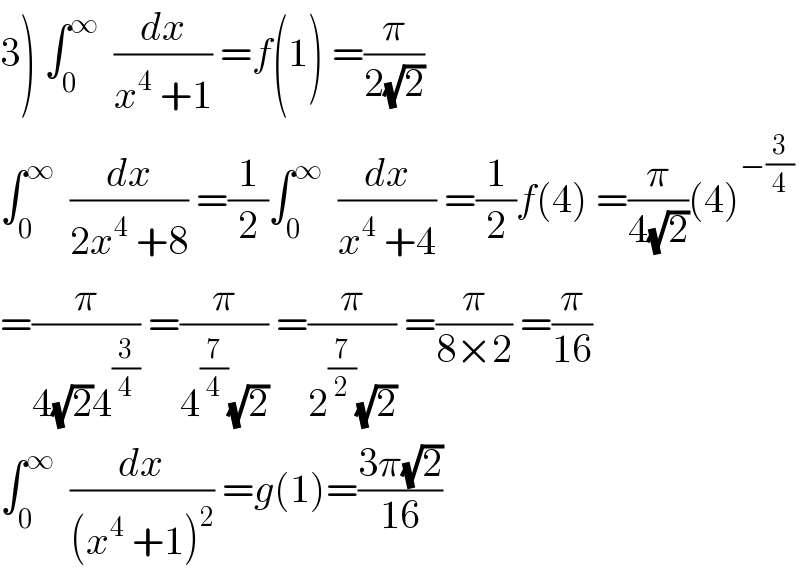
3) ∫_0 ^∞ (dx/(x^4 +1)) =f(1) =(π/(2(√2))) ∫_0 ^∞ (dx/(2x^4 +8)) =(1/2)∫_0 ^∞ (dx/(x^4 +4)) =(1/2)f(4) =(π/(4(√2)))(4)^(−(3/4)) =(π/(4(√2)4^(3/4) )) =(π/(4^(7/4) (√2))) =(π/(2^(7/2) (√2))) =(π/(8×2)) =(π/(16)) ∫_0 ^∞ (dx/((x^4 +1)^2 )) =g(1)=((3π(√2))/(16))

$$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+\mathrm{1}}\:={f}\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{2}{x}^{\mathrm{4}} \:+\mathrm{8}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{2}}{f}\left(\mathrm{4}\right)\:=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\left(\mathrm{4}\right)^{−\frac{\mathrm{3}}{\mathrm{4}}} \\ $$ $$=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{4}}} }\:=\frac{\pi}{\mathrm{4}^{\frac{\mathrm{7}}{\mathrm{4}}} \sqrt{\mathrm{2}}}\:=\frac{\pi}{\mathrm{2}^{\frac{\mathrm{7}}{\mathrm{2}}} \sqrt{\mathrm{2}}}\:=\frac{\pi}{\mathrm{8}×\mathrm{2}}\:=\frac{\pi}{\mathrm{16}} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:={g}\left(\mathrm{1}\right)=\frac{\mathrm{3}\pi\sqrt{\mathrm{2}}}{\mathrm{16}} \\ $$

Answered by mind is power last updated on 19/Mar/20

x=(√((√a)tg(t)))⇒ f(a)=∫_0 ^(π/2) (((√(√a))(1+tg^2 (t)))/(2(√(tg(t))))).(dt/(a(1+tg^2 (t)))) =(1/(2a^(3/4) )).∫_0 ^(π/2) cos^(1/2) (t)sin^((−1)/2) (t)dt =(1/(2a^(3/4) )).((β((3/4),(1/4)))/2)=(1/(4a^(3/4) )).((Γ((1/4))Γ((3/4)))/(Γ(1)))=(π/(4a^(3/4) sin((π/4)))) =((π(√2))/(4a^(3/4) ))=f(a) g(a)=−f′(a)=((3π(√2))/(16a^(7/4) )). ∫_0 ^(+∞) (dx/(x^4 +1))=f(1)=((π(√2))/4)=(π/(2(√2))) ∫_0 ^(+∞) (dx/(2x^4 +8))=((f(4))/2)=((π(√2))/(8(2^(3/2) )))=(π/(16)) ∫(dx/((1+x^4 )^2 ))=g(1)=−f′(1)=((3π(√2))/(16)) ∫_0 ^(+∞) (dx/((2x^4 +8)^2 ))=(1/4)g(4)=−((f′(4))/4)=((3π(√2))/(64.4^(7/4) )) =((3π)/(512))

$${x}=\sqrt{\sqrt{{a}}{tg}\left({t}\right)}\Rightarrow \\ $$ $${f}\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\sqrt{\sqrt{{a}}}\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right)}{\mathrm{2}\sqrt{{tg}\left({t}\right)}}.\frac{{dt}}{{a}\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right)} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}{a}^{\frac{\mathrm{3}}{\mathrm{4}}} }.\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({t}\right){sin}^{\frac{−\mathrm{1}}{\mathrm{2}}} \left({t}\right){dt} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}{a}^{\frac{\mathrm{3}}{\mathrm{4}}} }.\frac{\beta\left(\frac{\mathrm{3}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}{a}^{\frac{\mathrm{3}}{\mathrm{4}}} }.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\Gamma\left(\mathrm{1}\right)}=\frac{\pi}{\mathrm{4}{a}^{\frac{\mathrm{3}}{\mathrm{4}}} {sin}\left(\frac{\pi}{\mathrm{4}}\right)} \\ $$ $$=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}{a}^{\frac{\mathrm{3}}{\mathrm{4}}} }={f}\left({a}\right) \\ $$ $${g}\left({a}\right)=−{f}'\left({a}\right)=\frac{\mathrm{3}\pi\sqrt{\mathrm{2}}}{\mathrm{16}{a}^{\frac{\mathrm{7}}{\mathrm{4}}} }. \\ $$ $$\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{{x}^{\mathrm{4}} +\mathrm{1}}={f}\left(\mathrm{1}\right)=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$ $$\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{\mathrm{2}{x}^{\mathrm{4}} +\mathrm{8}}=\frac{{f}\left(\mathrm{4}\right)}{\mathrm{2}}=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}\left(\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)}=\frac{\pi}{\mathrm{16}} \\ $$ $$\int\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{4}} \right)^{\mathrm{2}} }={g}\left(\mathrm{1}\right)=−{f}'\left(\mathrm{1}\right)=\frac{\mathrm{3}\pi\sqrt{\mathrm{2}}}{\mathrm{16}} \\ $$ $$\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{\left(\mathrm{2}{x}^{\mathrm{4}} +\mathrm{8}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}{g}\left(\mathrm{4}\right)=−\frac{{f}'\left(\mathrm{4}\right)}{\mathrm{4}}=\frac{\mathrm{3}\pi\sqrt{\mathrm{2}}}{\mathrm{64}.\mathrm{4}^{\frac{\mathrm{7}}{\mathrm{4}}} } \\ $$ $$=\frac{\mathrm{3}\pi}{\mathrm{512}} \\ $$ $$ \\ $$

Commented bymathmax by abdo last updated on 19/Mar/20

thank you sir.

$${thank}\:{you}\:{sir}. \\ $$

Commented bymind is power last updated on 19/Mar/20

withe pleasur

$${withe}\:{pleasur} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com