Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 85260 by Umar last updated on 20/Mar/20

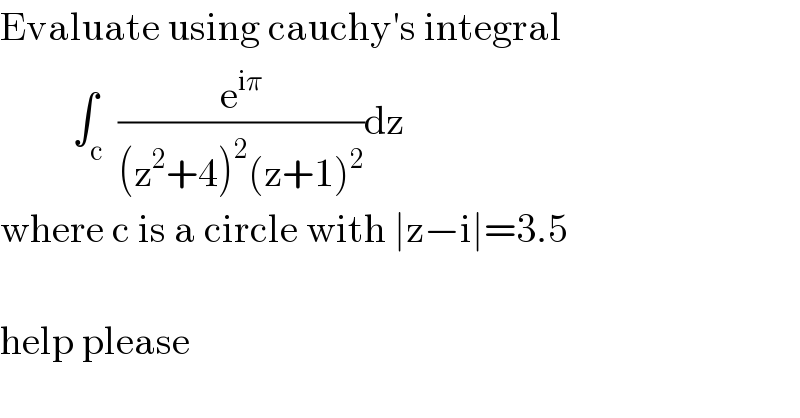
Evaluate using cauchy′s integral ∫_c (e^(iπ) /((z^2 +4)^2 (z+1)^2 ))dz where c is a circle with ∣z−i∣=3.5 help please

$$\mathrm{Evaluate}\:\mathrm{using}\:\mathrm{cauchy}'\mathrm{s}\:\mathrm{integral}\: \\ $$$$\:\:\:\:\:\:\:\:\:\int_{\mathrm{c}} \:\frac{\mathrm{e}^{\mathrm{i}\pi} }{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dz} \\ $$$$\mathrm{where}\:\mathrm{c}\:\mathrm{is}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{with}\:\mid\mathrm{z}−\mathrm{i}\mid=\mathrm{3}.\mathrm{5} \\ $$$$ \\ $$$$\mathrm{help}\:\mathrm{please} \\ $$

Commented by mathmax by abdo last updated on 20/Mar/20

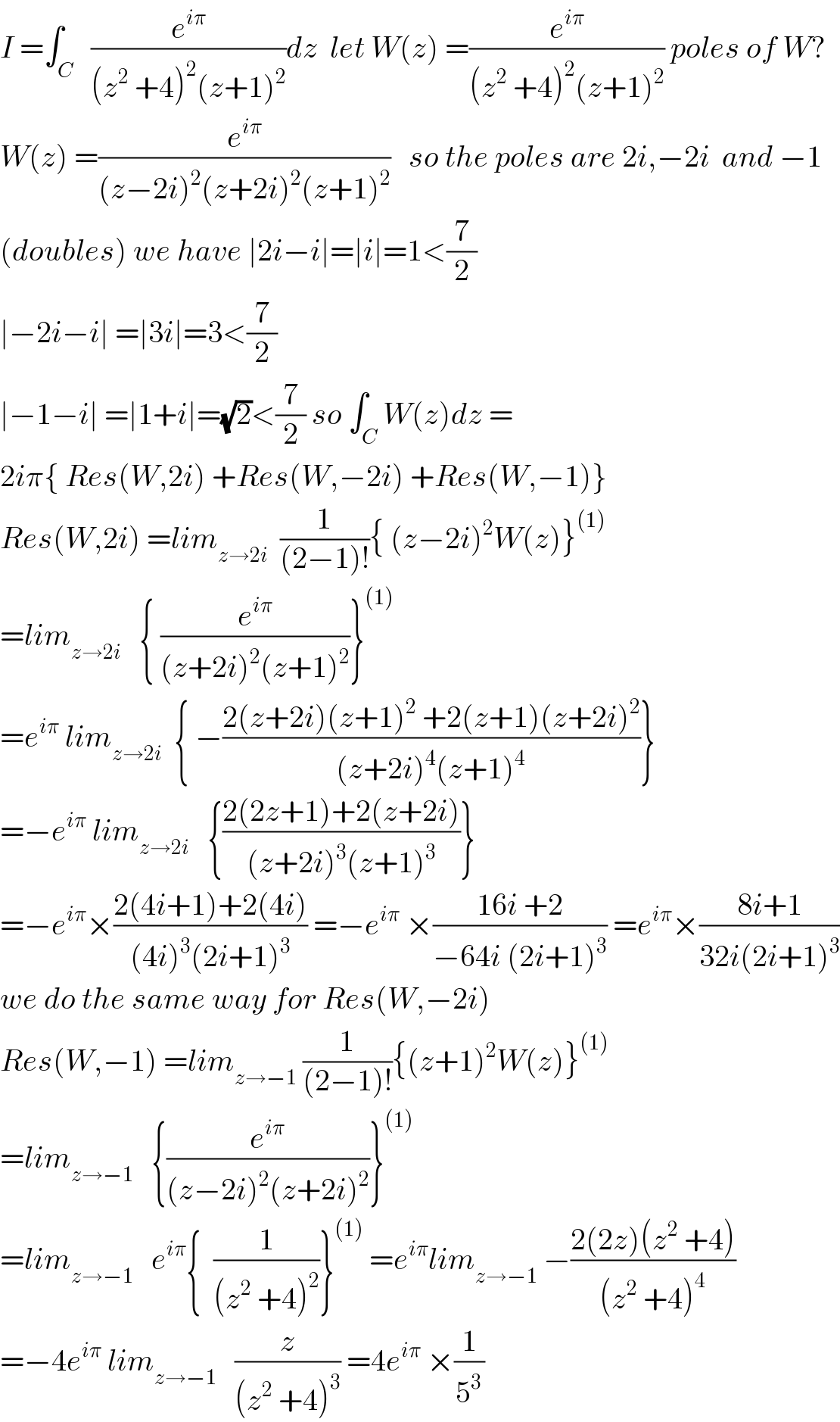
I =∫_C (e^(iπ) /((z^2 +4)^2 (z+1)^2 ))dz let W(z) =(e^(iπ) /((z^2 +4)^2 (z+1)^2 )) poles of W? W(z) =(e^(iπ) /((z−2i)^2 (z+2i)^2 (z+1)^2 )) so the poles are 2i,−2i and −1 (doubles) we have ∣2i−i∣=∣i∣=1<(7/2) ∣−2i−i∣ =∣3i∣=3<(7/2) ∣−1−i∣ =∣1+i∣=(√2)<(7/2) so ∫_C W(z)dz = 2iπ{ Res(W,2i) +Res(W,−2i) +Res(W,−1)} Res(W,2i) =lim_(z→2i) (1/((2−1)!)){ (z−2i)^2 W(z)}^((1)) =lim_(z→2i) { (e^(iπ) /((z+2i)^2 (z+1)^2 ))}^((1)) =e^(iπ) lim_(z→2i) { −((2(z+2i)(z+1)^2 +2(z+1)(z+2i)^2 )/((z+2i)^4 (z+1)^4 ))} =−e^(iπ) lim_(z→2i) {((2(2z+1)+2(z+2i))/((z+2i)^3 (z+1)^3 ))} =−e^(iπ) ×((2(4i+1)+2(4i))/((4i)^3 (2i+1)^3 )) =−e^(iπ) ×((16i +2)/(−64i (2i+1)^3 )) =e^(iπ) ×((8i+1)/(32i(2i+1)^3 )) we do the same way for Res(W,−2i) Res(W,−1) =lim_(z→−1) (1/((2−1)!)){(z+1)^2 W(z)}^((1)) =lim_(z→−1) {(e^(iπ) /((z−2i)^2 (z+2i)^2 ))}^((1)) =lim_(z→−1) e^(iπ) { (1/((z^2 +4)^2 ))}^((1)) =e^(iπ) lim_(z→−1) −((2(2z)(z^2 +4))/((z^2 +4)^4 )) =−4e^(iπ) lim_(z→−1) (z/((z^2 +4)^3 )) =4e^(iπ) ×(1/5^3 )

$${I}\:=\int_{{C}} \:\:\frac{{e}^{{i}\pi} }{\left({z}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} \left({z}+\mathrm{1}\right)^{\mathrm{2}} }{dz}\:\:{let}\:{W}\left({z}\right)\:=\frac{{e}^{{i}\pi} }{\left({z}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} \left({z}+\mathrm{1}\right)^{\mathrm{2}} }\:{poles}\:{of}\:{W}? \\ $$$${W}\left({z}\right)\:=\frac{{e}^{{i}\pi} }{\left({z}−\mathrm{2}{i}\right)^{\mathrm{2}} \left({z}+\mathrm{2}{i}\right)^{\mathrm{2}} \left({z}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:{so}\:{the}\:{poles}\:{are}\:\mathrm{2}{i},−\mathrm{2}{i}\:\:{and}\:−\mathrm{1} \\ $$$$\left({doubles}\right)\:{we}\:{have}\:\mid\mathrm{2}{i}−{i}\mid=\mid{i}\mid=\mathrm{1}<\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\mid−\mathrm{2}{i}−{i}\mid\:=\mid\mathrm{3}{i}\mid=\mathrm{3}<\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\mid−\mathrm{1}−{i}\mid\:=\mid\mathrm{1}+{i}\mid=\sqrt{\mathrm{2}}<\frac{\mathrm{7}}{\mathrm{2}}\:{so}\:\int_{{C}} {W}\left({z}\right){dz}\:= \\ $$$$\mathrm{2}{i}\pi\left\{\:{Res}\left({W},\mathrm{2}{i}\right)\:+{Res}\left({W},−\mathrm{2}{i}\right)\:+{Res}\left({W},−\mathrm{1}\right)\right\} \\ $$$${Res}\left({W},\mathrm{2}{i}\right)\:={lim}_{{z}\rightarrow\mathrm{2}{i}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\:\left({z}−\mathrm{2}{i}\right)^{\mathrm{2}} {W}\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow\mathrm{2}{i}} \:\:\:\left\{\:\frac{{e}^{{i}\pi} }{\left({z}+\mathrm{2}{i}\right)^{\mathrm{2}} \left({z}+\mathrm{1}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={e}^{{i}\pi} \:{lim}_{{z}\rightarrow\mathrm{2}{i}} \:\:\left\{\:−\frac{\mathrm{2}\left({z}+\mathrm{2}{i}\right)\left({z}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}\left({z}+\mathrm{1}\right)\left({z}+\mathrm{2}{i}\right)^{\mathrm{2}} }{\left({z}+\mathrm{2}{i}\right)^{\mathrm{4}} \left({z}+\mathrm{1}\right)^{\mathrm{4}} }\right\} \\ $$$$=−{e}^{{i}\pi} \:{lim}_{{z}\rightarrow\mathrm{2}{i}} \:\:\:\left\{\frac{\mathrm{2}\left(\mathrm{2}{z}+\mathrm{1}\right)+\mathrm{2}\left({z}+\mathrm{2}{i}\right)}{\left({z}+\mathrm{2}{i}\right)^{\mathrm{3}} \left({z}+\mathrm{1}\right)^{\mathrm{3}} }\right\} \\ $$$$=−{e}^{{i}\pi} ×\frac{\mathrm{2}\left(\mathrm{4}{i}+\mathrm{1}\right)+\mathrm{2}\left(\mathrm{4}{i}\right)}{\left(\mathrm{4}{i}\right)^{\mathrm{3}} \left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{3}} }\:=−{e}^{{i}\pi} \:×\frac{\mathrm{16}{i}\:+\mathrm{2}}{−\mathrm{64}{i}\:\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{3}} }\:={e}^{{i}\pi} ×\frac{\mathrm{8}{i}+\mathrm{1}}{\mathrm{32}{i}\left(\mathrm{2}{i}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${we}\:{do}\:{the}\:{same}\:{way}\:{for}\:{Res}\left({W},−\mathrm{2}{i}\right) \\ $$$${Res}\left({W},−\mathrm{1}\right)\:={lim}_{{z}\rightarrow−\mathrm{1}} \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}+\mathrm{1}\right)^{\mathrm{2}} {W}\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow−\mathrm{1}} \:\:\:\left\{\frac{{e}^{{i}\pi} }{\left({z}−\mathrm{2}{i}\right)^{\mathrm{2}} \left({z}+\mathrm{2}{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow−\mathrm{1}} \:\:\:{e}^{{i}\pi} \left\{\:\:\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \:={e}^{{i}\pi} {lim}_{{z}\rightarrow−\mathrm{1}} \:−\frac{\mathrm{2}\left(\mathrm{2}{z}\right)\left({z}^{\mathrm{2}} \:+\mathrm{4}\right)}{\left({z}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{4}} } \\ $$$$=−\mathrm{4}{e}^{{i}\pi} \:{lim}_{{z}\rightarrow−\mathrm{1}} \:\:\:\frac{{z}}{\left({z}^{\mathrm{2}} \:+\mathrm{4}\right)^{\mathrm{3}} }\:=\mathrm{4}{e}^{{i}\pi} \:×\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{3}} } \\ $$

Answered by mind is power last updated on 20/Mar/20

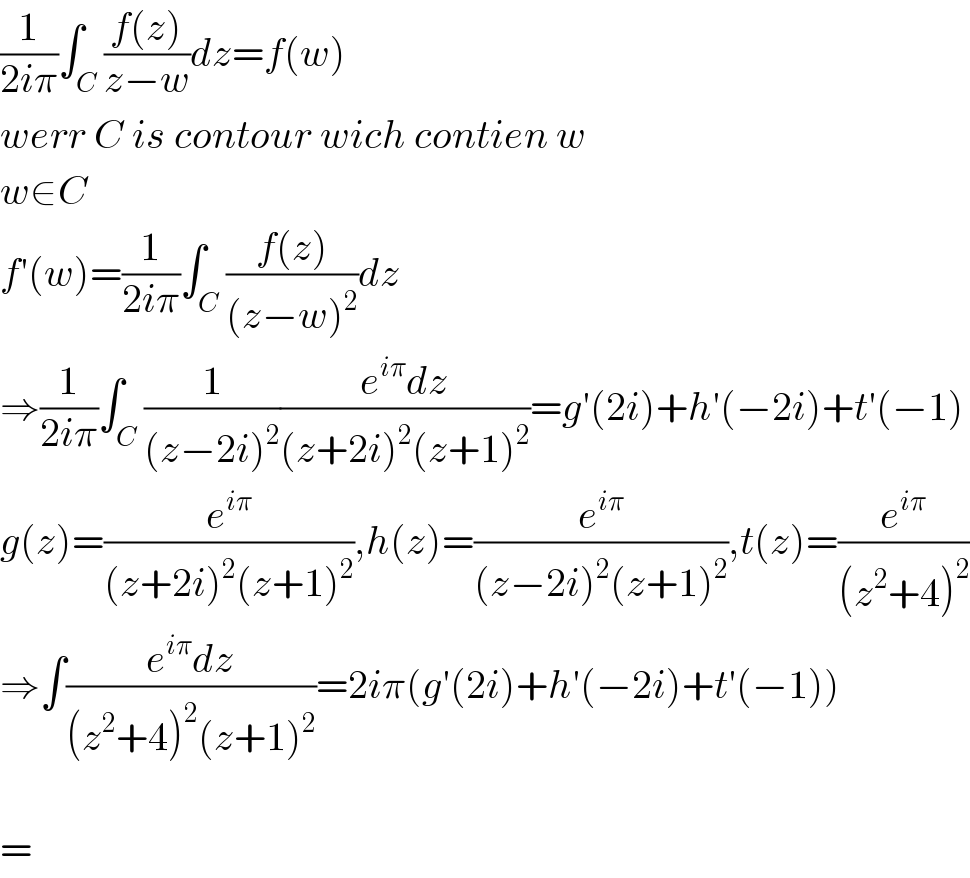
(1/(2iπ))∫_C ((f(z))/(z−w))dz=f(w) werr C is contour wich contien w w∈C f′(w)=(1/(2iπ))∫_C ((f(z))/((z−w)^2 ))dz ⇒(1/(2iπ))∫_C (1/((z−2i)^2 ))((e^(iπ) dz)/((z+2i)^2 (z+1)^2 ))=g′(2i)+h′(−2i)+t′(−1) g(z)=(e^(iπ) /((z+2i)^2 (z+1)^2 )),h(z)=(e^(iπ) /((z−2i)^2 (z+1)^2 )),t(z)=(e^(iπ) /((z^2 +4)^2 )) ⇒∫((e^(iπ) dz)/((z^2 +4)^2 (z+1)^2 ))=2iπ(g′(2i)+h′(−2i)+t′(−1)) =

$$\frac{\mathrm{1}}{\mathrm{2}{i}\pi}\int_{{C}} \frac{{f}\left({z}\right)}{{z}−{w}}{dz}={f}\left({w}\right) \\ $$$${werr}\:{C}\:{is}\:{contour}\:{wich}\:{contien}\:{w} \\ $$$${w}\in{C} \\ $$$${f}'\left({w}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}\pi}\int_{{C}} \frac{{f}\left({z}\right)}{\left({z}−{w}\right)^{\mathrm{2}} }{dz} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}{i}\pi}\int_{{C}} \frac{\mathrm{1}}{\left({z}−\mathrm{2}{i}\right)^{\mathrm{2}} }\frac{{e}^{{i}\pi} {dz}}{\left({z}+\mathrm{2}{i}\right)^{\mathrm{2}} \left({z}+\mathrm{1}\right)^{\mathrm{2}} }={g}'\left(\mathrm{2}{i}\right)+{h}'\left(−\mathrm{2}{i}\right)+{t}'\left(−\mathrm{1}\right) \\ $$$${g}\left({z}\right)=\frac{{e}^{{i}\pi} }{\left({z}+\mathrm{2}{i}\right)^{\mathrm{2}} \left({z}+\mathrm{1}\right)^{\mathrm{2}} },{h}\left({z}\right)=\frac{{e}^{{i}\pi} }{\left({z}−\mathrm{2}{i}\right)^{\mathrm{2}} \left({z}+\mathrm{1}\right)^{\mathrm{2}} },{t}\left({z}\right)=\frac{{e}^{{i}\pi} }{\left({z}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\int\frac{{e}^{{i}\pi} {dz}}{\left({z}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} \left({z}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{2}{i}\pi\left({g}'\left(\mathrm{2}{i}\right)+{h}'\left(−\mathrm{2}{i}\right)+{t}'\left(−\mathrm{1}\right)\right) \\ $$$$ \\ $$$$= \\ $$

Commented by Umar last updated on 20/Mar/20

thanks

$$\mathrm{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com