Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 85456 by jagoll last updated on 22/Mar/20

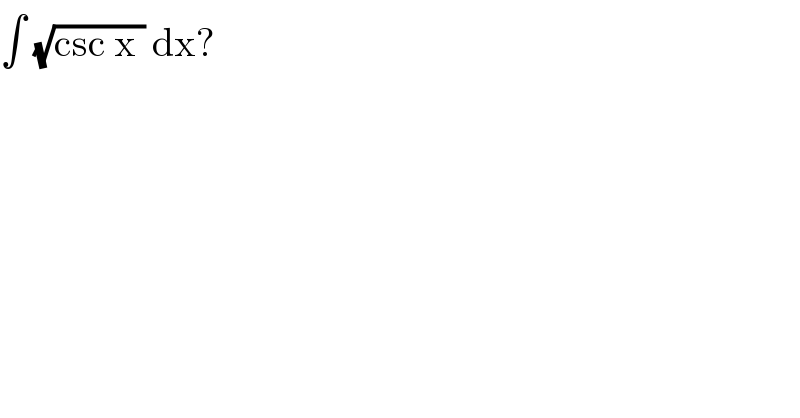
∫ (√(csc x )) dx?

$$\int\:\sqrt{\mathrm{csc}\:\mathrm{x}\:}\:\mathrm{dx}? \\ $$

Commented by jagoll last updated on 22/Mar/20

thank sir

$$\mathrm{thank}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 22/Mar/20

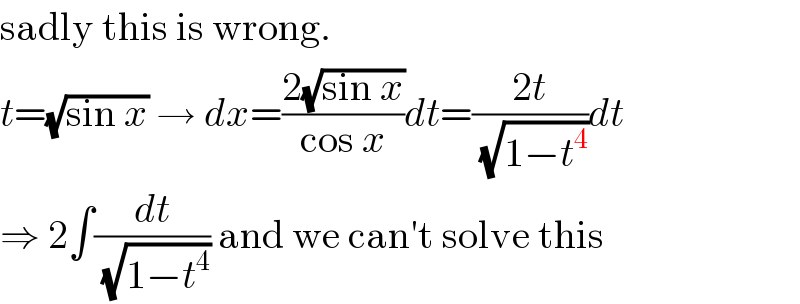
sadly this is wrong. t=(√(sin x)) → dx=((2(√(sin x)))/(cos x))dt=((2t)/(√(1−t^4 )))dt ⇒ 2∫(dt/(√(1−t^4 ))) and we can′t solve this

$$\mathrm{sadly}\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong}. \\ $$$${t}=\sqrt{\mathrm{sin}\:{x}}\:\rightarrow\:{dx}=\frac{\mathrm{2}\sqrt{\mathrm{sin}\:{x}}}{\mathrm{cos}\:{x}}{dt}=\frac{\mathrm{2}{t}}{\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}{dt} \\ $$$$\Rightarrow\:\mathrm{2}\int\frac{{dt}}{\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}\:\mathrm{and}\:\mathrm{we}\:\mathrm{can}'\mathrm{t}\:\mathrm{solve}\:\mathrm{this} \\ $$

Commented by MJS last updated on 22/Mar/20

you should always test your solutions (d/dx)[2arcsin (√(sin x))]=((cos x)/(√(sin x −sin^2 x)))≠(1/(√(sin x)))

$$\mathrm{you}\:\mathrm{should}\:{always}\:\mathrm{test}\:\mathrm{your}\:\mathrm{solutions} \\ $$$$\frac{{d}}{{dx}}\left[\mathrm{2arcsin}\:\sqrt{\mathrm{sin}\:{x}}\right]=\frac{\mathrm{cos}\:{x}}{\sqrt{\mathrm{sin}\:{x}\:−\mathrm{sin}^{\mathrm{2}} \:{x}}}\neq\frac{\mathrm{1}}{\sqrt{\mathrm{sin}\:{x}}} \\ $$

Commented by jagoll last updated on 22/Mar/20

so what the correct answer sir?

$$\mathrm{so}\:\mathrm{what}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{answer}\:\mathrm{sir}? \\ $$

Commented by MJS last updated on 22/Mar/20

I cannot solve it there′s a solution using Γ(x) somehow, it had been on this forum, maybe a year ago, I can′t find it

$$\mathrm{I}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{it} \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{using}\:\Gamma\left({x}\right)\:\mathrm{somehow},\:\mathrm{it}\:\mathrm{had} \\ $$$$\mathrm{been}\:\mathrm{on}\:\mathrm{this}\:\mathrm{forum},\:\mathrm{maybe}\:\mathrm{a}\:\mathrm{year}\:\mathrm{ago},\:\mathrm{I}\:\mathrm{can}'\mathrm{t} \\ $$$$\mathrm{find}\:\mathrm{it} \\ $$

Commented by jagoll last updated on 22/Mar/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 22/Mar/20

found this: ∫(dx/(√(sin x)))= [t=x−(π/2) → dx=dt] ∫(dt/(√(cos t)))=∫(dt/(√(1−2sin^2 (t/2))))= =F ((t/2)∣2) =F ((x/2)−(π/4)∣2) +C it′s an eliptic integral but I cannot explain, it′s not my solution

$$\mathrm{found}\:\mathrm{this}: \\ $$$$\int\frac{{dx}}{\sqrt{\mathrm{sin}\:{x}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}−\frac{\pi}{\mathrm{2}}\:\rightarrow\:{dx}={dt}\right] \\ $$$$\int\frac{{dt}}{\sqrt{\mathrm{cos}\:{t}}}=\int\frac{{dt}}{\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\frac{{t}}{\mathrm{2}}}}= \\ $$$$=\mathrm{F}\:\left(\frac{{t}}{\mathrm{2}}\mid\mathrm{2}\right)\:=\mathrm{F}\:\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\mid\mathrm{2}\right)\:+{C} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{an}\:\mathrm{eliptic}\:\mathrm{integral} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{cannot}\:\mathrm{explain},\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{my}\:\mathrm{solution} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com