Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 8554 by Sopheak last updated on 16/Oct/16

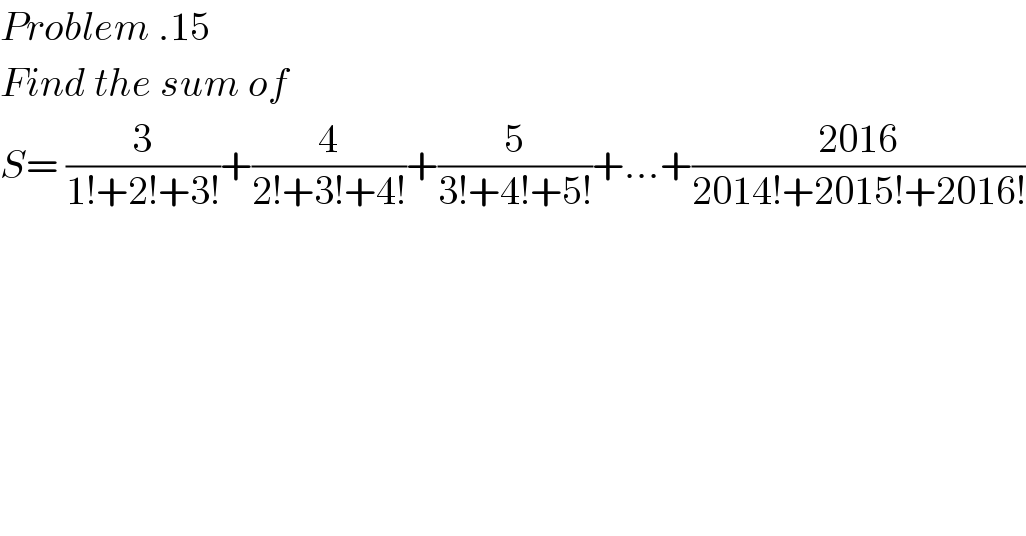
Problem .15 Find the sum of S= (3/(1!+2!+3!))+(4/(2!+3!+4!))+(5/(3!+4!+5!))+...+((2016)/(2014!+2015!+2016!))

$${Problem}\:.\mathrm{15} \\ $$$${Find}\:{the}\:{sum}\:{of} \\ $$$${S}=\:\frac{\mathrm{3}}{\mathrm{1}!+\mathrm{2}!+\mathrm{3}!}+\frac{\mathrm{4}}{\mathrm{2}!+\mathrm{3}!+\mathrm{4}!}+\frac{\mathrm{5}}{\mathrm{3}!+\mathrm{4}!+\mathrm{5}!}+...+\frac{\mathrm{2016}}{\mathrm{2014}!+\mathrm{2015}!+\mathrm{2016}!} \\ $$$$\: \\ $$

Commented by Yozzias last updated on 16/Oct/16

(3/(1!(1+2+2×3))),(4/(2!(1+3+3×4))),(5/(3!(1+4+4×5))),... ((n+2)/(n!(1+n+1+(n+1)(n+2)))) =((n+2)/(n!(2+n+n^2 +3n+2))) =((n+2)/(n!(4+4n+n^2 ))) =((n+2)/(n!(n+2)^2 )) =(1/(n!(n+2))) S=Σ_(r=1) ^n (1/(r!(r+2)))=Σ_(r=1) ^n ((r+1)/((r+2)!))=Σ_(r=1) ^(n+1) (r/((r+1)!))−(1/((1+1)!))=1−(1/((n+2)!))−(1/2) S=(1/2)−(1/((n+2)!)) n=2014⇒S=(1/2)−(1/(2016!)) Σ_(r=1) ^(2014) ((r+2)/(r!+(r+1)!+(r+2)!))=(1/2)−(1/(2016!))

$$\frac{\mathrm{3}}{\mathrm{1}!\left(\mathrm{1}+\mathrm{2}+\mathrm{2}×\mathrm{3}\right)},\frac{\mathrm{4}}{\mathrm{2}!\left(\mathrm{1}+\mathrm{3}+\mathrm{3}×\mathrm{4}\right)},\frac{\mathrm{5}}{\mathrm{3}!\left(\mathrm{1}+\mathrm{4}+\mathrm{4}×\mathrm{5}\right)},... \\ $$$$\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}!\left(\mathrm{1}+\mathrm{n}+\mathrm{1}+\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)\right)} \\ $$$$=\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}!\left(\mathrm{2}+\mathrm{n}+\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}!\left(\mathrm{4}+\mathrm{4n}+\mathrm{n}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}!\left(\mathrm{n}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}!\left(\mathrm{n}+\mathrm{2}\right)} \\ $$$$\mathrm{S}=\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{r}!\left(\mathrm{r}+\mathrm{2}\right)}=\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{r}+\mathrm{1}}{\left(\mathrm{r}+\mathrm{2}\right)!}=\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\frac{\mathrm{r}}{\left(\mathrm{r}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{1}\right)!}=\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{2}\right)!}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{S}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{2}\right)!} \\ $$$$\mathrm{n}=\mathrm{2014}\Rightarrow\mathrm{S}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2016}!} \\ $$$$\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{2014}} {\sum}}\frac{\mathrm{r}+\mathrm{2}}{\mathrm{r}!+\left(\mathrm{r}+\mathrm{1}\right)!+\left(\mathrm{r}+\mathrm{2}\right)!}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2016}!} \\ $$

Answered by Yozzias last updated on 16/Oct/16

Check answer in comments.

$$\mathrm{Check}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{comments}. \\ $$

Commented by Sopheak last updated on 16/Oct/16

Right answer

$${Right}\:{answer} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com