Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 85542 by TawaTawa1 last updated on 22/Mar/20

Commented by TawaTawa1 last updated on 22/Mar/20

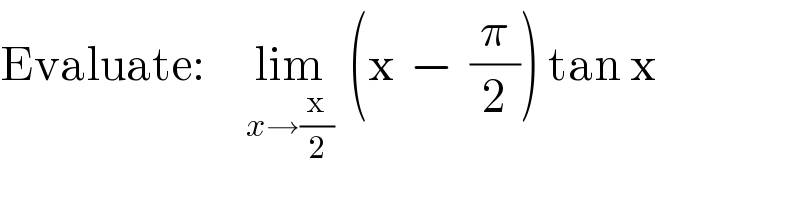
Evaluate: lim_(x→(x/2)) (x − (π/2)) tan x

$$\mathrm{Evaluate}:\:\:\:\:\:\underset{{x}\rightarrow\frac{\mathrm{x}}{\mathrm{2}}} {\mathrm{lim}}\:\:\left(\mathrm{x}\:\:−\:\:\frac{\pi}{\mathrm{2}}\right)\:\mathrm{tan}\:\mathrm{x} \\ $$

Commented by mathmax by abdo last updated on 22/Mar/20

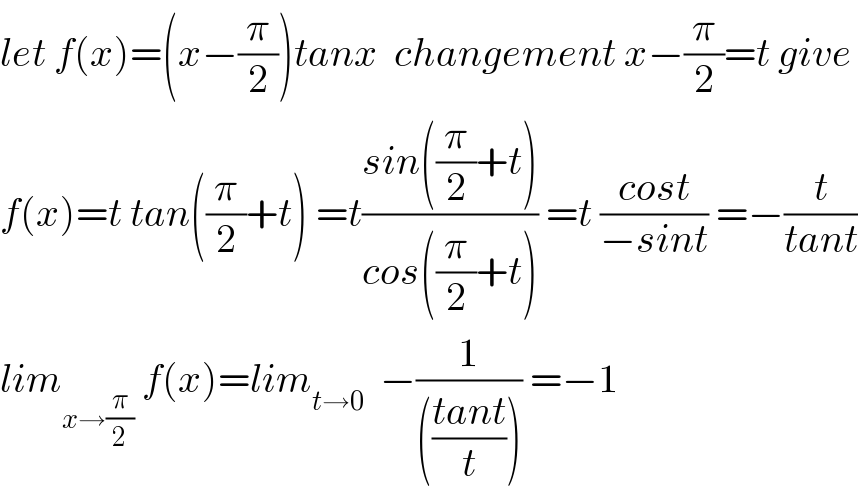
let f(x)=(x−(π/2))tanx changement x−(π/2)=t give f(x)=t tan((π/2)+t) =t((sin((π/2)+t))/(cos((π/2)+t))) =t ((cost)/(−sint)) =−(t/(tant)) lim_(x→(π/2)) f(x)=lim_(t→0) −(1/((((tant)/t)))) =−1

$${let}\:{f}\left({x}\right)=\left({x}−\frac{\pi}{\mathrm{2}}\right){tanx}\:\:{changement}\:{x}−\frac{\pi}{\mathrm{2}}={t}\:{give} \\ $$$${f}\left({x}\right)={t}\:{tan}\left(\frac{\pi}{\mathrm{2}}+{t}\right)\:={t}\frac{{sin}\left(\frac{\pi}{\mathrm{2}}+{t}\right)}{{cos}\left(\frac{\pi}{\mathrm{2}}+{t}\right)}\:={t}\:\frac{{cost}}{−{sint}}\:=−\frac{{t}}{{tant}} \\ $$$${lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:{f}\left({x}\right)={lim}_{{t}\rightarrow\mathrm{0}} \:\:−\frac{\mathrm{1}}{\left(\frac{{tant}}{{t}}\right)}\:=−\mathrm{1} \\ $$

Commented by TawaTawa1 last updated on 22/Mar/20

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by turbo msup by abdo last updated on 23/Mar/20

you are welcome miss tawa

$${you}\:{are}\:{welcome}\:{miss}\:{tawa} \\ $$

Answered by jagoll last updated on 22/Mar/20

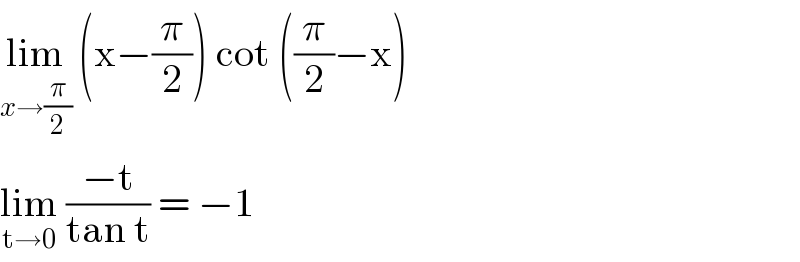
lim_(x→(π/2)) (x−(π/2)) cot ((π/2)−x) lim_(t→0) ((−t)/(tan t)) = −1

$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\left(\mathrm{x}−\frac{\pi}{\mathrm{2}}\right)\:\mathrm{cot}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right) \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{t}}{\mathrm{tan}\:\mathrm{t}}\:=\:−\mathrm{1} \\ $$

Commented by TawaTawa1 last updated on 22/Mar/20

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by TawaTawa1 last updated on 22/Mar/20

Sir, help me solve question 85546

$$\mathrm{Sir},\:\mathrm{help}\:\mathrm{me}\:\mathrm{solve}\:\mathrm{question}\:\:\mathrm{85546} \\ $$

Commented by jagoll last updated on 23/Mar/20

writting is too small, i did not clearly read it

$$\mathrm{writting}\:\mathrm{is}\:\mathrm{too}\:\mathrm{small},\:\mathrm{i}\:\mathrm{did}\:\mathrm{not} \\ $$$$\mathrm{clearly}\:\mathrm{read}\:\mathrm{it} \\ $$

Commented by TawaTawa1 last updated on 23/Mar/20

Thank you sir, please check, i retype.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{please}\:\mathrm{check},\:\mathrm{i}\:\mathrm{retype}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com