∫ _0 ^(2π) (dx/((√2)−cos x))


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 85568 by jagoll last updated on 23/Mar/20

$\int \underset{0}{\overset{2 π}{}} \frac{dx}{\sqrt{2} - \cos x}$
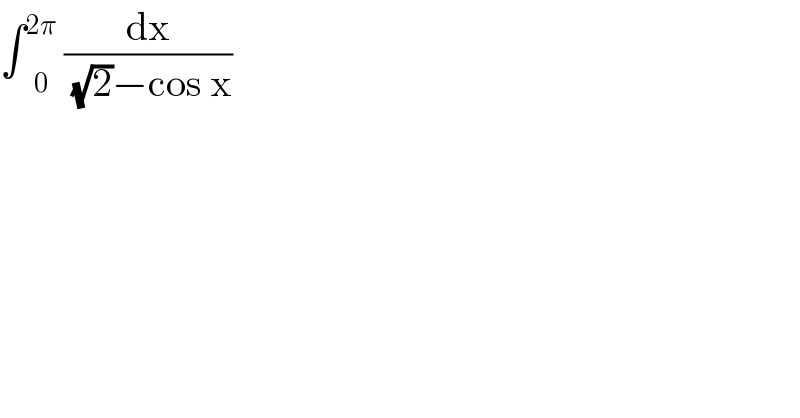
Commented by jagoll last updated on 23/Mar/20

$I = \int \underset{0}{\overset{2 π}{}} \frac{dx}{\sqrt{2} - \cos x}$ $let x = 2 π - t$ $I = \int \underset{2 π}{\overset{0}{}} \frac{- dt}{\sqrt{2} - \cos (2 π - t)}$ $I = \int \underset{0}{\overset{2 π}{}} \frac{dt}{\sqrt{2} - \cos t}$ $I = I (not valid)$
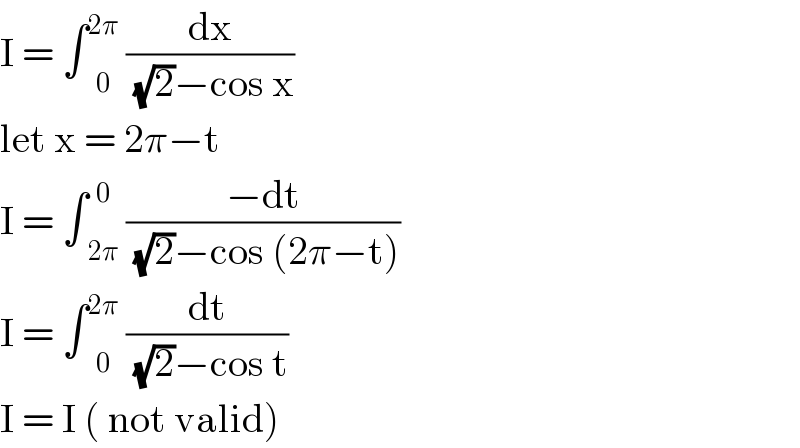
Commented by mathmax by abdo last updated on 23/Mar/20

$A = \int_{0}^{2 π} \frac{d x}{\sqrt{2} - c o s x} \Rightarrow A = \int_{0}^{2 π} \frac{d x}{\sqrt{2} - \frac{e^{i x} + e^{- i x}}{2}}$ $= \int_{0}^{2 π} \frac{2 d x}{2 \sqrt{2} - e^{i x} - e^{- i x}} =_{e^{i x} = z} \int_{∣ z ∣= 1} \frac{2}{2 \sqrt{2} - z - z^{- 1}} \frac{d z}{i z}$ $= \int_{∣ z ∣= 1} \frac{- 2 i d z}{2 \sqrt{2} z - z^{2} - 1} = \int_{∣ z ∣= 1} \frac{2 i d z}{z^{2} - 2 \sqrt{2} z + 1} = \int_{∣ z ∣= 1} φ (z) d z$ $w i t h φ (z) = \frac{2 i}{z^{2} - 2 \sqrt{2} z + 1} p o l e s o f φ ?$ $z^{2} - 2 \sqrt{2} z + 1 = 0 \to Δ^{^{'}} = 2 - 1 = 1 \Rightarrow z_{1} = 1 + \sqrt{2} a n d z_{2} = - 1 + \sqrt{2}$ $\Rightarrow φ (z) = \frac{2 i}{(z - z_{1}) (z - z_{2})}$ $∣ z_{1} ∣ - 1 = 1 + \sqrt{2} - 1 > 0 (o u t o f c i r c l e)$ $∣ z_{2} ∣ - 1 =∣ \sqrt{2} - 1 ∣ - 1 = \sqrt{2} - 2 < 0 \Rightarrow$ $\int_{∣ z ∣= 1} φ (z) d z = 2 i π R e s (φ, z_{2}) = 2 i π \times \frac{2 i}{(z_{2} - z_{1})} = \frac{- 4 π}{- 2} = 2 π$ $\Rightarrow A = 2 π$
	Answered by mind is power last updated on 23/Mar/20
	$=∫_0 ^π (dx/((√2)−cos(x)))+∫_π ^(2π) (dx/((√2)−cos(x))) t=π+x in 2nd⇒ =∫_0 ^π (dx/((√2)−cos(x)))+(dx/((√2)+cos(x))) =∫_0 ^π ((2(√2)dx)/(2−cos^2 (x)))=2(√2)∫_0 ^(π/2) (dx/(2−cos^2 (x)))+2(√2)∫_(π/2) ^π (dx/(2−cos^2 (x))) t=(π/2)+x in 2nd ⇒=2(√(2{))∫_0 ^(π/2) (dx/(1+sin^2 (x)))+∫_0 ^(π/2) (dx/(1+cos^2 ((x/2)))) =2(√2)∫_0 ^(π/2) (1/(sin^2 (x))).((dx/((1/(sin^2 (x)))+1)))+2(√2)∫_0 ^(π/2) (dx/(cos^2 (x))).(1/(((1/(cos^2 (x)))+1))) =2(√2)∫_0 ^(π/2) ((−d(cot(x)))/(2+cot^2 (x)))+2(√2)∫_0 ^(π/2) ((d(tg(x)))/(2+tg^2 (x))) =2([_0 ^(π/2) −arctan(((cot(x))/(√2)))+arctan(((tg(x))/(√2)))) =2.(π/2)+2.(π/2)=2π$
	$= \int_{0}^{π} \frac{d x}{\sqrt{2} - c o s (x)} + \int_{π}^{2 π} \frac{d x}{\sqrt{2} - c o s (x)}$ $t = π + x i n 2 n d \Rightarrow$ $= \int_{0}^{π} \frac{d x}{\sqrt{2} - c o s (x)} + \frac{d x}{\sqrt{2} + c o s (x)}$ $= \int_{0}^{π} \frac{2 \sqrt{2} d x}{2 - {c o s}^{2} (x)} = 2 \sqrt{2} \int_{0}^{\frac{π}{2}} \frac{d x}{2 - {c o s}^{2} (x)} + 2 \sqrt{2} \int_{\frac{π}{2}}^{π} \frac{d x}{2 - {c o s}^{2} (x)}$ $t = \frac{π}{2} + x i n 2 n d$ $\Rightarrow= 2 \sqrt{2 {} \int_{0}^{\frac{π}{2}} \frac{d x}{1 + {s i n}^{2} (x)} + \int_{0}^{\frac{π}{2}} \frac{d x}{1 + {c o s}^{2} (\frac{x}{2})}$ $= 2 \sqrt{2} \int_{0}^{\frac{π}{2}} \frac{1}{{s i n}^{2} (x)} . (\frac{d x}{\frac{1}{{s i n}^{2} (x)} + 1}) + 2 \sqrt{2} \int_{0}^{\frac{π}{2}} \frac{d x}{{c o s}^{2} (x)} . \frac{1}{(\frac{1}{{c o s}^{2} (x)} + 1)}$ $= 2 \sqrt{2} \int_{0}^{\frac{π}{2}} \frac{- d (c o t (x))}{2 + {c o t}^{2} (x)} + 2 \sqrt{2} \int_{0}^{\frac{π}{2}} \frac{d (t g (x))}{2 + {t g}^{2} (x)}$ $= 2 ([_{0}^{\frac{π}{2}} - a r c t a n (\frac{c o t (x)}{\sqrt{2}}) + a r c t a n (\frac{t g (x)}{\sqrt{2}}))$ $= 2 . \frac{π}{2} + 2 . \frac{π}{2} = 2 π$
	Commented by jagoll last updated on 23/Mar/20

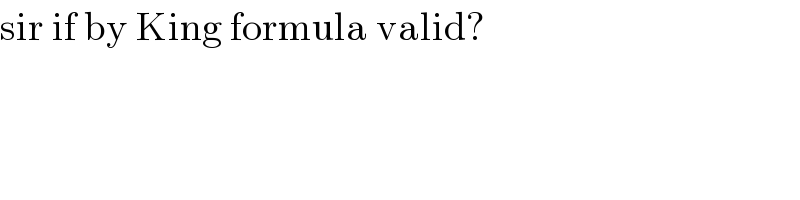
	$sir if by King formula valid ?$
	Commented by mind is power last updated on 23/Mar/20

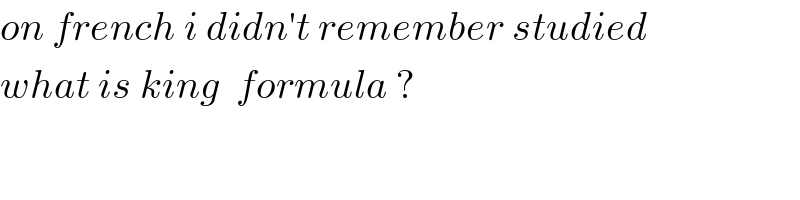
	$o n f r e n c h i {d i d n}^{'} t r e m e m b e r s t u d i e d$ $w h a t i s k i n g f o r m u l a ?$
	Answered by mind is power last updated on 23/Mar/20

	$= \int_{0}^{2 π} \frac{2 d x}{2 \sqrt{2} - (e^{i x} + e^{- i x})}$ $2 n d W a y$ $= \int_{0}^{2 π} \frac{2 e^{i x}}{- e^{2 i x} + 2 \sqrt{2} e^{i x} - 1}$ $e^{i x} = z \Rightarrow$ $= \int_{C} \frac{2 i d z}{(z - (\sqrt{2} - 1)) (z - (\sqrt{2} + 1))}$ $o n l y \sqrt{2} - 1 \in D (0, 1)$ $= 2 i π . \lim_{z \to \sqrt{2} - 1} (z - (\sqrt{2} - 1)) \frac{2 i}{(z - (\sqrt{2} - 1)) (z - (\sqrt{2} + 1))}$ $= 2 i π . \frac{2 i}{- 2} = 2 π$
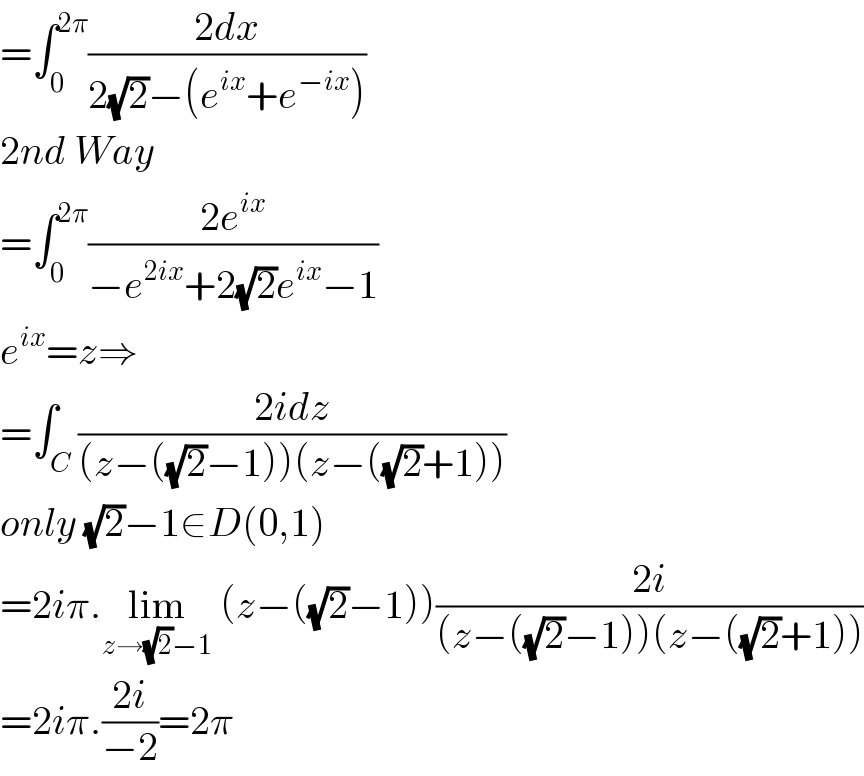
	Answered by mind is power last updated on 23/Mar/20

	$y o u c a n a l w a y s d o l v e \int \frac{p (s i n (t), c o s (t))}{Q (s i n (t), c o s (t))} d t$ $w i t h e P s n d Q \in R [x] [y]$ $b y t g (\frac{t}{2}) = x$
	Commented by jagoll last updated on 23/Mar/20

	$oo yes weirstrass sir$
	Answered by MJS last updated on 23/Mar/20

	$\int \frac{d x}{\sqrt{2} - \cos x} =$ $[t = \tan \frac{x}{2} \to d x = \frac{2}{t^{2} + 1} d t]$ $= - 2 (1 - \sqrt{2}) \int \frac{d t}{t^{2} + 3 - 2 \sqrt{2}} =$ $= 2 \arctan ((1 + \sqrt{2}) t) =$ $= 2 \arctan ((1 + \sqrt{2}) \tan \frac{x}{2}) + C$
	Commented by jagoll last updated on 23/Mar/20

	$sir if x = 0 \Rightarrow t = 0$ $if x = 2 π \Rightarrow t = 0$ $does mean : 2 \sqrt{2} - 1 \int_{0}^{0} \frac{dt}{t^{2} + 3 - 2 \sqrt{2}}$ $= 0 ?$ $what wrong sir ?$
	Commented by MJS last updated on 23/Mar/20

	$the given function is symmetric about x = π$ $\Rightarrow \underset{0}{\int^{2 π}} f (x) d x = 2 \underset{0}{\int^{π}} f (x) d x$
	Commented by MJS last updated on 23/Mar/20

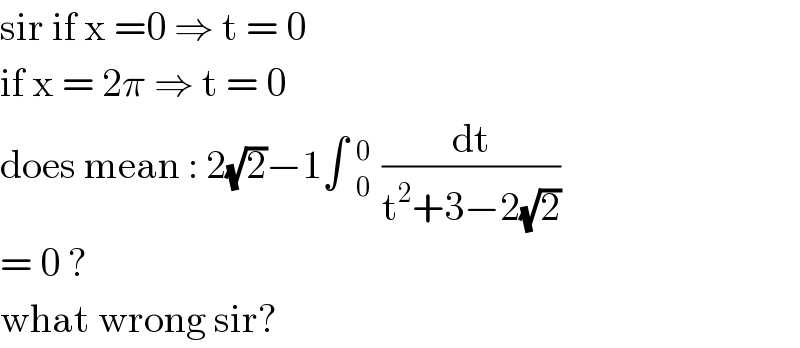
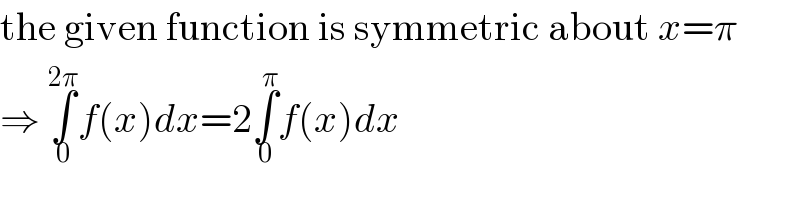
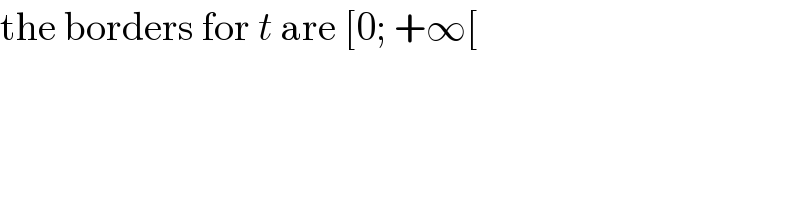
	$the borders for t are [0; + \infty [$
	Commented by jagoll last updated on 23/Mar/20

	$Missing \left or extra \right$ $4 \times [arc \tan ((1 + \sqrt{2}) \tan \frac{π}{4})]$ $4 \times [arc \tan ((1 + \sqrt{2}))] ?$
	Commented by jagoll last updated on 23/Mar/20

	$please sir . completely your answer$ $sir$
	Commented by jagoll last updated on 23/Mar/20

	$Missing \left or extra \right$ $4 \times [arc \tan (\infty) - arc \tan (0)]$ $4 \times \frac{π}{2} = 2 π$
	Commented by MJS last updated on 23/Mar/20

	$\underset{0}{\int^{2 π}} \frac{d x}{\sqrt{2} - \cos x} = 2 \underset{0}{\int^{π}} \frac{d x}{\sqrt{2} - \cos x} =$ $= 2 {[2 \arctan ((1 + \sqrt{2}) \tan \frac{x}{2})]}_{0}^{π} =$ $= 4 \lim_{x \to π^{-}} (\arctan ((1 + \sqrt{2}) \tan \frac{x}{2})) = 4 \times \frac{π}{2} = 2 π$
	Commented by jagoll last updated on 23/Mar/20

	$thank you sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum