Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 8558 by Sopheak last updated on 16/Oct/16

Commented by FilupSmith last updated on 16/Oct/16

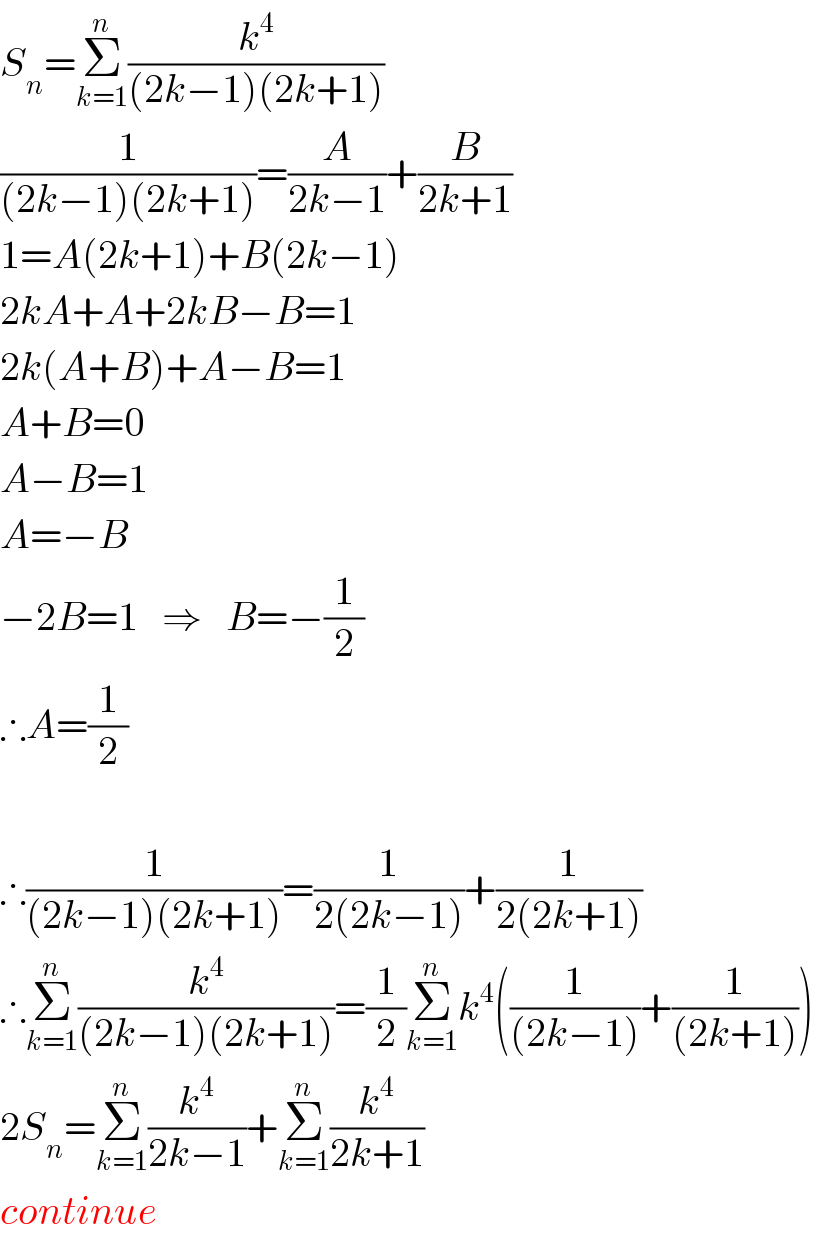
S_n =Σ_(k=1) ^n (k^4 /((2k−1)(2k+1))) (1/((2k−1)(2k+1)))=(A/(2k−1))+(B/(2k+1)) 1=A(2k+1)+B(2k−1) 2kA+A+2kB−B=1 2k(A+B)+A−B=1 A+B=0 A−B=1 A=−B −2B=1 ⇒ B=−(1/2) ∴A=(1/2) ∴(1/((2k−1)(2k+1)))=(1/(2(2k−1)))+(1/(2(2k+1))) ∴Σ_(k=1) ^n (k^4 /((2k−1)(2k+1)))=(1/2)Σ_(k=1) ^n k^4 ((1/((2k−1)))+(1/((2k+1)))) 2S_n =Σ_(k=1) ^n (k^4 /(2k−1))+Σ_(k=1) ^n (k^4 /(2k+1)) continue

$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{4}} }{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}=\frac{{A}}{\mathrm{2}{k}−\mathrm{1}}+\frac{{B}}{\mathrm{2}{k}+\mathrm{1}} \\ $$$$\mathrm{1}={A}\left(\mathrm{2}{k}+\mathrm{1}\right)+{B}\left(\mathrm{2}{k}−\mathrm{1}\right) \\ $$$$\mathrm{2}{kA}+{A}+\mathrm{2}{kB}−{B}=\mathrm{1} \\ $$$$\mathrm{2}{k}\left({A}+{B}\right)+{A}−{B}=\mathrm{1} \\ $$$${A}+{B}=\mathrm{0} \\ $$$${A}−{B}=\mathrm{1} \\ $$$${A}=−{B} \\ $$$$−\mathrm{2}{B}=\mathrm{1}\:\:\:\Rightarrow\:\:\:{B}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\therefore{A}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\: \\ $$$$\therefore\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{k}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$\therefore\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{4}} }{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{4}} \left(\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)}\right) \\ $$$$\mathrm{2}{S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{4}} }{\mathrm{2}{k}−\mathrm{1}}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{4}} }{\mathrm{2}{k}+\mathrm{1}} \\ $$$${continue} \\ $$

Commented by FilupSmith last updated on 16/Oct/16

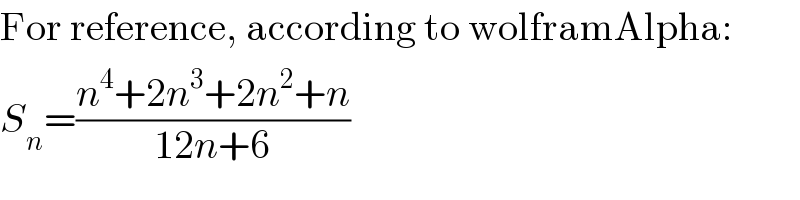
For reference, according to wolframAlpha: S_n =((n^4 +2n^3 +2n^2 +n)/(12n+6))

$$\mathrm{For}\:\mathrm{reference},\:\mathrm{according}\:\mathrm{to}\:\mathrm{wolframAlpha}: \\ $$$${S}_{{n}} =\frac{{n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}}{\mathrm{12}{n}+\mathrm{6}} \\ $$

Commented by prakash jain last updated on 16/Oct/16

(k^4 /((2k−1)(2k+1)))=(1/(16))[((16k^4 −1+1)/((2k−1)(2k+1)))] =(1/(16))[(((4k^2 −1)(4k^2 +1))/((2k−1)(2k+1)))+(1/((2k−1)(2k+1)))] =(1/(16))[4k^2 +1+(1/2)((1/(2k−1))−(1/(2k+1)))] Σ_(k=1) ^n (k^4 /((2k−1)(2k+1)))=(1/(16))Σ_(k=1) ^n 4k^2 +(1/(16))Σ_(k=1) ^n 1 +Σ_(k=1) ^n ((1/(2k−1))−(1/(2k+1))) Σ_(k=1) ^n ((1/(2k−1))−(1/(2k+1)))=(1/1)−(1/3)+(1/3)−(1/5)..+(1/(2n−1))−(1/(2n+1)) =1−(1/(2n+1))=((2n)/(2n+1)) (1/(32))Σ_(k=1) ^n ((1/(2k−1))−(1/(2k+1)))=(n/(16(2n+1))) (1/(16))Σ_(k=1) ^n 4k^2 =((n(n+1)(2n+1))/(24)) (1/(16))Σ_(k=1) ^n 1=(n/(16)) Σ_(k=1) ^n (k^4 /((2k−1)(2k+1)))=((n(n+1)(2n+1))/(24))+(n/(16))+(1/(16))((n/(2n+1))) =((2n(n+1)(2n+1)^2 +3n(2n+1)+3n)/(48(2n+1))) =(((2n^2 +2n)(4n^2 +4n+1)+(6n^2 +3n)+3n)/(48(2n+1))) =((8n^4 +8n^3 +8n^3 +8n^2 +2n^2 +2n+6n^2 +3n+3n)/(48(2n+1))) =((8n^4 +16n^3 +16n^2 +8n)/(48(2n+1)))=((n^4 +2n^3 +2n^2 +n)/(6(2n+1)))

$$\frac{{k}^{\mathrm{4}} }{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{16}}\left[\frac{\mathrm{16}{k}^{\mathrm{4}} −\mathrm{1}+\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left[\frac{\left(\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4}{k}^{\mathrm{2}} +\mathrm{1}\right)}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left[\mathrm{4}{k}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right)\right] \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{4}} }{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{16}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{4}{k}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{16}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right) \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}..+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}=\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{32}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right)=\frac{{n}}{\mathrm{16}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{4}{k}^{\mathrm{2}} =\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{24}} \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1}=\frac{{n}}{\mathrm{16}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{4}} }{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{24}}+\frac{{n}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{16}}\left(\frac{{n}}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{2}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}{n}\left(\mathrm{2}{n}+\mathrm{1}\right)+\mathrm{3}{n}}{\mathrm{48}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$ \\ $$$$=\frac{\left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}\right)\left(\mathrm{4}{n}^{\mathrm{2}} +\mathrm{4}{n}+\mathrm{1}\right)+\left(\mathrm{6}{n}^{\mathrm{2}} +\mathrm{3}{n}\right)+\mathrm{3}{n}}{\mathrm{48}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{8}{n}^{\mathrm{4}} +\mathrm{8}{n}^{\mathrm{3}} +\mathrm{8}{n}^{\mathrm{3}} +\mathrm{8}{n}^{\mathrm{2}} +\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{6}{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{3}{n}}{\mathrm{48}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{8}{n}^{\mathrm{4}} +\mathrm{16}{n}^{\mathrm{3}} +\mathrm{16}{n}^{\mathrm{2}} +\mathrm{8}{n}}{\mathrm{48}\left(\mathrm{2}{n}+\mathrm{1}\right)}=\frac{{n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{3}} +\mathrm{2}{n}^{\mathrm{2}} +{n}}{\mathrm{6}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$

Answered by prakash jain last updated on 16/Oct/16

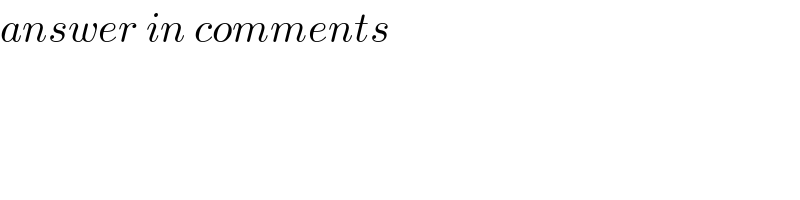
answer in comments

$${answer}\:{in}\:{comments} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com