
Question and Answers Forum
Question Number 85596 by M±th+et£s last updated on 23/Mar/20
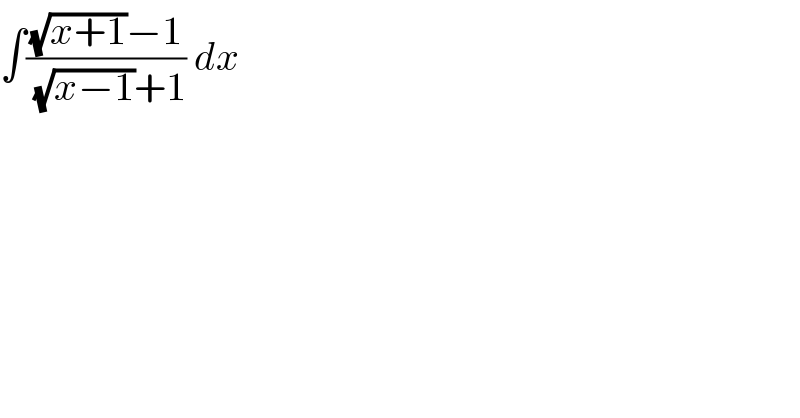
Commented by mathmax by abdo last updated on 23/Mar/20

Answered by MJS last updated on 23/Mar/20
![∫(((√(x+1))−1)/((√(x−1))+1))dx= [t=(√(x−1)) → dx=2(√(x−1))dt] =2∫((t(√(t^2 +2))−t)/(t+1))dt= =−2∫((√(t^2 +2))/(t+1))dt+2∫(√(t^2 +2))dt+2∫(dt/(t+1))−2∫dt −2∫dt=−2t=−2(√(x−1)) • 2∫(dt/(t+1))=2ln (t+1) =2ln ((√(x−1))+1) • 2∫(√(t^2 +2))dt=t(√(t^2 +2))+2ln (t+(√(t^2 +2))) = =(√(x−1))(√(x+1))+2ln ((√(x−1))+(√(x+1))) • −2∫((√(t^2 +2))/(t+1))dt= I prefer t=(√2)sinh (ln u) to avoid another step [u=((t+(√(t^2 +2)))/(√2)) → dt=((√(2(t^2 +2)))/(t+(√t^2 )+2))du=((u^2 +1)/((√2)u^2 ))du] =−(√2)∫(((u^2 +1)^2 )/(u^2 (u^2 +(√2)u−1)))du= =−(√2)∫(((u^2 +1)^2 )/(u^2 (u+(((√2)+(√6))/2))(u+(((√2)−(√6))/2))))du= =2(√3)∫(du/(u+(((√2)+(√6))/2)))−2(√3)∫(du/(u+(((√2)−(√6))/2)))+2∫(du/u)+(√2)∫(du/u^2 )−(√2)∫du= =2(√3)ln (u+(((√2)+(√6))/2)) −2(√3)ln (u+(((√2)−(√6))/2)) +2ln u −((√2)/u)−(√2)u= =2(√3)ln ((2u+(√2)+(√6))/(2u+(√2)−(√6))) +2ln u −(((√2)(u^2 +1))/u)= =2(√3)ln ((2((√(x−1))+(√(x+1)))+(√2)+(√6))/(2((√(x−1))+(√(x+1)))+(√2)−(√6)))+2ln ((√(x−1))+(√(x+1))) −2(√(x+1)) • ⇒ ∫(((√(x+1))−1)/((√(x−1))+1))dx=the sum of the marked terms • please check for typos](Q85626.png)
Commented by M±th+et£s last updated on 23/Mar/20
| ||
Question and Answers Forum | ||
Question Number 85596 by M±th+et£s last updated on 23/Mar/20 | ||
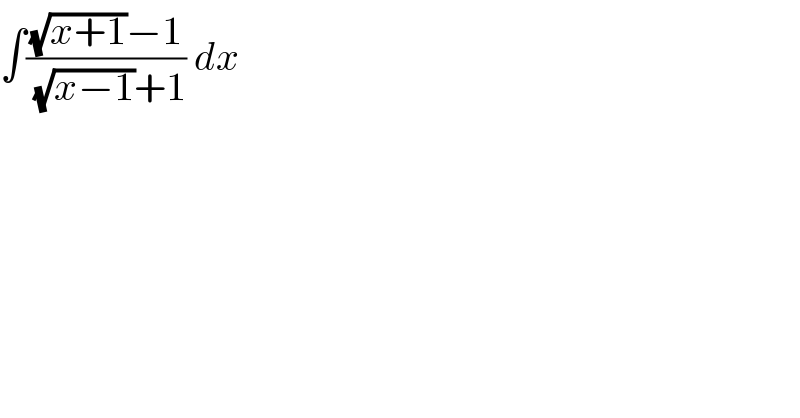 | ||
Commented by mathmax by abdo last updated on 23/Mar/20 | ||
 | ||
Answered by MJS last updated on 23/Mar/20 | ||
![∫(((√(x+1))−1)/((√(x−1))+1))dx= [t=(√(x−1)) → dx=2(√(x−1))dt] =2∫((t(√(t^2 +2))−t)/(t+1))dt= =−2∫((√(t^2 +2))/(t+1))dt+2∫(√(t^2 +2))dt+2∫(dt/(t+1))−2∫dt −2∫dt=−2t=−2(√(x−1)) • 2∫(dt/(t+1))=2ln (t+1) =2ln ((√(x−1))+1) • 2∫(√(t^2 +2))dt=t(√(t^2 +2))+2ln (t+(√(t^2 +2))) = =(√(x−1))(√(x+1))+2ln ((√(x−1))+(√(x+1))) • −2∫((√(t^2 +2))/(t+1))dt= I prefer t=(√2)sinh (ln u) to avoid another step [u=((t+(√(t^2 +2)))/(√2)) → dt=((√(2(t^2 +2)))/(t+(√t^2 )+2))du=((u^2 +1)/((√2)u^2 ))du] =−(√2)∫(((u^2 +1)^2 )/(u^2 (u^2 +(√2)u−1)))du= =−(√2)∫(((u^2 +1)^2 )/(u^2 (u+(((√2)+(√6))/2))(u+(((√2)−(√6))/2))))du= =2(√3)∫(du/(u+(((√2)+(√6))/2)))−2(√3)∫(du/(u+(((√2)−(√6))/2)))+2∫(du/u)+(√2)∫(du/u^2 )−(√2)∫du= =2(√3)ln (u+(((√2)+(√6))/2)) −2(√3)ln (u+(((√2)−(√6))/2)) +2ln u −((√2)/u)−(√2)u= =2(√3)ln ((2u+(√2)+(√6))/(2u+(√2)−(√6))) +2ln u −(((√2)(u^2 +1))/u)= =2(√3)ln ((2((√(x−1))+(√(x+1)))+(√2)+(√6))/(2((√(x−1))+(√(x+1)))+(√2)−(√6)))+2ln ((√(x−1))+(√(x+1))) −2(√(x+1)) • ⇒ ∫(((√(x+1))−1)/((√(x−1))+1))dx=the sum of the marked terms • please check for typos](Q85626.png) | ||
| ||
Commented by M±th+et£s last updated on 23/Mar/20 | ||
 | ||