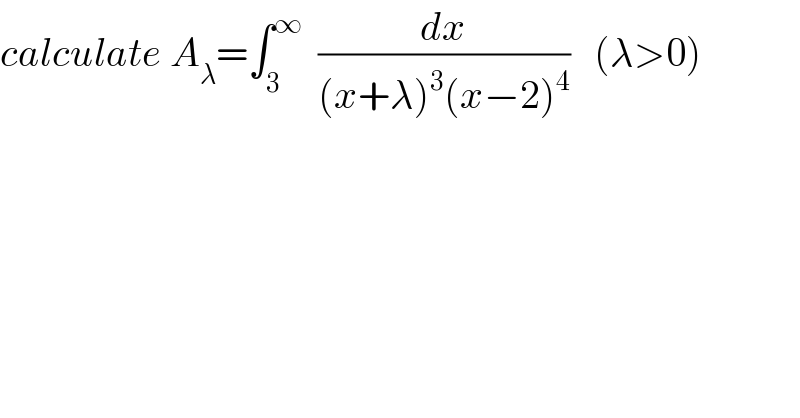
calculate A_λ =∫_3 ^∞ (dx/((x+λ)^3 (x−2)^4 )) (λ>0)


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 85641 by abdomathmax last updated on 23/Mar/20

$c a l c u l a t e A_{λ} = \int_{3}^{\infty} \frac{d x}{{(x + λ)}^{3} {(x - 2)}^{4}} (λ > 0)$
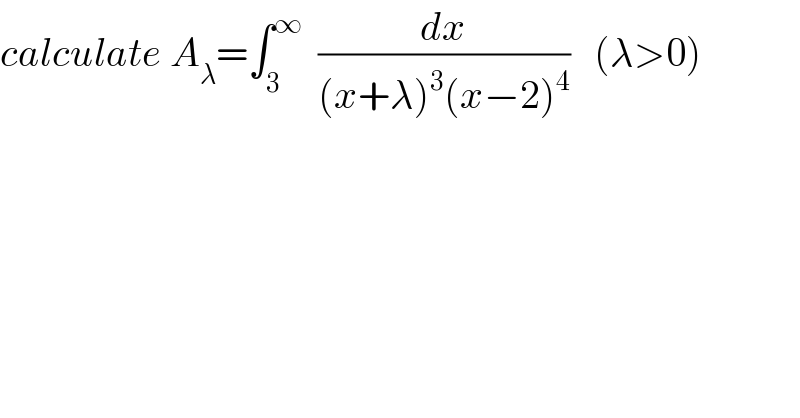Commented bymathmax by abdo last updated on 24/Mar/20
$A_λ =∫_3 ^(+∞) (dx/((((x+λ)/(x−2)))^3 (x−2)^7 )) changement ((x+λ)/(x−2))=t give x+λ =tx−2t ⇒(1−t)x=−2t−λ ⇒x=((−2t−λ)/(1−t)) =((2t+λ)/(t−1)) ⇒ (dx/dt) =((2(t−1)−(2t+λ))/((t−1)^2 )) =((2t−2−2t−λ)/((t−1)^2 )) =((−2−λ)/((t−1)^2 )) x−2 =((2t+λ)/(t−1))−2 =((2t+λ−2t+2)/(t−1)) =((λ+2)/(t−1)) ⇒ A_λ =− ∫_(3+λ) ^1 (1/(t^3 (((λ+2)/(t−1)))^7 ))×((λ+2)/((t−1)^2 ))dt =(1/((λ+2)^6 ))∫_1 ^(3+λ) (dt/(t^3 (((λ+2)/(t−1)))^(−5) )) =(1/((λ+2)))∫_1 ^(3+λ) (((t−1)^5 )/t^3 )dt ⇒ (λ+2)A_λ =∫_1 ^(3+λ) ((Σ_(k=0) ^5 C_5 ^k t^k (−1)^(5−k) )/t^3 )dt =−∫_1 ^(3+λ) Σ_(k=0) ^5 (−1)^k C_5 ^k t^(k−3) dt =−Σ_(k=0) ^5 (−1)^k C_5 ^k ∫_1 ^(3+λ) t^(k−3) dt =−Σ_(k=0 and k≠2) ^5 (−1)^k C_5 ^k [(1/(k−2))t^(k−2) ]_1 ^(3+λ) −C_5 ^2 ∫_1 ^(3+λ) (dt/t) =−Σ_(k=0) ^5 (((−1)^k C_5 ^k )/(k−2)){ (3+λ)^(k−2) −1}−C_5 ^2 {ln∣3+λ∣} ⇒ A_λ =−(1/(λ+2))Σ_(k=0and k≠2) ^5 (((−1)^k C_5 ^k )/(k−2)){(3+λ)^(k−2) −1} −(1/(λ+2)) C_5 ^2 ln∣3+λ∣ .$
$A_{λ} = \int_{3}^{+ \infty} \frac{d x}{{(\frac{x + λ}{x - 2})}^{3} {(x - 2)}^{7}} c h a n g e m e n t \frac{x + λ}{x - 2} = t g i v e$ $x + λ = t x - 2 t \Rightarrow (1 - t) x = - 2 t - λ \Rightarrow x = \frac{- 2 t - λ}{1 - t} = \frac{2 t + λ}{t - 1} \Rightarrow$ $\frac{d x}{d t} = \frac{2 (t - 1) - (2 t + λ)}{{(t - 1)}^{2}} = \frac{2 t - 2 - 2 t - λ}{{(t - 1)}^{2}} = \frac{- 2 - λ}{{(t - 1)}^{2}}$ $x - 2 = \frac{2 t + λ}{t - 1} - 2 = \frac{2 t + λ - 2 t + 2}{t - 1} = \frac{λ + 2}{t - 1} \Rightarrow$ $A_{λ} = - \int_{3 + λ}^{1} \frac{1}{t^{3} {(\frac{λ + 2}{t - 1})}^{7}} \times \frac{λ + 2}{{(t - 1)}^{2}} d t$ $= \frac{1}{{(λ + 2)}^{6}} \int_{1}^{3 + λ} \frac{d t}{t^{3} {(\frac{λ + 2}{t - 1})}^{- 5}} = \frac{1}{(λ + 2)} \int_{1}^{3 + λ} \frac{{(t - 1)}^{5}}{t^{3}} d t \Rightarrow$ $(λ + 2) A_{λ} = \int_{1}^{3 + λ} \frac{\sum_{k = 0}^{5} C_{5}^{k} t^{k} {(- 1)}^{5 - k}}{t^{3}} d t$ $= - \int_{1}^{3 + λ} \sum_{k = 0}^{5} {(- 1)}^{k} C_{5}^{k} t^{k - 3} d t$ $= - \sum_{k = 0}^{5} {(- 1)}^{k} C_{5}^{k} \int_{1}^{3 + λ} t^{k - 3} d t$ $= - \sum_{k = 0 a n d k \neq 2}^{5} {(- 1)}^{k} C_{5}^{k} {[\frac{1}{k - 2} t^{k - 2}]}_{1}^{3 + λ} - C_{5}^{2} \int_{1}^{3 + λ} \frac{d t}{t}$ $= - \sum_{k = 0}^{5} \frac{{(- 1)}^{k} C_{5}^{k}}{k - 2} {{(3 + λ)}^{k - 2} - 1} - C_{5}^{2} {l n ∣ 3 + λ ∣} \Rightarrow$ $A_{λ} = - \frac{1}{λ + 2} \sum_{k = 0 a n d k \neq 2}^{5} \frac{{(- 1)}^{k} C_{5}^{k}}{k - 2} {{(3 + λ)}^{k - 2} - 1}$ $- \frac{1}{λ + 2} C_{5}^{2} l n ∣ 3 + λ ∣ .$
Commented bymathmax by abdo last updated on 24/Mar/20

$λ \neq - 2$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum