
Question Number 85676 by john santu last updated on 24/Mar/20
![∫ _0 ^∞ (dx/((x+(√(1+x^2 )))^2 )) let x = tan t ⇒dx=sec^2 t dt ∫_0 ^(π/2) ((sec^2 t dt)/((tan t+sec t)^2 )) = ∫_0 ^(π/2) (dt/((sin t+1)^2 )) = ∫_0 ^(π/2) (dt/((cos (1/2)t+sin (1/2)t)^4 )) = ∫_0 ^(π/2) (dt/(4cos^4 ((1/2)t−(π/4)))) = (1/4)∫_0 ^(π/2) sec^4 ((1/2)t−(π/4)) dt [ let (1/2)t−(π/4)= u] = (1/4)∫_(−(π/4)) ^0 sec^4 u ×2du =(1/2)∫ _(−(π/4)) ^0 (tan^2 u+1) d(tan u) = (1/2) [(1/3)tan^3 u + tan u ]_(−(π/4)) ^0 = (1/2) [ 0−(−(1/3)−1)]= (2/3)](Q85676.png)
$$\int\underset{\mathrm{0}} {\overset{\infty} {\:}}\:\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$${let}\:{x}\:=\:\mathrm{tan}\:{t}\:\Rightarrow{dx}=\mathrm{sec}\:^{\mathrm{2}} {t}\:{dt} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} {t}\:{dt}}{\left(\mathrm{tan}\:{t}+\mathrm{sec}\:{t}\right)^{\mathrm{2}} }\:=\: \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{dt}}{\left(\mathrm{sin}\:{t}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{dt}}{\left(\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{t}+\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{t}\right)^{\mathrm{4}} } \\ $$$$=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{dt}}{\mathrm{4cos}^{\mathrm{4}} \:\left(\frac{\mathrm{1}}{\mathrm{2}}{t}−\frac{\pi}{\mathrm{4}}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\mathrm{sec}\:^{\mathrm{4}} \left(\frac{\mathrm{1}}{\mathrm{2}}{t}−\frac{\pi}{\mathrm{4}}\right)\:{dt} \\ $$$$\left[\:{let}\:\frac{\mathrm{1}}{\mathrm{2}}{t}−\frac{\pi}{\mathrm{4}}=\:{u}\right] \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\underset{−\frac{\pi}{\mathrm{4}}} {\overset{\mathrm{0}} {\int}}\:\mathrm{sec}\:^{\mathrm{4}} {u}\:×\mathrm{2}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\underset{−\frac{\pi}{\mathrm{4}}} {\overset{\mathrm{0}} {\:}}\left(\mathrm{tan}\:^{\mathrm{2}} {u}+\mathrm{1}\right)\:{d}\left(\mathrm{tan}\:{u}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}\:^{\mathrm{3}} {u}\:+\:\mathrm{tan}\:{u}\:\right]_{−\frac{\pi}{\mathrm{4}}} ^{\mathrm{0}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\mathrm{0}−\left(−\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right)\right]=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$
Commented by jagoll last updated on 24/Mar/20
![i try by Euler substitution let (√(1+x^2 )) = x+t 1+x^2 = x^2 +2xt+t^2 2xt+t^2 =1 ⇒ x = ((1−t^2 )/(2t)) dx = ((−t^2 −1)/(2t^2 )) dt ∫ (1/((((1−t^2 )/(2t))+((1+t^2 )/(2t)))^2 )) × (((−t^2 −1)/(2t^2 ))) dt ∫ (t^2 /(2t^2 )) ×(−t^2 −1) dt = −(1/2)∫ (t^2 +1)dt −(1/2) [(1/3)t^3 +t ] =−(1/6)t [t^2 +3 ] −(1/6) ((√(1+x^2 )) −x ) (2x^2 +4−2x(√(1+x^2 )) ) lim_(x→∞) −(1/6)((√(1+x^2 ))−x)(2x^2 +4−2x(√(1+x^2 ))) +(4/6) = (2/3)](Q85680.png)
$$\mathrm{i}\:\mathrm{try}\:\mathrm{by}\:\:\mathrm{Euler}\:\mathrm{substitution} \\ $$$$\mathrm{let}\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{x}+\mathrm{t}\: \\ $$$$\mathrm{1}+\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{x}^{\mathrm{2}} +\mathrm{2xt}+\mathrm{t}^{\mathrm{2}} \\ $$$$\mathrm{2xt}+\mathrm{t}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow\:\mathrm{x}\:=\:\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{2t}} \\ $$$$\mathrm{dx}\:=\:\frac{−\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }\:\mathrm{dt} \\ $$$$\int\:\frac{\mathrm{1}}{\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{2t}}+\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{2t}}\right)^{\mathrm{2}} }\:×\:\left(\frac{−\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }\right)\:\mathrm{dt} \\ $$$$\int\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2t}^{\mathrm{2}} }\:×\left(−\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\:\mathrm{dt}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{dt} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\:\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\mathrm{3}} +\mathrm{t}\:\right]\:=−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{t}\:\left[\mathrm{t}^{\mathrm{2}} +\mathrm{3}\:\right] \\ $$$$−\frac{\mathrm{1}}{\mathrm{6}}\:\left(\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:−\mathrm{x}\:\right)\:\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{4}−\mathrm{2x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:−\frac{\mathrm{1}}{\mathrm{6}}\left(\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\mathrm{x}\right)\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{4}−\mathrm{2x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:+\frac{\mathrm{4}}{\mathrm{6}} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 24/Mar/20

$${good} \\ $$
Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20
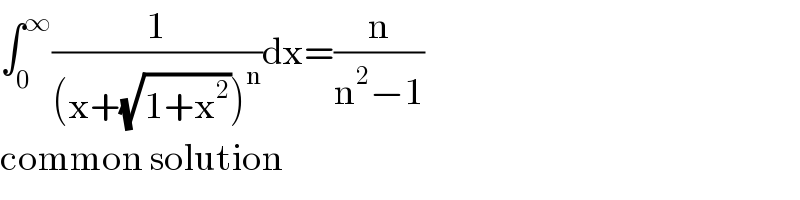
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{n}} }\mathrm{dx}=\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{common}\:\mathrm{solution} \\ $$
Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20

$$\mathrm{comment}\:\mathrm{pls} \\ $$
Commented by john santu last updated on 24/Mar/20
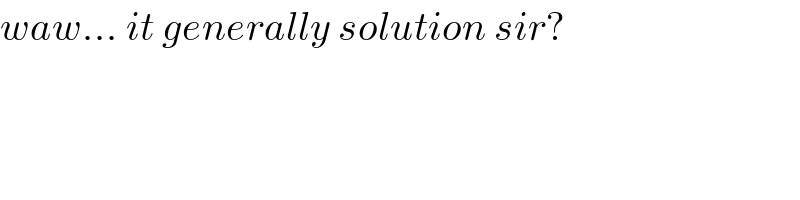
$${waw}...\:{it}\:{generally}\:{solution}\:{sir}? \\ $$
Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20
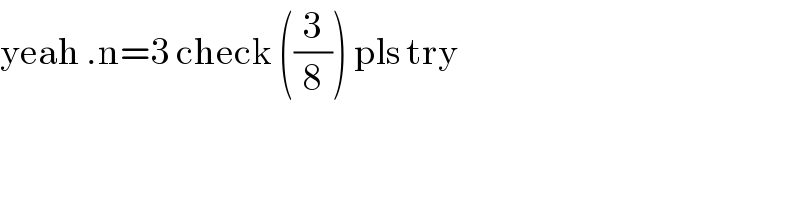
$$\mathrm{yeah}\:.\mathrm{n}=\mathrm{3}\:\mathrm{check}\:\left(\frac{\mathrm{3}}{\mathrm{8}}\right)\:\mathrm{pls}\:\mathrm{try} \\ $$
Commented by jagoll last updated on 24/Mar/20

$$\mathrm{but}\:\mathrm{n}\:\neq\:\mathrm{1}? \\ $$
Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20
![sry (n/((n^2 −1))) ,[n^2 −1≠0] so (n≠1) & (n≠−1)](Q85726.png)
$$\mathrm{sry}\:\frac{\mathrm{n}}{\left(\mathrm{n}^{\mathrm{2}} −\mathrm{1}\right)}\:\:,\left[\mathrm{n}^{\mathrm{2}} −\mathrm{1}\neq\mathrm{0}\right]\:\mathrm{so}\:\:\left(\mathrm{n}\neq\mathrm{1}\right)\:\&\:\left(\mathrm{n}\neq−\mathrm{1}\right) \\ $$
Commented by sakeefhasan05@gmail.com last updated on 24/Mar/20
$$\mathrm{thank}\:\mathrm{you}\:\:\mathrm{for}\:\mathrm{direct}\:\mathrm{me} \\ $$
Commented by mathmax by abdo last updated on 24/Mar/20
![let A_n =∫_0 ^∞ (dx/((x+(√(1+x^2 )))^n )) we do the changement x=sh(t) ⇒ A_n =∫_0 ^∞ ((ch(t))/((sh(t)+ch(t))^n ))dt =∫_0 ^∞ ((ch(t))/((((e^t −e^(−t) )/2)+((e^t +e^(−t) )/2))^n ))dt =∫_0 ^∞ e^(−nt) (((e^t +e^(−t) )/2))dt =(1/2) ∫_0 ^∞ ( e^((−n+1)t) +e^(−(n+1)t) )dt =(1/2)[(1/(1−n))e^((1−n)t) −(1/(n+1))e^(−(n+1)t) ]_0 ^(+∞) =(1/2){−(1/(1−n))+(1/(n+1))} =(1/2)((1/(n+1))+(1/(n−1))) =(1/2)(((2n)/(n^2 −1))) ⇒ A_n =(n/(n^2 −1)) (n>1) so ∫_0 ^∞ (dx/((x+(√(1+x^2 )))^2 )) =(2/(2^2 −1)) =(2/3)](Q85731.png)
$${let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{{n}} }\:\:{we}\:{do}\:{the}\:{changement}\:{x}={sh}\left({t}\right)\:\Rightarrow \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ch}\left({t}\right)}{\left({sh}\left({t}\right)+{ch}\left({t}\right)\right)^{{n}} }{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ch}\left({t}\right)}{\left(\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}+\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}\right)^{{n}} }{dt}\:\: \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{nt}} \left(\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\left(\:{e}^{\left(−{n}+\mathrm{1}\right){t}} \:+{e}^{−\left({n}+\mathrm{1}\right){t}} \right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{1}−{n}}{e}^{\left(\mathrm{1}−{n}\right){t}} \:−\frac{\mathrm{1}}{{n}+\mathrm{1}}{e}^{−\left({n}+\mathrm{1}\right){t}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\frac{\mathrm{1}}{\mathrm{1}−{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}\right\}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}−\mathrm{1}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}{n}}{{n}^{\mathrm{2}} −\mathrm{1}}\right)\:\Rightarrow \\ $$$${A}_{{n}} =\frac{{n}}{{n}^{\mathrm{2}} −\mathrm{1}}\:\:\:\left({n}>\mathrm{1}\right)\:\:{so} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 24/Mar/20
$${thank}\:{you}\:{sir}\:{for}\:{your}\:{short}\:{cut} \\ $$
Commented by john santu last updated on 24/Mar/20

$${indonesian}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 24/Mar/20
$${where}\:{are}\:{you}\:{from}\:{sir}\:{john}... \\ $$
Commented by mathmax by abdo last updated on 24/Mar/20

$${aah}\:{good}\:\:{sir}\:... \\ $$
Commented by john santu last updated on 25/Mar/20

$${why}\:{sir}?\:{if}\:{you}\:{where}\:{you}\: \\ $$$${come}\:{sir}? \\ $$
