Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 85701 by jagoll last updated on 24/Mar/20

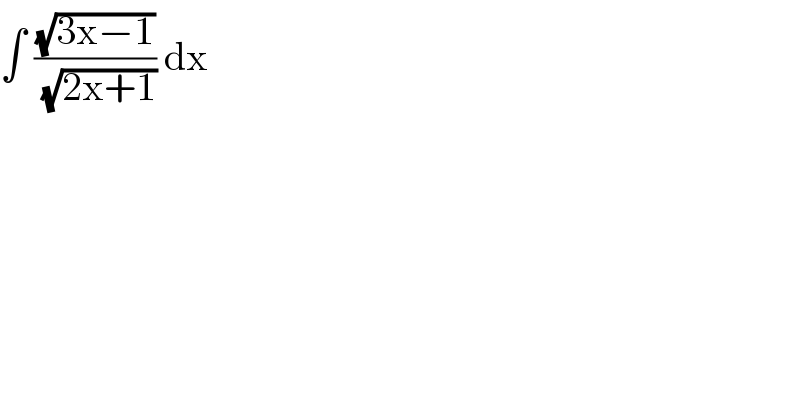
∫ ((√(3x−1))/(√(2x+1))) dx

$$\int\:\frac{\sqrt{\mathrm{3x}−\mathrm{1}}}{\sqrt{\mathrm{2x}+\mathrm{1}}}\:\mathrm{dx}\: \\ $$

Commented by john santu last updated on 24/Mar/20

let t = (√(2x+1)) ⇒ x = ((t^2 −1)/2) ∫ ((√(((3t^2 −3)/2)−1))/t)×t dt = ∫ (√((3t^2 −5)/2)) dt = (1/((√2) ))∫ (√(3t^2 −5)) dt = [ (√3) t=(√5) sec u ] (1/((√2) ))∫ (√(5tan^2 u)) ×((√5)/(√3)) sec u tan u du = (5/(√6)) ∫ tan^2 u sec u du = (5/((√6) ))[∫sec^3 u du−ln ∣sec u+tan u∣ +c (5/(2(√6))) sec utan u−(5/(2(√6))) ln∣sec u+tan u∣+c (5/(2(√6) )).((√3)/(√5)) t ((√(3t^2 −5))/(√5)) −(5/(2(√6))) ln ∣(((√3) t+(√(3t^2 −5)))/(√5))∣ +c (1/(2(√2))) (√(2x+1)) (√(6x−2)) −(5/(2(√6))) ln ∣(((√(6x+3))+(√(6x−2)))/(√5))∣ +c

$${let}\:{t}\:=\:\sqrt{\mathrm{2}{x}+\mathrm{1}}\:\Rightarrow\:{x}\:=\:\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\int\:\frac{\sqrt{\frac{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{3}}{\mathrm{2}}−\mathrm{1}}}{{t}}×{t}\:{dt}\:=\: \\ $$$$\int\:\sqrt{\frac{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{5}}{\mathrm{2}}}\:{dt}\:=\: \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:}\int\:\sqrt{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{5}}\:{dt}\:= \\ $$$$\left[\:\sqrt{\mathrm{3}}\:{t}=\sqrt{\mathrm{5}}\:\mathrm{sec}\:{u}\:\right] \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:}\int\:\sqrt{\mathrm{5tan}\:^{\mathrm{2}} {u}}\:×\frac{\sqrt{\mathrm{5}}}{\sqrt{\mathrm{3}}}\:\mathrm{sec}\:{u}\:\mathrm{tan}\:{u}\:{du}\:= \\ $$$$\frac{\mathrm{5}}{\sqrt{\mathrm{6}}}\:\int\:\mathrm{tan}\:^{\mathrm{2}} {u}\:\mathrm{sec}\:{u}\:{du}\:= \\ $$$$\frac{\mathrm{5}}{\sqrt{\mathrm{6}}\:}\left[\int\mathrm{sec}\:^{\mathrm{3}} {u}\:{du}−\mathrm{ln}\:\mid\mathrm{sec}\:{u}+\mathrm{tan}\:{u}\mid\:+{c}\:\right. \\ $$$$\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{6}}}\:\mathrm{sec}\:{u}\mathrm{tan}\:{u}−\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{6}}}\:\mathrm{ln}\mid\mathrm{sec}\:{u}+\mathrm{tan}\:{u}\mid+{c} \\ $$$$\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{6}}\:}.\frac{\sqrt{\mathrm{3}}}{\sqrt{\mathrm{5}}}\:{t}\:\frac{\sqrt{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{5}}}{\sqrt{\mathrm{5}}}\:−\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{6}}}\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{3}}\:{t}+\sqrt{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{5}}}{\sqrt{\mathrm{5}}}\mid\:+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\sqrt{\mathrm{2}{x}+\mathrm{1}}\:\sqrt{\mathrm{6}{x}−\mathrm{2}}\:−\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{6}}}\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{6}{x}+\mathrm{3}}+\sqrt{\mathrm{6}{x}−\mathrm{2}}}{\sqrt{\mathrm{5}}}\mid\:+{c} \\ $$

Commented by mathmax by abdo last updated on 24/Mar/20

I =∫(√((3x−1)/(2x+1)))dx changement (√((3x−1)/(2x+1)))=t give ((3x−1)/(2x+1)) =t^2 ⇒3x−1 =2t^2 x+t^2 ⇒(3−2t^2 )x =t^2 +1 ⇒ x=((t^(2 ) +1)/(3−2t^2 )) ⇒dx =((2t(3−2t^2 )−(t^2 +1)(−4t))/((3−2t^2 )^2 ))dt =((6t−4t^3 +4t^3 +4t)/((2t^2 −3)^2 ))dt =((10t)/((2t^2 −3)^2 ))dt ⇒I =∫t×((10t)/((2t^2 −3)^2 ))dt =5 ∫ ((2t^2 −3+3)/((2t^2 −3)^2 ))dt =5 ∫ (dt/(2t^2 −3)) +15 ∫ (dt/((2t^2 −3)^2 )) we have ∫ (dt/(2t^2 −3)) =(1/2)∫ (dt/(t^2 −((√(3/2)))^2 )) =(1/(2×2(√(3/2))))∫((1/(t−(√(3/2))))−(1/(t+(√(3/2))))) =((√2)/(4(√3)))ln∣((t−(√(3/2)))/(t+(√(3/2))))∣ +c_0 ∫ (dt/((2t^2 −3)^2 )) =(1/4)∫ (dt/((t−(√(3/2)))^2 (t+(√(3/2)))^2 )) =(a/(t−(√(3/2)))) +(b/((t−(√(3/2)))^2 )) +(c/(t+(√(3/2)))) +(d/((t+(√(3/2)))^2 ))=F(t) ⇒∫ F(t)dt =aln∣t−(√(3/2))∣−(b/(t−(√(3/2)))) +cln∣t+(√(3/2))∣−(d/(t+(√(3/2)))) with t=(√((3x−1)/(2x+1))) rest calculus of coefficient ...be continued...

$${I}\:=\int\sqrt{\frac{\mathrm{3}{x}−\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}}{dx}\:\:{changement}\:\sqrt{\frac{\mathrm{3}{x}−\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}}={t}\:{give} \\ $$$$\frac{\mathrm{3}{x}−\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}\:={t}^{\mathrm{2}} \:\Rightarrow\mathrm{3}{x}−\mathrm{1}\:=\mathrm{2}{t}^{\mathrm{2}} {x}+{t}^{\mathrm{2}} \:\Rightarrow\left(\mathrm{3}−\mathrm{2}{t}^{\mathrm{2}} \right){x}\:={t}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow \\ $$$${x}=\frac{{t}^{\mathrm{2}\:} +\mathrm{1}}{\mathrm{3}−\mathrm{2}{t}^{\mathrm{2}} }\:\Rightarrow{dx}\:=\frac{\mathrm{2}{t}\left(\mathrm{3}−\mathrm{2}{t}^{\mathrm{2}} \right)−\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left(−\mathrm{4}{t}\right)}{\left(\mathrm{3}−\mathrm{2}{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{6}{t}−\mathrm{4}{t}^{\mathrm{3}} +\mathrm{4}{t}^{\mathrm{3}} +\mathrm{4}{t}}{\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} }{dt}\:=\frac{\mathrm{10}{t}}{\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} }{dt}\:\Rightarrow{I}\:=\int{t}×\frac{\mathrm{10}{t}}{\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{5}\:\int\:\:\:\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}+\mathrm{3}}{\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} }{dt}\:=\mathrm{5}\:\int\:\:\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}}\:+\mathrm{15}\:\int\:\:\frac{{dt}}{\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} }\:\:{we}\:{have} \\ $$$$\int\:\:\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\left(\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}×\mathrm{2}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}}\int\left(\frac{\mathrm{1}}{{t}−\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}}−\frac{\mathrm{1}}{{t}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}}\right) \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}\sqrt{\mathrm{3}}}{ln}\mid\frac{{t}−\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}}{{t}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}}\mid\:+{c}_{\mathrm{0}} \\ $$$$\int\:\:\:\frac{{dt}}{\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\frac{{dt}}{\left({t}−\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{2}} \left({t}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{2}} } \\ $$$$=\frac{{a}}{{t}−\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}}\:+\frac{{b}}{\left({t}−\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{2}} }\:+\frac{{c}}{{t}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}}\:+\frac{{d}}{\left({t}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{2}} }={F}\left({t}\right) \\ $$$$\Rightarrow\int\:{F}\left({t}\right){dt}\:={aln}\mid{t}−\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\mid−\frac{{b}}{{t}−\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}}\:+{cln}\mid{t}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\mid−\frac{{d}}{{t}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}} \\ $$$${with}\:{t}=\sqrt{\frac{\mathrm{3}{x}−\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}}\:{rest}\:{calculus}\:{of}\:{coefficient}\:...{be}\:{continued}... \\ $$

Commented by john santu last updated on 24/Mar/20

wrong? where?

$${wrong}?\:{where}? \\ $$

Answered by MJS last updated on 24/Mar/20

∫((√(3x−1))/(√(2x+1)))dx= [t=((√(2x+1))/(√(3x−1))) → dx=−(2/5)(√(2x+1))(√((3x−1)^3 ))dt] =−((10)/9)∫(dt/((t^2 −(2/3))^2 ))= [Ostrogradski′s Method] =((5t)/(6(t^2 −(2/3))))+(5/6)∫(dt/(t^2 −(2/3)))= =((5t)/(6(t^2 −(2/3))))+((5(√6))/(24))ln ((3t−(√6))/(3t+(√6))) = =(1/2)(√(3x−1))(√(2x+1))+((5(√6))/(24))ln (6x+(1/2)−(√(3x−1))(√(2x+1))) +C

$$\int\frac{\sqrt{\mathrm{3}{x}−\mathrm{1}}}{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{2}{x}+\mathrm{1}}}{\sqrt{\mathrm{3}{x}−\mathrm{1}}}\:\rightarrow\:{dx}=−\frac{\mathrm{2}}{\mathrm{5}}\sqrt{\mathrm{2}{x}+\mathrm{1}}\sqrt{\left(\mathrm{3}{x}−\mathrm{1}\right)^{\mathrm{3}} }{dt}\right] \\ $$$$=−\frac{\mathrm{10}}{\mathrm{9}}\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{\mathrm{5}{t}}{\mathrm{6}\left({t}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}\right)}+\frac{\mathrm{5}}{\mathrm{6}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}}= \\ $$$$=\frac{\mathrm{5}{t}}{\mathrm{6}\left({t}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}\right)}+\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{24}}\mathrm{ln}\:\frac{\mathrm{3}{t}−\sqrt{\mathrm{6}}}{\mathrm{3}{t}+\sqrt{\mathrm{6}}}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}{x}−\mathrm{1}}\sqrt{\mathrm{2}{x}+\mathrm{1}}+\frac{\mathrm{5}\sqrt{\mathrm{6}}}{\mathrm{24}}\mathrm{ln}\:\left(\mathrm{6}{x}+\frac{\mathrm{1}}{\mathrm{2}}−\sqrt{\mathrm{3}{x}−\mathrm{1}}\sqrt{\mathrm{2}{x}+\mathrm{1}}\right)\:+{C} \\ $$

Commented by MJS last updated on 24/Mar/20

sorry your solution is ok, I made a mistake while going through it.

$$\mathrm{sorry}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{ok},\:\mathrm{I}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake} \\ $$$$\mathrm{while}\:\mathrm{going}\:\mathrm{through}\:\mathrm{it}. \\ $$

Commented by john santu last updated on 24/Mar/20

the results of an integral can be different from one another because of different method . but they are true as a solution

$${the}\:{results}\:{of}\:{an}\:{integral}\: \\ $$$${can}\:{be}\:{different}\:{from}\:{one}\: \\ $$$${another}\:{because}\:{of}\:{different} \\ $$$${method}\:.\:{but}\:{they}\:{are}\:{true}\:{as} \\ $$$${a}\:{solution} \\ $$

Commented by john santu last updated on 24/Mar/20

for example ∫ sin x cos x dx = ∫ sin x d(sin x) = (1/2)sin^2 x + c ∫ sin x cos x dx = (1/2)∫ sin 2x dx = −(1/4) cos 2x + c

$${for}\:{example}\: \\ $$$$\int\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:{dx}\:=\:\int\:\mathrm{sin}\:{x}\:{d}\left(\mathrm{sin}\:{x}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} {x}\:+\:{c} \\ $$$$\int\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{sin}\:\mathrm{2}{x}\:{dx} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{cos}\:\mathrm{2}{x}\:+\:{c} \\ $$

Commented by john santu last updated on 24/Mar/20

thank you mister

$${thank}\:{you}\:{mister} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com