
Question and Answers Forum
Question Number 85718 by M±th+et£s last updated on 24/Mar/20
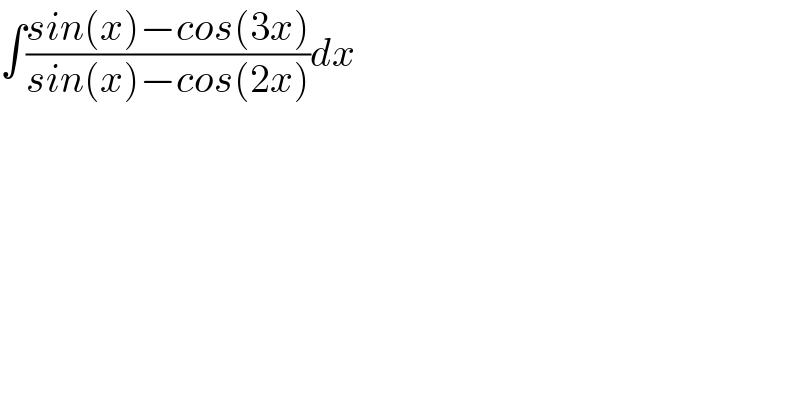
Answered by MJS last updated on 24/Mar/20
![∫((sin x −cos 3x)/(sin x −cos 2x))dx= =∫((4cos x sin^2 x −cos x +sin x)/(−2cos^2 x +sin x +1))dx= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−2∫((t^6 +2t^5 −15t^4 +4t^3 +15t^2 +2t−1)/(t^8 −2t^7 −4t^6 −6t^5 −10t^4 −6t^3 −4t^2 −2t+1))dt= =−2∫((...)/((t^2 +1)^2 (t+1)^2 (t−2−(√3))(t−2+(√3))))dt= =8∫(dt/((t^2 +1)^2 ))+∫((2t)/(t^2 +1))dt−4∫(dt/(t^2 +1))+(2/3)∫(dt/((t^2 +1)^2 ))−2∫(dt/(t+1))−((√3)/9)∫(dt/(t−2−(√3)))+((√3)/9)∫(dt/(t−2+(√3))) now it′s easy](Q85754.png)
Commented by MJS last updated on 24/Mar/20
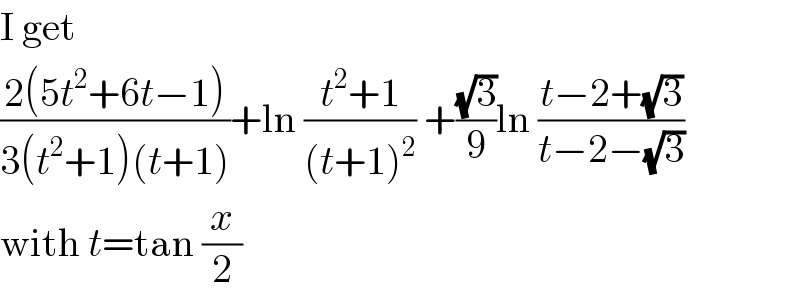
Commented by M±th+et£s last updated on 24/Mar/20

| ||
Question and Answers Forum | ||
Question Number 85718 by M±th+et£s last updated on 24/Mar/20 | ||
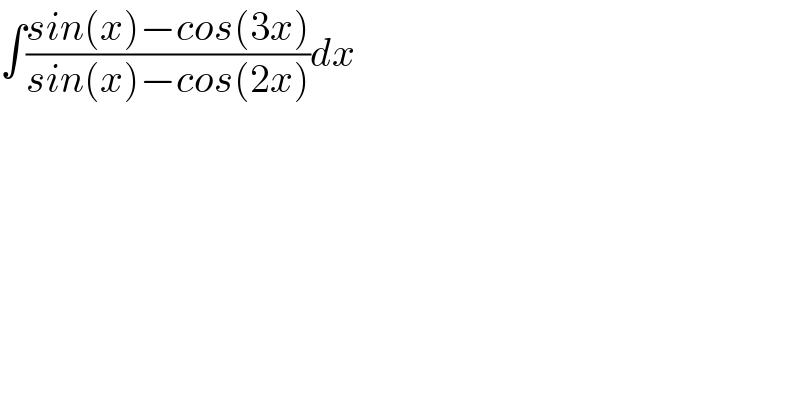 | ||
Answered by MJS last updated on 24/Mar/20 | ||
![∫((sin x −cos 3x)/(sin x −cos 2x))dx= =∫((4cos x sin^2 x −cos x +sin x)/(−2cos^2 x +sin x +1))dx= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−2∫((t^6 +2t^5 −15t^4 +4t^3 +15t^2 +2t−1)/(t^8 −2t^7 −4t^6 −6t^5 −10t^4 −6t^3 −4t^2 −2t+1))dt= =−2∫((...)/((t^2 +1)^2 (t+1)^2 (t−2−(√3))(t−2+(√3))))dt= =8∫(dt/((t^2 +1)^2 ))+∫((2t)/(t^2 +1))dt−4∫(dt/(t^2 +1))+(2/3)∫(dt/((t^2 +1)^2 ))−2∫(dt/(t+1))−((√3)/9)∫(dt/(t−2−(√3)))+((√3)/9)∫(dt/(t−2+(√3))) now it′s easy](Q85754.png) | ||
| ||
Commented by MJS last updated on 24/Mar/20 | ||
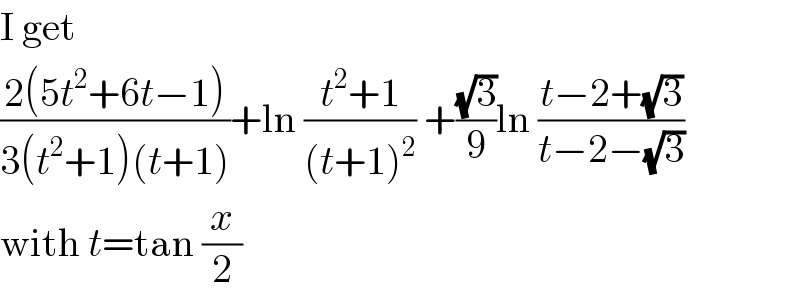 | ||
Commented by M±th+et£s last updated on 24/Mar/20 | ||
 | ||