Question Number 85781 by Joel578 last updated on 24/Mar/20
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{ln}\:\frac{\mathrm{1}}{{x}}\right)^{−\mathrm{3}/\mathrm{2}} \:{dx} \\ $$
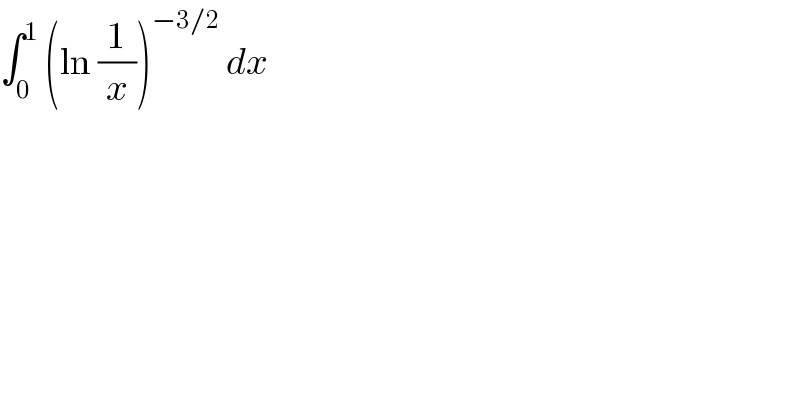
Commented by Joel578 last updated on 24/Mar/20
$$\mathrm{If}\:\mathrm{we}\:\mathrm{use}\:{u}\:=\:\mathrm{ln}\:\frac{\mathrm{1}}{{x}},\:\mathrm{the}\:\mathrm{integral}\:\mathrm{will}\:\mathrm{become} \\ $$$$\int_{\mathrm{0}} ^{\infty} {u}^{−\mathrm{3}/\mathrm{2}} \:{e}^{−{u}} \:{du}\:\:\:\mathrm{which}\:\mathrm{is}\:\Gamma\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:−\mathrm{2}\sqrt{\pi} \\ $$$$\mathrm{But}\:\mathrm{we}\:\mathrm{know}\:\mathrm{for}\:\mathrm{0}<{x}<\mathrm{1},\:\mathrm{the}\:\mathrm{graph}\:\mathrm{of}\: \\ $$$${y}\:=\:\left(\mathrm{ln}\:\frac{\mathrm{1}}{{x}}\right)^{−\mathrm{3}/\mathrm{2}} \:\:\mathrm{is}\:\mathrm{always}\:\mathrm{above}\:{x}−\mathrm{axis},\:\mathrm{so} \\ $$$$\mathrm{the}\:\mathrm{integral}\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{negative}. \\ $$$$\mathrm{I}{s}\:\mathrm{my}\:\mathrm{method}\:\mathrm{invalid}? \\ $$
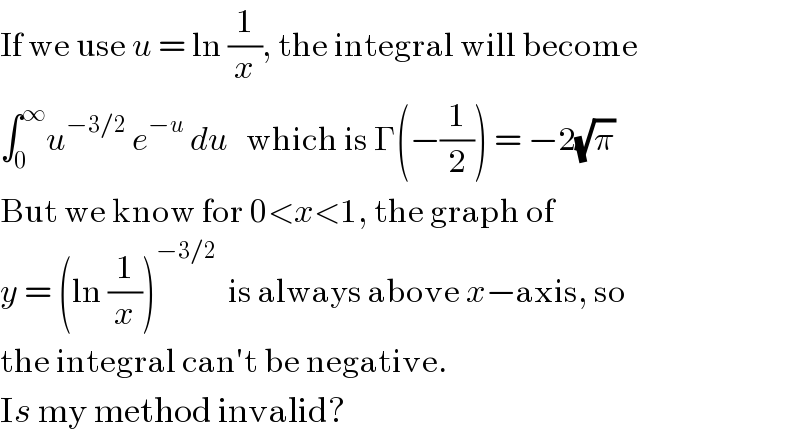
Commented by MJS last updated on 24/Mar/20
$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure},\:\mathrm{but}\:\mathrm{the}\:\mathrm{integral}\:\Gamma\left({x}\right)\:\mathrm{only} \\ $$$$\mathrm{converges}\:\mathrm{for}\:{x}>\mathrm{0}.\:\mathrm{for}\:{x}<\mathrm{0}\wedge{x}\notin\mathbb{Z}\:\mathrm{we}\:\mathrm{must} \\ $$$$\mathrm{calculate}\:\mathrm{backwards}:\:\Gamma\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{−\frac{\mathrm{1}}{\mathrm{2}}}=−\mathrm{2}\sqrt{\pi} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{might}\:\mathrm{be},\:\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to} \\ $$$$\mathrm{integrate}\:\left(\mathrm{ln}\:\frac{\mathrm{1}}{{x}}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{you}\:\mathrm{cannot}\:\mathrm{use}\:\mathrm{the} \\ $$$$\mathrm{gamma}\:\mathrm{function} \\ $$
Answered by MJS last updated on 24/Mar/20
![∫(ln (1/x))^(−3/2) dx= [t=ln (1/x) → dx=−xdt] =−∫e^(−t) t^(−3/2) dt= [by parts: f ′=t^(−3/2) → f=−2t^(−1/2) g=e^(−t) →g′=−e^(−t) ] =2e^(−t) t^(−1/2) +2∫e^(−t) t^(−1/2) dt= [2∫e^(−t) t^(−1/2) dt= [u=(√t) → dt=2(√t)du] =4∫e^(−u^2 ) du=2(√π)∫((2e^(−u^2 ) )/(√π))du=2(√π)erf (u) = =2(√π)erf ((√t))] =2e^(−t) t^(−1/2) +2(√π)erf ((√t)) = =((2x)/(√(ln (1/x))))+2(√π)erf ((√(ln (1/x)))) +C but this integral does not converge for 0≤x≤1...](Q85787.png)
$$\int\left(\mathrm{ln}\:\frac{\mathrm{1}}{{x}}\right)^{−\mathrm{3}/\mathrm{2}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{ln}\:\frac{\mathrm{1}}{{x}}\:\rightarrow\:{dx}=−{xdt}\right] \\ $$$$=−\int\mathrm{e}^{−{t}} {t}^{−\mathrm{3}/\mathrm{2}} {dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}:\:{f}\:'={t}^{−\mathrm{3}/\mathrm{2}} \:\rightarrow\:{f}=−\mathrm{2}{t}^{−\mathrm{1}/\mathrm{2}} \right. \\ $$$$\left.\:\:\:\:\:\:\:{g}=\mathrm{e}^{−{t}} \:\rightarrow{g}'=−\mathrm{e}^{−{t}} \right] \\ $$$$=\mathrm{2e}^{−{t}} {t}^{−\mathrm{1}/\mathrm{2}} +\mathrm{2}\int\mathrm{e}^{−{t}} {t}^{−\mathrm{1}/\mathrm{2}} {dt}= \\ $$$$ \\ $$$$\:\:\:\:\:\left[\mathrm{2}\int\mathrm{e}^{−{t}} {t}^{−\mathrm{1}/\mathrm{2}} {dt}=\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\sqrt{{t}}\:\rightarrow\:{dt}=\mathrm{2}\sqrt{{t}}{du}\right] \\ $$$$\:\:\:\:\:=\mathrm{4}\int\mathrm{e}^{−{u}^{\mathrm{2}} } {du}=\mathrm{2}\sqrt{\pi}\int\frac{\mathrm{2e}^{−{u}^{\mathrm{2}} } }{\sqrt{\pi}}{du}=\mathrm{2}\sqrt{\pi}\mathrm{erf}\:\left({u}\right)\:= \\ $$$$\left.\:\:\:\:\:=\mathrm{2}\sqrt{\pi}\mathrm{erf}\:\left(\sqrt{{t}}\right)\right] \\ $$$$ \\ $$$$=\mathrm{2e}^{−{t}} {t}^{−\mathrm{1}/\mathrm{2}} +\mathrm{2}\sqrt{\pi}\mathrm{erf}\:\left(\sqrt{{t}}\right)\:= \\ $$$$=\frac{\mathrm{2}{x}}{\sqrt{\mathrm{ln}\:\frac{\mathrm{1}}{{x}}}}+\mathrm{2}\sqrt{\pi}\mathrm{erf}\:\left(\sqrt{\mathrm{ln}\:\frac{\mathrm{1}}{{x}}}\right)\:+{C} \\ $$$$\mathrm{but}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge}\:\mathrm{for} \\ $$$$\mathrm{0}\leqslant{x}\leqslant\mathrm{1}... \\ $$
Commented by Joel578 last updated on 25/Mar/20
$${thank}\:{you}\:{very}\:{much} \\ $$