
Question and Answers Forum
Question Number 85902 by mr W last updated on 26/Mar/20
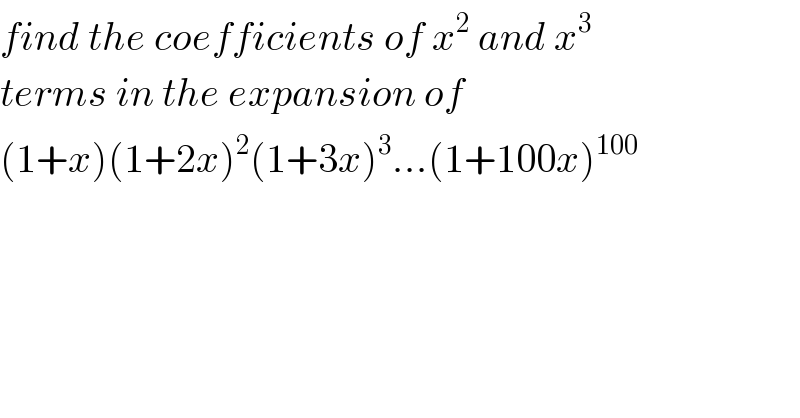
Commented by Serlea last updated on 26/Mar/20

Commented by mr W last updated on 26/Mar/20
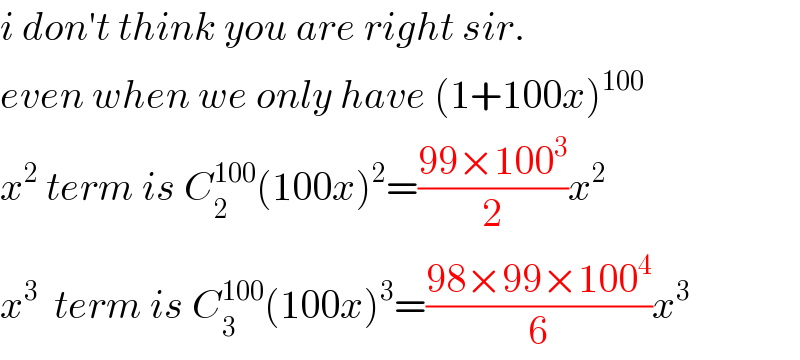
Commented by Serlea last updated on 26/Mar/20
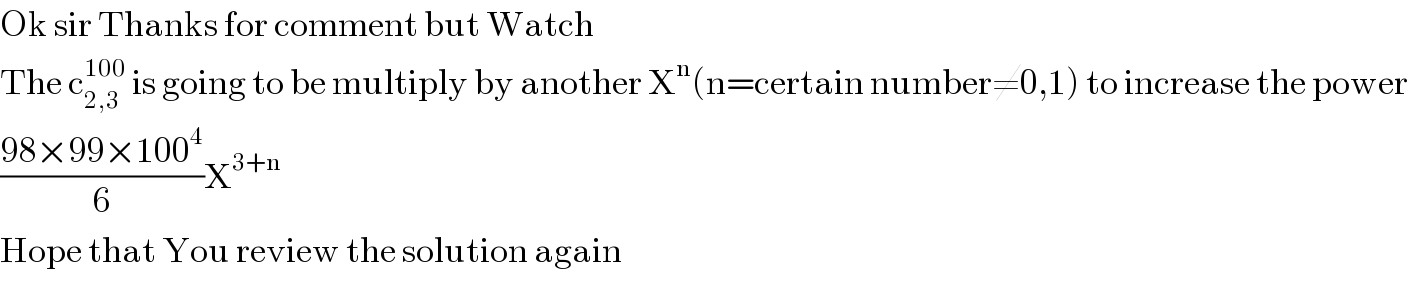
Commented by mr W last updated on 26/Mar/20

Commented by Serlea last updated on 26/Mar/20

Commented by mr W last updated on 26/Mar/20

Commented by Kunal12588 last updated on 26/Mar/20
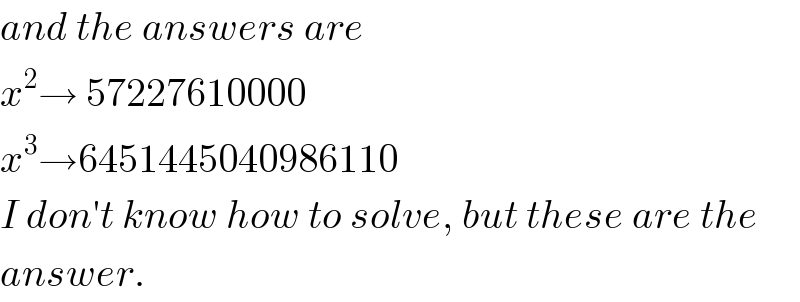
Commented by jagoll last updated on 26/Mar/20
Commented by naka3546 last updated on 26/Mar/20

Commented by jagoll last updated on 26/Mar/20

Commented by naka3546 last updated on 26/Mar/20

Commented by Serlea last updated on 26/Mar/20
Commented by TawaTawa1 last updated on 26/Mar/20

Commented by Prithwish Sen 1 last updated on 26/Mar/20

Commented by Serlea last updated on 26/Mar/20

Answered by mr W last updated on 06/Apr/20
![let n=100 P=(1+x)(1+2x)^2 (1+3x)^3 ...(1+100x)^(100) =P_1 P_2 P_3 ...P_k ...P_n P_k =(1+kx)^k =Σ_(r=0) ^k C_r ^k (kx)^r P_k =1+k(kx)+((k(k−1))/(2!))(kx)^2 +((k(k−1)(k−2))/(3!))(kx)^3 +((k(k−1)(k−2)(k−3))/(4!))(kx)^4 +o(x^4 ) =1+k^2 x+((k^3 (k−1))/2)x^2 +((k^4 (k−1)(k−2))/6)x^3 +((k^5 (k−1)(k−2)(k−3))/(24))x^4 +o(x^4 ) ⇒P_k =1+a_(k,1) x+a_(k,2) x^2 +a_(k,3) x^3 +a_(k,4) x^4 +o(x^4 ) with a_(k^� ,1) =k^2 , a_(k,2) =((k^3 (k−1))/2), a_(k,3) =((k^4 (k−1)(k−2))/6), a_(k,4) =((k^5 (k−1)(k−2)(k−3))/(24)) k=1,2,3,...,n coef. of x term: C_1 =Σ_(k=1) ^n a_(k,1) =Σ_(k=1) ^n k^2 =((n(n+1)(2n+1))/6) with n=100, C_1 =((100×101×201)/6)=338 350 coef. of x^2 term: C_2 =Σ_(k=1) ^n Σ_(j=k+1) ^n a_(k,1) a_(j,1) +Σ_(k=1) ^n a_(k,2) =(1/2)Σ_(k=1) ^n a_(k,1) (Σ_(j=1) ^n a_(j,1) −a_(k,1) )+Σ_(k=1) ^n a_(k,2) =(1/2)[(Σ_(k=1) ^n a_(k,1) )^2 −Σ_(k=1) ^n a_(k,1) ^2 ]+Σ_(k=1) ^n a_(k^� 2) =(1/2)[(Σ_(k=1) ^n k^2 )^2 −Σ_(k=1) ^n k^4 ]+Σ_(k=1) ^n ((k^3 (k−1))/2) =(1/2)(Σ_(k=1) ^n k^2 )^2 −(1/2)Σ_(k=1) ^n k^4 +(1/2)Σ_(k=1) ^n k^4 −(1/2)Σ_(k=1) ^n k^3 =(1/2)(Σ_(k=1) ^n k^2 )^2 −(1/2)Σ_(k=1) ^n k^3 =(1/2)[((n(n+1)(2n+1))/6)]^2 −(1/2)[((n(n+1))/2)]^2 =(((n−1)n^2 (n+1)^2 (n+2))/(18)) with n=100, C_2 =((99×100^2 ×101^2 ×102)/(18))=57 227 610 000 (to be continued)](Q85984.png)
Commented by TawaTawa1 last updated on 26/Mar/20
Commented by TawaTawa1 last updated on 26/Mar/20
Commented by Prithwish Sen 1 last updated on 26/Mar/20

Commented by Prithwish Sen 1 last updated on 26/Mar/20
Commented by Prithwish Sen 1 last updated on 27/Mar/20
Commented by Prithwish Sen 1 last updated on 26/Mar/20

Commented by mr W last updated on 05/Apr/20
![(continued) let K_2 =Σ_(k=1) ^n k^2 =((n(n+1)(2n+1))/6) K_3 =Σ_(k=1) ^n k^3 =((n^2 (n+1)^2 )/4) K_4 =Σ_(k=1) ^n k^4 =((n(n+1)(2n+1)(3n^2 +3n−1))/(30))=((3n^2 +3n−1)/5)K_2 K_5 =Σ_(k=1) ^n k^5 =((n^2 (n+1)^2 (2n^2 +2n−1))/(12))=((2n^2 +2n−1)/3)K_3 K_6 =Σ_(k=1) ^n k^6 =((n(n+1)(2n+1)(3n^4 +6n^3 −3n+1))/(42))=((3n^4 +6n^3 −3n+1)/7)K_2 coef. of x^3 term: C_3 =C_(31) +C_(32) +C_(33) with C_(31) =Σ_(k≠j≠i) ^n a_(k,1) a_(j,1) a_(i,1) C_(32) =Σ_(k,j=1,j≠k) ^n a_(k,1) a_(j,2) C_(33) =Σ_(k=1) ^n a_(k,3) C_(31) =(1/6)[(Σ_(k=1) ^n a_(k,1) )^3 −Σ_(k=1) ^n a_(k,1) ^3 −3Σ_(i=1) ^n a_(i,1) ^2 (Σ_(k=1) ^n a_(k,1) −a_(i,1) )] =(1/6)[(Σ_(k=1) ^n a_(k,1) )^3 −Σ_(k=1) ^n a_(k,1) ^3 −3(Σ_(i=1) ^n a_(i,1) ^2 )(Σ_(k=1) ^n a_(k,1) )+3Σ_(i=1) ^n a_(i,1) ^3 ] =(1/6)(K_2 ^3 −3K_4 K_2 +2K_6 ) C_(32) =Σ_(k=1) ^n a_(k,1) Σ_(j=1,j≠k) ^n a_(j,2) =Σ_(k=1) ^n a_(k,1) (Σ_(j=1) ^n a_(j,2) −a_(k,2) ) =(Σ_(k=1) ^n a_(k,1) )(Σ_(j=1) ^n a_(j,2) )−Σ_(k=1) ^n a_(k,1) a_(k,2) =(Σ_(k=1) ^n k^2 )(Σ_(k=1) ^n ((k^3 (k−1))/2))−Σ_(k=1) ^n ((k^2 k^3 (k−1))/2) =(1/2)(K_2 K_4 −K_2 K_3 −K_6 +K_5 ) C_(33) =Σ_(k=1) ^n a_(k,3) =Σ_(k=1) ^n ((k^4 (k−1)(k−2))/6) =(1/6)(K_6 −3K_5 +2K_4 ) C_3 =(1/6)(K_2 ^3 −3K_2 K_4 +2K_6 )+(1/2)(K_2 K_4 −K_2 K_3 −K_6 +K_5 )+(1/6)(K_6 −3K_5 +2K_4 ) =(1/6)(K_2 ^3 −3K_2 K_3 +2K_4 ) =((n(n+1)(2n+1))/(36))[((n^2 (n+1)^2 (2n+1)^2 )/(36))−((3n^2 (n+1)^2 )/4)+((2(3n^2 +3n−1))/5)] =((n(n+1)(2n+1))/(36))[((n^2 (n+1)^2 (2n^2 +2n−13))/(18))+((2(3n^2 +3n−1))/5)] =(((n−1)n(n+1)(n+2)(2n+1)(10n^4 +20n^3 −35n^2 −45n+18))/(3240)) with n=100, C_3 =((99×100×101×102×201×(10×100^4 +20×10^3 −35×100^2 −45×100+18))/(3240)) =6 451 445 040 986 110](Q86068.png)
Commented by Prithwish Sen 1 last updated on 27/Mar/20
Commented by mr W last updated on 06/Apr/20
![coef. of x^4 term: C_4 =C_(41) +C_(42) +C_(43) +C_(44) +C_(45) with C_(41) =Σ_(k≠i≠j≠h) a_(k,1) a_(i,1) a_(j,1) a_(h,1) C_(42) =Σ_(k≠i≠j) a_(k,1) a_(i,1) a_(j,2) C_(43) =Σ_(k≠i) a_(k,1) a_(i,3) C_(44) =Σ_(k≠i) a_(k,2) a_(i,2) C_(45) =Σ_(k=1) ^n a_(k,4) ..... C_(42) =Σ_(k≠i≠j) a_(k,1) a_(i,1) a_(j,2) C_(43) =Σ_(k≠i) a_(k,1) a_(i,3) =(1/2)Σ_(k=1) ^n a_(k,1) (Σ_(i=1) ^n a_(i,3) −a_(k,3) ) =(1/2)[(Σ_(k=1) ^n a_(k,1) )(Σ_(i=1) ^n a_(i,3) )−Σ_(k=1) ^n a_(k,1) a_(k,3) ] =(1/2)[(Σ_(k=1) ^n k^2 )(Σ_(i=1) ^n ((k^4 (k−1)(k−2))/6))−Σ_(k=1) ^n ((k^6 (k−1))k−2))/6)] =(1/(12))[(Σ_(k=1) ^n k^2 )(Σ_(i=1) ^n k^4 (k−1)(k−2))−Σ_(k=1) ^n k^6 (k−1)(k−2)] =(1/(12))[(Σ_(k=1) ^n k^2 )(Σ_(i=1) ^n (k^6 −3k^5 +2k^4 ))−Σ_(k=1) ^n (k^8 −3k^7 +2k^6 )] =(1/(12))[K_2 (K_6 −3K_5 +2K_4 )−(K_8 −3K_7 +2K_6 )] =(1/(12))(K_2 K_6 −3K_2 K_5 +2K_2 K_4 −K_8 +3K_7 −2K_6 ) C_(44) =Σ_(k≠i) a_(k,2) a_(i,2) =(1/2)Σ_(k=1) ^n a_(k,2) (Σ_(i=1) ^n a_(i,2) −a_(k,2) ) =(1/2)[(Σ_(k=1) ^n a_(k,2) )^2 −Σ_(k=1) ^n a_(k,2) ^2 ] =(1/2)[(Σ_(k=1) ^n ((k^3 (k−1))/2))^2 −Σ_(k=1) ^n ((k^6 (k−1)^2 )/4)] =(1/8)[(K_4 −K_3 )^2 −(K_8 −2K_7 +K_6 )] =(1/8)(K_4 ^2 −2K_3 K_4 +K_3 ^2 −K_8 +2K_7 −K_6 ) C_(45) =Σ_(k=1) ^n a_(k,4) =Σ_(k=1) ^n ((k^5 (k−1)(k−2)(k−3))/(24)) =(1/(24))(K_8 −6K_7 +11K_6 −6K_5 ) ......](Q87871.png)
