Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 85909 by jagoll last updated on 26/Mar/20

$$\int {\sin }^{-1}\left(\sqrt{\frac{\mathrm{x}}{\mathrm{a}+\mathrm{x}}}\right)\mathrm{dx},\mathrm{a}>0$$

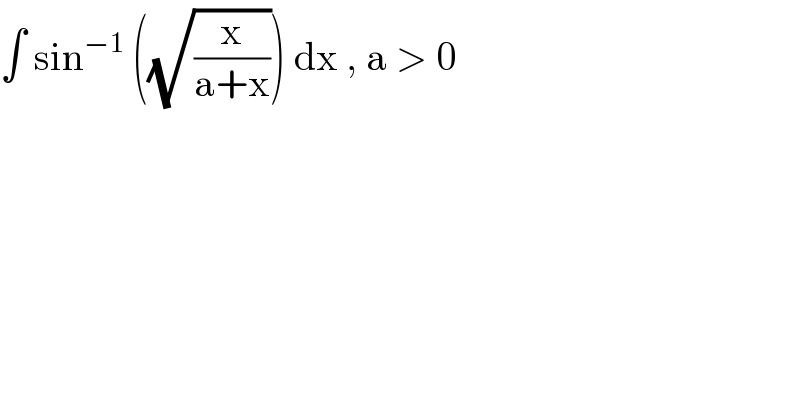
Commented byjohn santu last updated on 26/Mar/20

$$let\sqrt{\frac{x}{a+x}}=n\Rightarrow x=\frac{{an}^2}{1-n^2}$$ $$I=\int {\sin }^{-1}\left(n\right)\times \frac{2an}{{(1-n^2)}^2}dn$$ $$[h={\sin }^{-1}\left(n\right)\Rightarrow n=\sin h]$$ $$I=2a\int h\tan h\sec {}^{2}hdh$$ $$I=a(h\tan {}^{2}h-\int (\sec {}^{2}h-1)dh)$$ $$I=a(h\tan {}^{2}h-\tan h+h)+c$$ $$\therefore I=x{\sin }^{-1}\left(\sqrt{\frac{x}{a+x}}\right)-\sqrt{ax}+a{\sin }^{-1}\left(\sqrt{\frac{x}{a+x}}\right)+c$$

Commented byjagoll last updated on 26/Mar/20

$$\mathrm{thank}\mathrm{you}\mathrm{all}$$

Answered by TANMAY PANACEA. last updated on 26/Mar/20

$$x={atan}^2\alpha \to \frac{dx}{d\alpha }=a\times 2tan\alpha \times {sec}^2\alpha$$ $$\sqrt{\frac{{atan}^2\alpha }{a+{atan}^2\alpha }}=\sqrt{\frac{{sin}^2\alpha }{{cos}^2\alpha \times {sec}^2\alpha }}=sin\alpha$$ $$I=\int \alpha .2atan\alpha .{sec}^2\alpha d\alpha$$ $$\frac{I}{2a}=\alpha \int tan\alpha {sec}^2\alpha d\alpha -\int [\frac{d\alpha }{d\alpha }\int tan\alpha {sec}^2\alpha d\alpha ]d\alpha$$ $$=\alpha .\frac{{tan}^2\alpha }{2}-\frac{1}{2}\int ({sec}^2\alpha -1)d\alpha$$ $$=\frac{\alpha {tan}^2\alpha }{2}-\frac{tan\alpha }{2}+\frac{\alpha }{2}$$ $$now\alpha ={tan}^{-1}\sqrt{\frac{x}{a}}$$ $$I=(\frac{{tan}^{-1}\sqrt{\frac{x}{a}}\times \frac{x}{a}}{2}-\frac{\sqrt{\frac{x}{a}}}{2}+\frac{{tan}^{-1}\sqrt{\frac{x}{a}}}{2})\times 2a$$ $$I={xtan}^{-1}\sqrt{\frac{x}{a}}-a\sqrt{\frac{x}{a}}+{atan}^{-1}\sqrt{\frac{x}{a}}$$ $$=(x+a){tan}^{-1}\sqrt{\frac{x}{a}}-\sqrt{ax}$$ $$plscheck$$

Answered by Kunal12588 last updated on 26/Mar/20

$$I={xsin}^{-1}\sqrt{\frac{x}{a+x}}-\int x\times \frac{1}{\sqrt{1-\frac{x}{a+x}}}\times \frac{1}{2\sqrt{\frac{x}{a+x}}}\times \frac{a+x-x}{{(a+x)}^2}dx$$ $$={xsin}^{-1}\sqrt{\frac{x}{a+x}}-\int x\times \frac{\sqrt{a+x}}{\sqrt{a}}\times \frac{\sqrt{a+x}}{2\sqrt{x}}\times \frac{a}{{(a+x)}^2}dx$$ $$={xsin}^{-1}\sqrt{\frac{x}{a+x}}-\frac{1}{2}\sqrt{a}\int \sqrt{x}\times \frac{1}{a+x}dx$$ $$I_1=\int \frac{\sqrt{x}}{a+x}dx$$ $$\sqrt{x}=t$$ $$dx=2\sqrt{x}dt$$ $$I_1=2\int \frac{x}{a+x}dt=2\int \frac{t^2}{a+t^2}dt$$ $$=2\int \frac{a+t^2}{a+t^2}dt-2a\int \frac{dt}{a+t^2}$$ $$=2t-2a\times \frac{1}{\sqrt{a}}{tan}^{-1}\frac{t}{\sqrt{a}}+c$$ $$=2\sqrt{x}-2\sqrt{a}{tan}^{-1}\frac{\sqrt{x}}{\sqrt{a}}+c$$ $$I={xsin}^{-1}\sqrt{\frac{x}{a+x}}-\frac{1}{2}\sqrt{a}(2\sqrt{x}-2\sqrt{a}{tan}^{-1}\sqrt{\frac{x}{a}})+C$$ $$I={xsin}^{-1}\sqrt{\frac{x}{a+x}}-\sqrt{ax}+a{tan}^{-1}\sqrt{\frac{x}{a}}+C$$

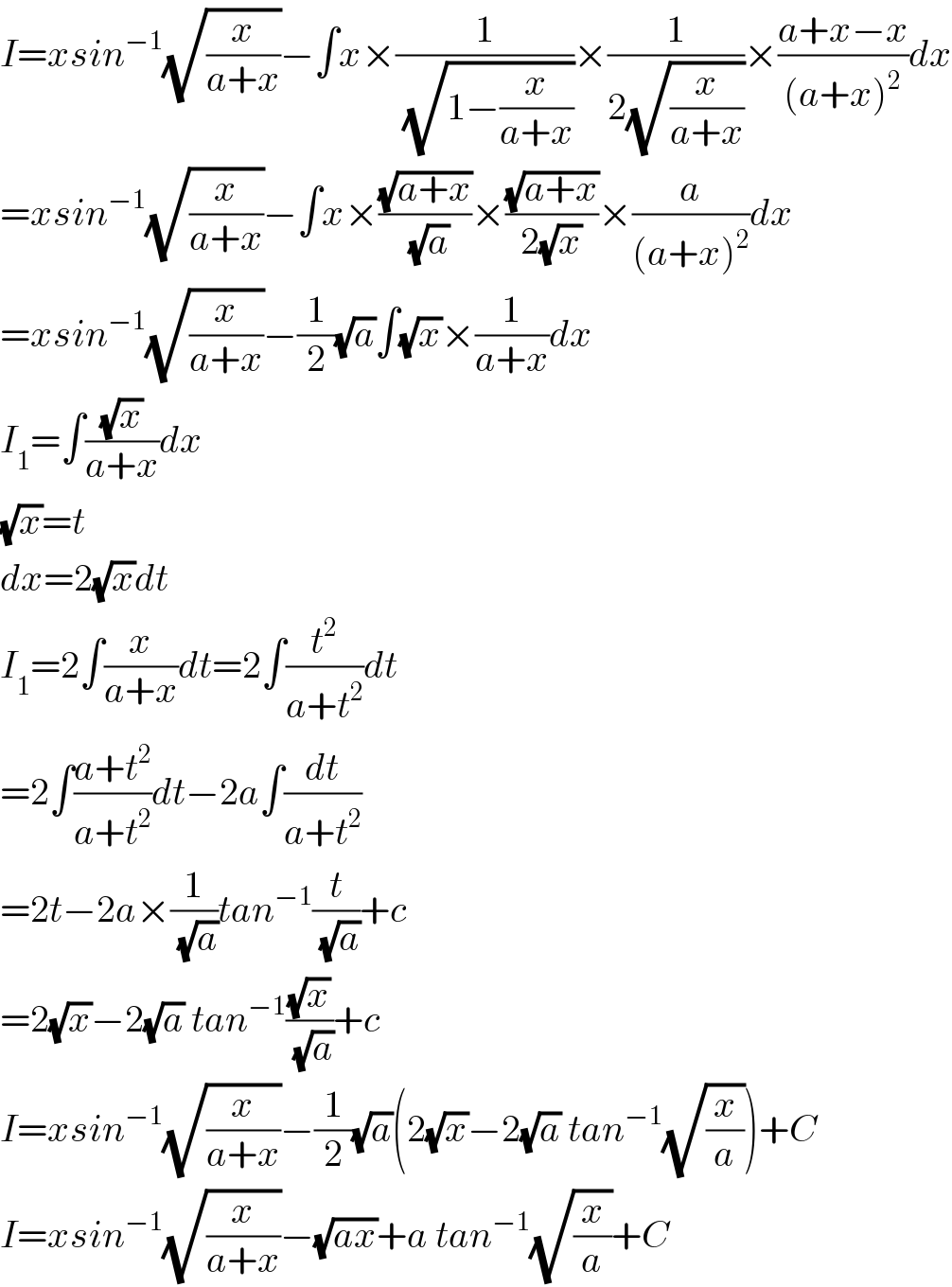
Commented byKunal12588 last updated on 26/Mar/20

$${sin}^{-1}\sqrt{\frac{x}{a+x}}={tan}^{-1}\sqrt{\frac{x}{a}}$$ $$soTanmaysiryouranswerisalsocorrect!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com