
Question and Answers Forum
Question Number 85914 by frc2crc last updated on 26/Mar/20
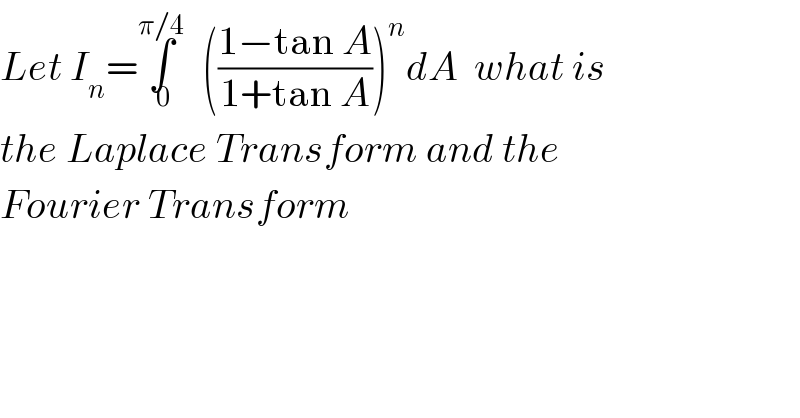
Answered by mind is power last updated on 26/Mar/20
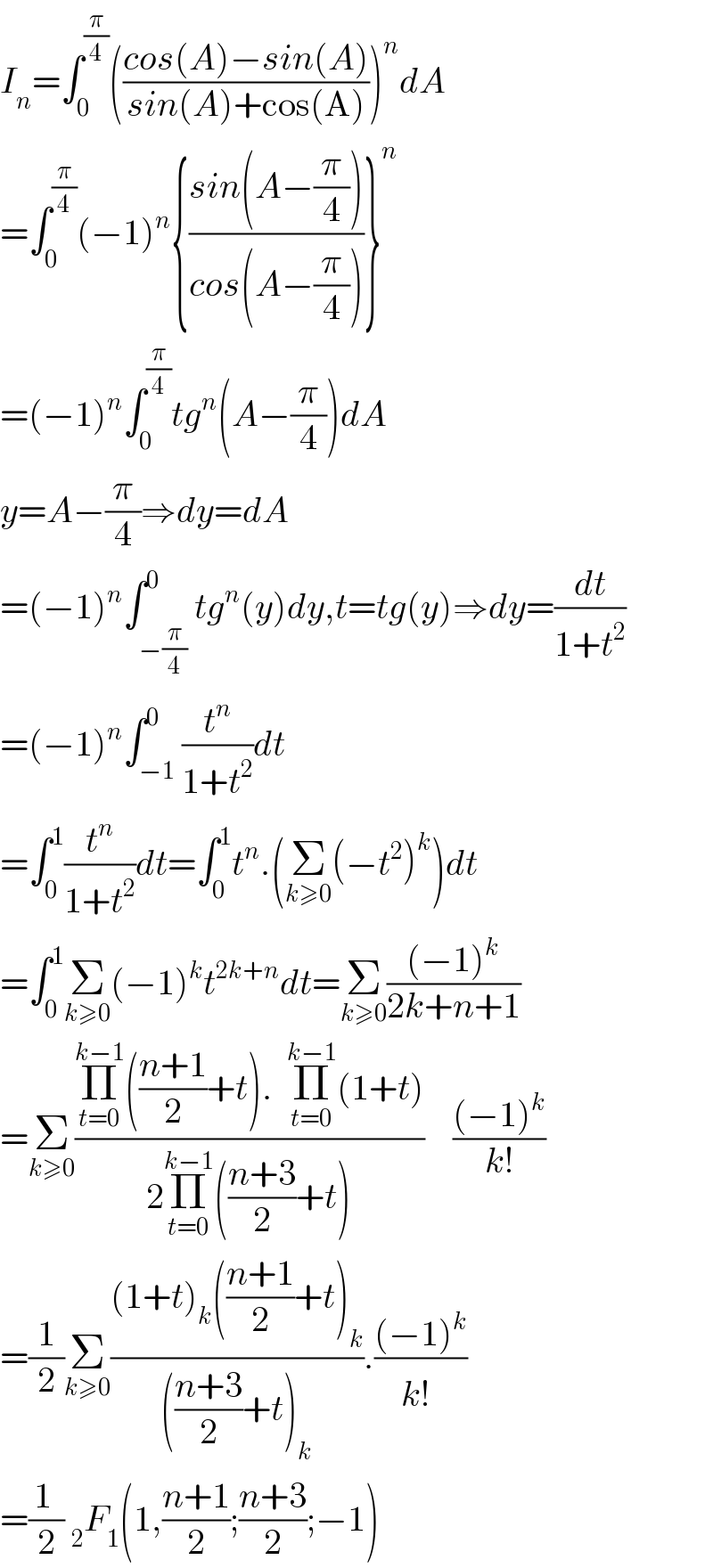
| ||
Question and Answers Forum | ||
Question Number 85914 by frc2crc last updated on 26/Mar/20 | ||
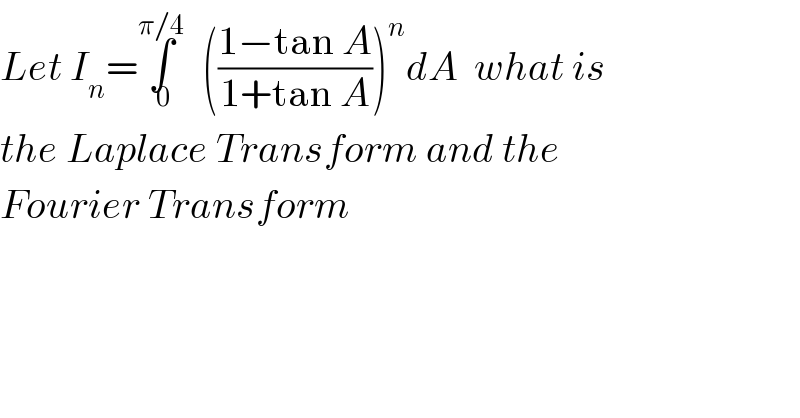 | ||
Answered by mind is power last updated on 26/Mar/20 | ||
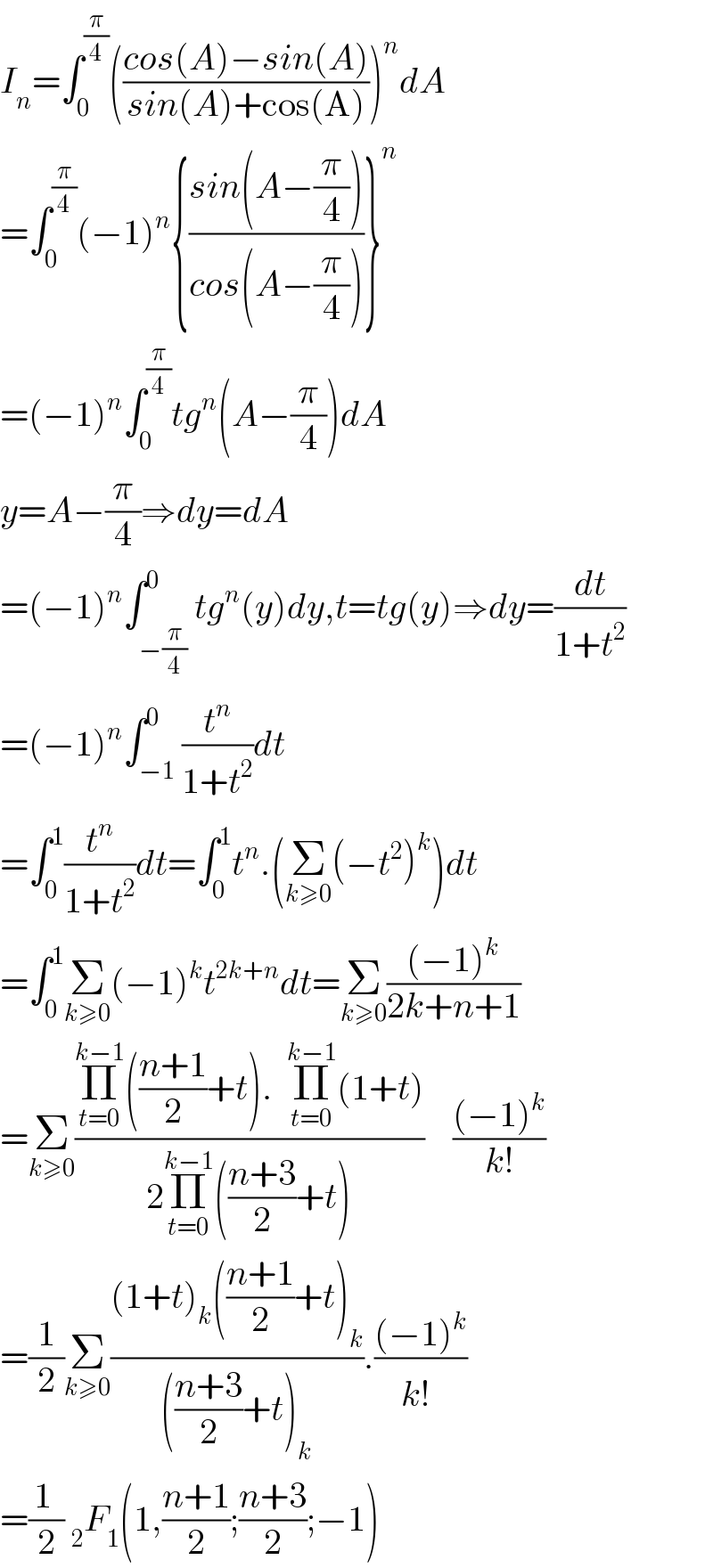 | ||
| ||