
Question and Answers Forum
Question Number 87046 by Tajaddin last updated on 02/Apr/20
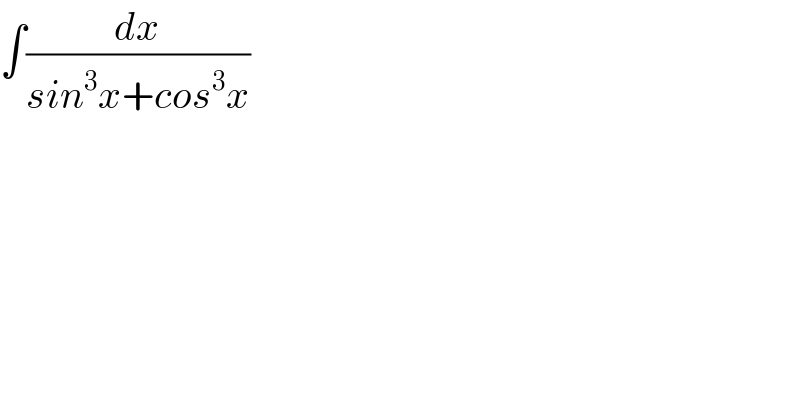
Answered by MJS last updated on 02/Apr/20
![∫(dx/(sin^3 x +cos^3 x))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−2∫((t^4 +2t^2 +1)/(t^6 −3t^4 −8t^3 +3t^2 −1))dt= =−2∫(((t^2 +1)^2 )/((t^2 −2t−1)(t^4 +2t^3 +2t^2 −2t+1)))dt= =−2∫(((t^2 +1)^2 )/((t^2 −1−(√2))(t−1+(√2))(t^2 +(1−(√3))t+2−(√3))(t^2 +(1+(√3))t+2+(√3))))dt= =−((√2)/3)∫(dt/(t−1−(√2)))+((√2)/3)∫(dt/(t−1+(√2)))− −((1−(√3))/3)∫(dt/(t^2 +(1−(√3))t+2−(√3)))− −((1+(√3))/3)∫(dt/(t^2 +(1+(√3))t+2+(√3)))= [now using formula] =((√2)/3)ln ((t−1+(√2))/(t−1−(√2))) +(2/3)(arctan ((1+(√3))t−1) +arctan ((1−(√3))t−1) now insert t=tan (x/2)](Q87053.png)
Commented by Ar Brandon last updated on 02/Apr/20
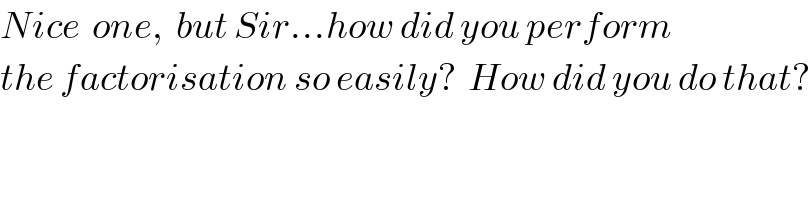
| ||
Question and Answers Forum | ||
Question Number 87046 by Tajaddin last updated on 02/Apr/20 | ||
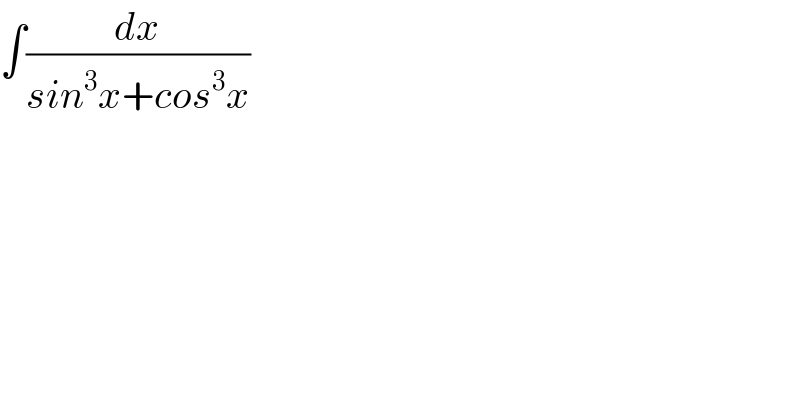 | ||
Answered by MJS last updated on 02/Apr/20 | ||
![∫(dx/(sin^3 x +cos^3 x))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−2∫((t^4 +2t^2 +1)/(t^6 −3t^4 −8t^3 +3t^2 −1))dt= =−2∫(((t^2 +1)^2 )/((t^2 −2t−1)(t^4 +2t^3 +2t^2 −2t+1)))dt= =−2∫(((t^2 +1)^2 )/((t^2 −1−(√2))(t−1+(√2))(t^2 +(1−(√3))t+2−(√3))(t^2 +(1+(√3))t+2+(√3))))dt= =−((√2)/3)∫(dt/(t−1−(√2)))+((√2)/3)∫(dt/(t−1+(√2)))− −((1−(√3))/3)∫(dt/(t^2 +(1−(√3))t+2−(√3)))− −((1+(√3))/3)∫(dt/(t^2 +(1+(√3))t+2+(√3)))= [now using formula] =((√2)/3)ln ((t−1+(√2))/(t−1−(√2))) +(2/3)(arctan ((1+(√3))t−1) +arctan ((1−(√3))t−1) now insert t=tan (x/2)](Q87053.png) | ||
| ||
Commented by Ar Brandon last updated on 02/Apr/20 | ||
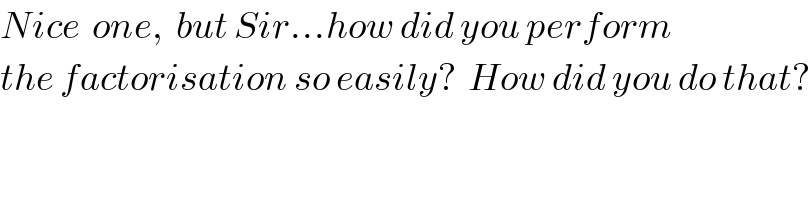 | ||