
Question and Answers Forum
Question Number 87168 by mathocean1 last updated on 03/Apr/20

Commented by john santu last updated on 03/Apr/20
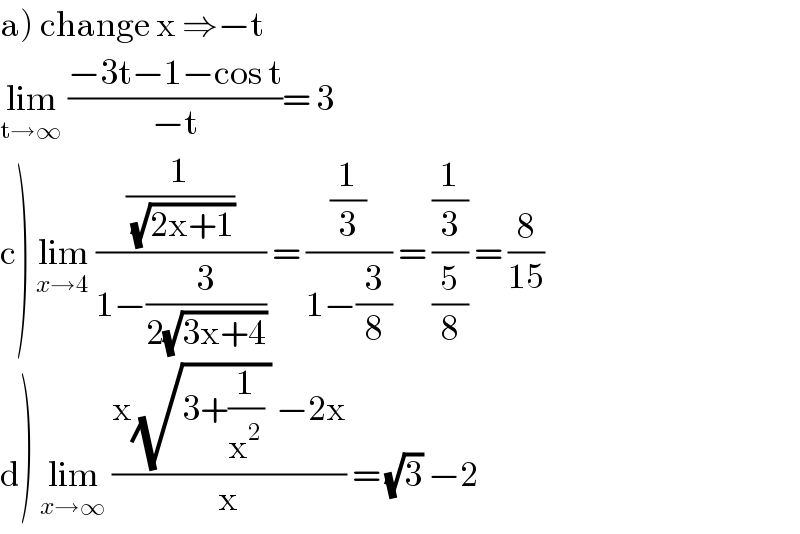
Commented by mathocean1 last updated on 03/Apr/20

Commented by john santu last updated on 03/Apr/20

Commented by mathocean1 last updated on 03/Apr/20

Commented by TANMAY PANACEA. last updated on 03/Apr/20

Commented by TANMAY PANACEA. last updated on 03/Apr/20

Commented by mathmax by abdo last updated on 03/Apr/20
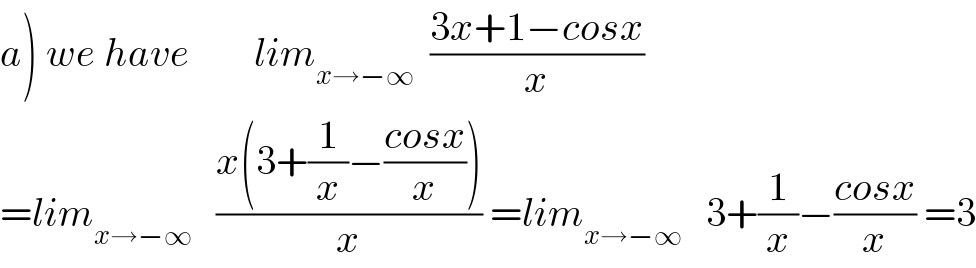
Commented by mathmax by abdo last updated on 03/Apr/20

Commented by mathmax by abdo last updated on 03/Apr/20
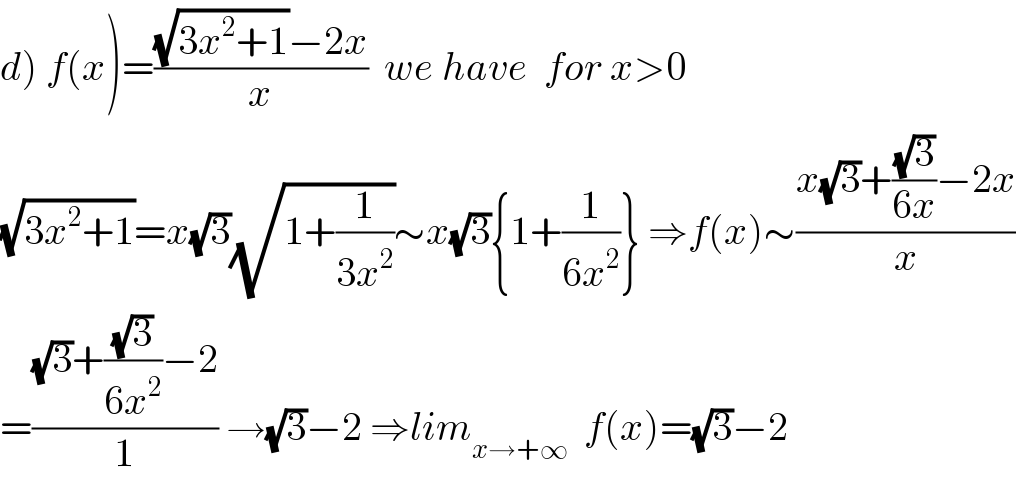
Commented by mathmax by abdo last updated on 03/Apr/20
![b) let f(x)=((x^2 +1)/(x[x])) changement x=−t give f(x)=((t^2 +1)/(−t[−t])) (x→−∞ ⇒t→ +∞) and we have [−t] =α−[t] with α =0 or −1 ⇒[−t]∼−[t]∼−t ⇒ lim_(x→−∞) f(x) =lim_(t→+∞) −((t^2 +1)/(t(−t))) =lim_(t→+∞) ((t^2 +1)/t^2 ) =1](Q87228.png)
Commented by john santu last updated on 03/Apr/20

Commented by john santu last updated on 03/Apr/20
![why E(x)= [ x ] ? E(x) = μ ?](Q87231.png)
Commented by mathmax by abdo last updated on 03/Apr/20

Commented by mathmax by abdo last updated on 03/Apr/20
![x =[x] +r with 0≤r<1 ⇒(x/([x])) =1+(r/([x])) ⇒(x/([x])) ∼ 1 (x→+∞)](Q87240.png)
Commented by mathocean1 last updated on 03/Apr/20

