Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 87194 by john santu last updated on 03/Apr/20

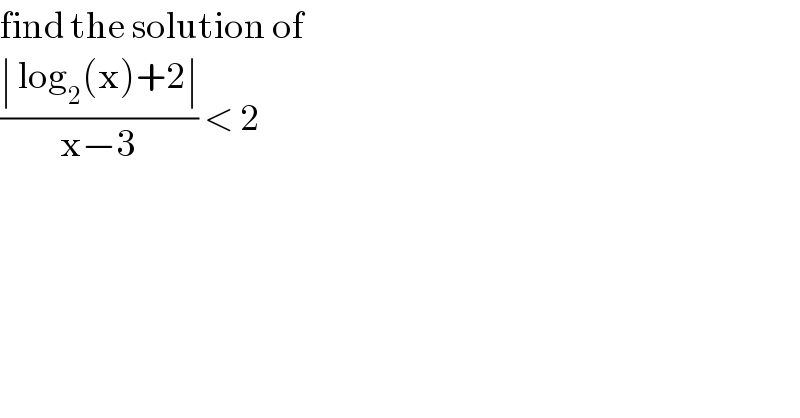
find the solution of ((∣ log_2 (x)+2∣)/(x−3)) < 2

$$\mathrm{find}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{of}\: \\ $$ $$\frac{\mid\:\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{2}\mid}{\mathrm{x}−\mathrm{3}}\:<\:\mathrm{2}\: \\ $$

Commented byTANMAY PANACEA. last updated on 03/Apr/20

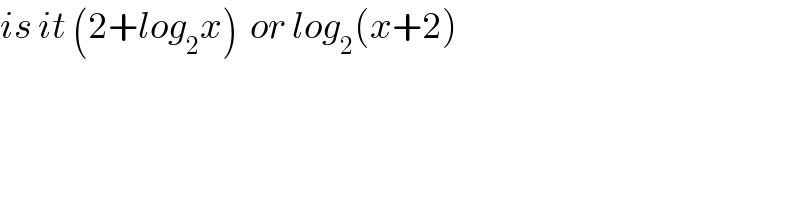
is it (2+log_2 x) or log_2 (x+2)

$${is}\:{it}\:\left(\mathrm{2}+{log}_{\mathrm{2}} {x}\right)\:\:{or}\:{log}_{\mathrm{2}} \left({x}+\mathrm{2}\right) \\ $$

Commented byjohn santu last updated on 03/Apr/20

2+ log_2 (x) sir

$$\mathrm{2}+\:\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}\right)\:\mathrm{sir} \\ $$

Commented byjohn santu last updated on 03/Apr/20

i can^′ t answer that

$$\mathrm{i}\:\mathrm{can}^{'} \mathrm{t}\:\mathrm{answer}\:\mathrm{that} \\ $$

Commented byjohn santu last updated on 03/Apr/20

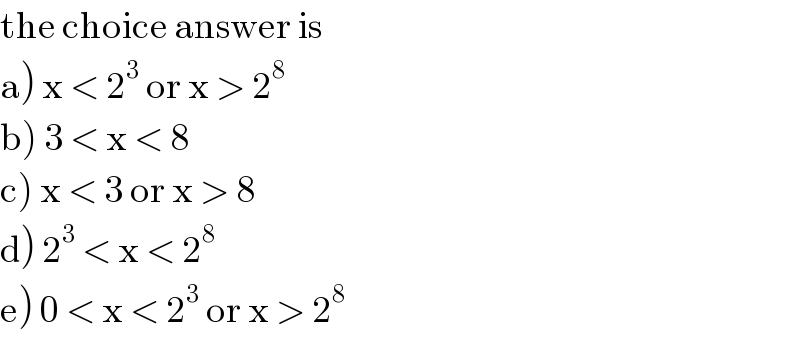
the choice answer is a) x < 2^3 or x > 2^8 b) 3 < x < 8 c) x < 3 or x > 8 d) 2^3 < x < 2^8 e) 0 < x < 2^3 or x > 2^8

$$\mathrm{the}\:\mathrm{choice}\:\mathrm{answer}\:\mathrm{is}\: \\ $$ $$\left.\mathrm{a}\right)\:\mathrm{x}\:<\:\mathrm{2}^{\mathrm{3}} \:\mathrm{or}\:\mathrm{x}\:>\:\mathrm{2}^{\mathrm{8}} \\ $$ $$\left.\mathrm{b}\right)\:\mathrm{3}\:<\:\mathrm{x}\:<\:\mathrm{8} \\ $$ $$\left.\mathrm{c}\right)\:\mathrm{x}\:<\:\mathrm{3}\:\mathrm{or}\:\mathrm{x}\:>\:\mathrm{8} \\ $$ $$\left.\mathrm{d}\right)\:\mathrm{2}^{\mathrm{3}} \:<\:\mathrm{x}\:<\:\mathrm{2}^{\mathrm{8}} \\ $$ $$\left.\mathrm{e}\right)\:\mathrm{0}\:<\:\mathrm{x}\:<\:\mathrm{2}^{\mathrm{3}} \:\mathrm{or}\:\mathrm{x}\:>\:\mathrm{2}^{\mathrm{8}} \\ $$

Commented byjagoll last updated on 03/Apr/20

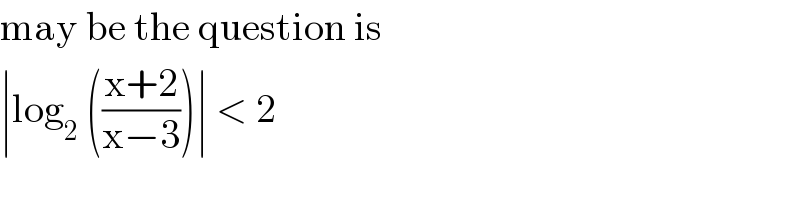
may be the question is ∣log_2 (((x+2)/(x−3)))∣ < 2

$$\mathrm{may}\:\mathrm{be}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\: \\ $$ $$\mid\mathrm{log}_{\mathrm{2}} \:\left(\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}−\mathrm{3}}\right)\mid\:<\:\mathrm{2} \\ $$

Commented byjagoll last updated on 03/Apr/20

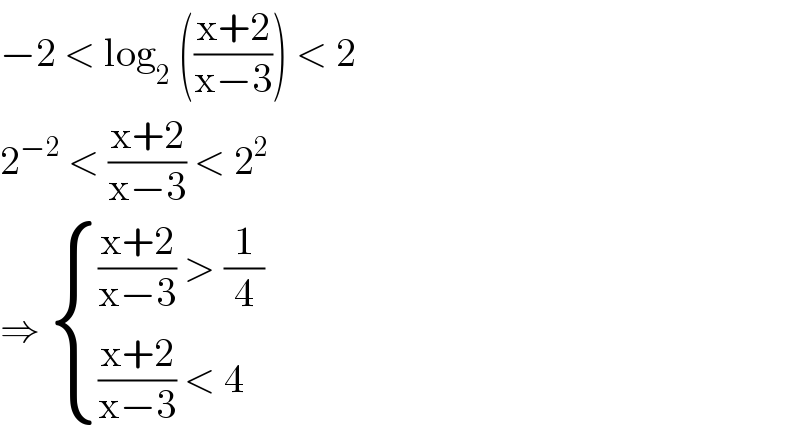
−2 < log_2 (((x+2)/(x−3))) < 2 2^(−2) < ((x+2)/(x−3)) < 2^2 ⇒ { ((((x+2)/(x−3)) > (1/4))),((((x+2)/(x−3)) < 4)) :}

$$−\mathrm{2}\:<\:\mathrm{log}_{\mathrm{2}} \:\left(\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}−\mathrm{3}}\right)\:<\:\mathrm{2} \\ $$ $$\mathrm{2}^{−\mathrm{2}} \:<\:\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}−\mathrm{3}}\:<\:\mathrm{2}^{\mathrm{2}} \\ $$ $$\Rightarrow\:\begin{cases}{\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}−\mathrm{3}}\:>\:\frac{\mathrm{1}}{\mathrm{4}}}\\{\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}−\mathrm{3}}\:<\:\mathrm{4}}\end{cases}\: \\ $$

Answered by TANMAY PANACEA. last updated on 03/Apr/20

((∣2+log_2 x∣)/(x−3))−2<0 1)x≠3 and x≠0 assume x=2^k k>0 ((∣2+k∣)/(2^k −3))−2 =((2+k)/(2^k −3))−2 when k=1 ((2+1)/(2−3))−2<0 when k=2 ((2+2)/(4−3))−2>0 (note here ) when k=3 ((2+3)/(8−3))−2<0 k=4 ((2+4)/(16−3))−2<0

$$\frac{\mid\mathrm{2}+{log}_{\mathrm{2}} {x}\mid}{{x}−\mathrm{3}}−\mathrm{2}<\mathrm{0} \\ $$ $$\left.\mathrm{1}\right){x}\neq\mathrm{3}\:\:\:{and}\:{x}\neq\mathrm{0} \\ $$ $${assume}\:{x}=\mathrm{2}^{{k}} \:\:\:{k}>\mathrm{0} \\ $$ $$\frac{\mid\mathrm{2}+{k}\mid}{\mathrm{2}^{{k}} −\mathrm{3}}−\mathrm{2} \\ $$ $$=\frac{\mathrm{2}+{k}}{\mathrm{2}^{{k}} −\mathrm{3}}−\mathrm{2} \\ $$ $${when}\:{k}=\mathrm{1} \\ $$ $$\frac{\mathrm{2}+\mathrm{1}}{\mathrm{2}−\mathrm{3}}−\mathrm{2}<\mathrm{0} \\ $$ $${when}\:{k}=\mathrm{2} \\ $$ $$\frac{\mathrm{2}+\mathrm{2}}{\mathrm{4}−\mathrm{3}}−\mathrm{2}>\mathrm{0}\:\:\left({note}\:{here}\:\right) \\ $$ $${when}\:{k}=\mathrm{3} \\ $$ $$\frac{\mathrm{2}+\mathrm{3}}{\mathrm{8}−\mathrm{3}}−\mathrm{2}<\mathrm{0} \\ $$ $${k}=\mathrm{4} \\ $$ $$\frac{\mathrm{2}+\mathrm{4}}{\mathrm{16}−\mathrm{3}}−\mathrm{2}<\mathrm{0} \\ $$ $$ \\ $$

Answered by MJS last updated on 03/Apr/20

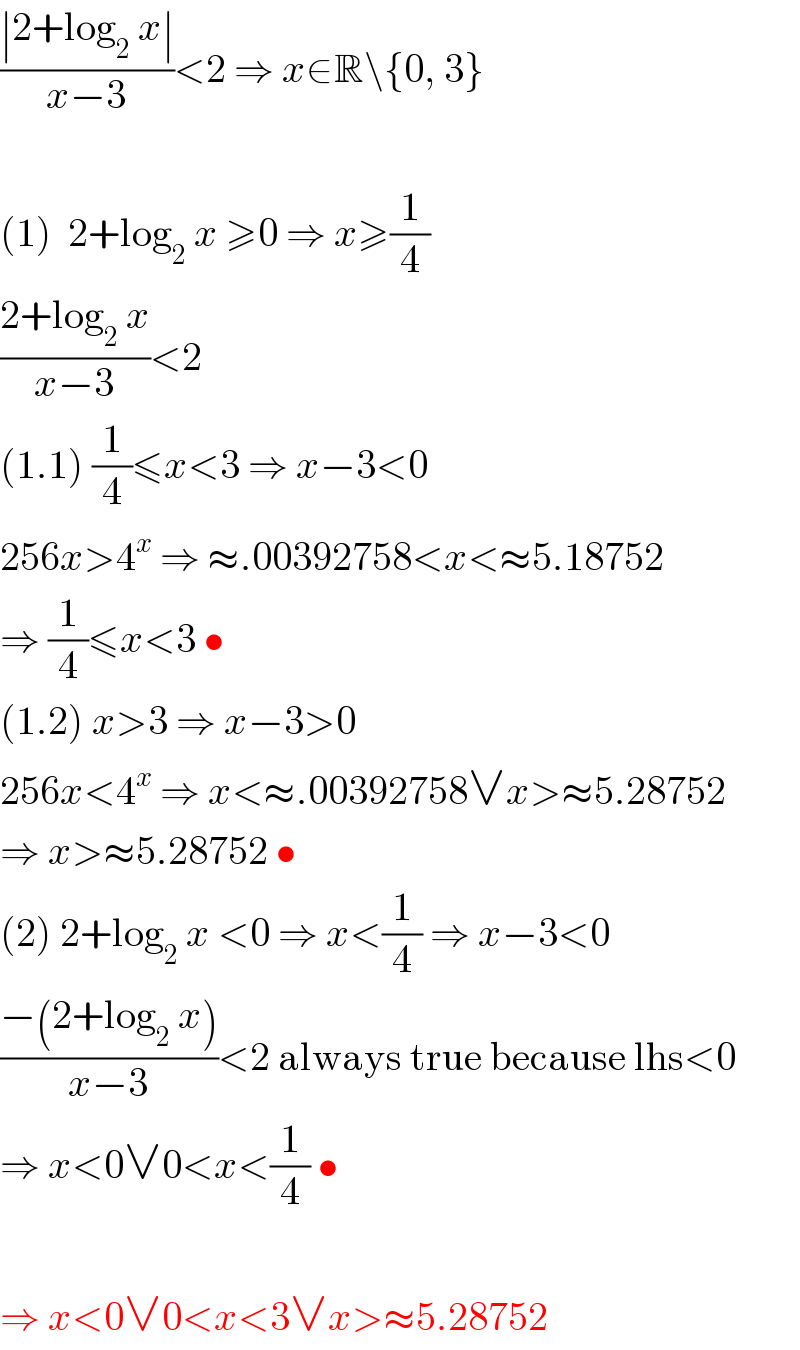
((∣2+log_2 x∣)/(x−3))<2 ⇒ x∈R\{0, 3} (1) 2+log_2 x ≥0 ⇒ x≥(1/4) ((2+log_2 x)/(x−3))<2 (1.1) (1/4)≤x<3 ⇒ x−3<0 256x>4^x ⇒ ≈.00392758<x<≈5.18752 ⇒ (1/4)≤x<3 • (1.2) x>3 ⇒ x−3>0 256x<4^x ⇒ x<≈.00392758∨x>≈5.28752 ⇒ x>≈5.28752 • (2) 2+log_2 x <0 ⇒ x<(1/4) ⇒ x−3<0 ((−(2+log_2 x))/(x−3))<2 always true because lhs<0 ⇒ x<0∨0<x<(1/4) • ⇒ x<0∨0<x<3∨x>≈5.28752

$$\frac{\mid\mathrm{2}+\mathrm{log}_{\mathrm{2}} \:{x}\mid}{{x}−\mathrm{3}}<\mathrm{2}\:\Rightarrow\:{x}\in\mathbb{R}\backslash\left\{\mathrm{0},\:\mathrm{3}\right\} \\ $$ $$ \\ $$ $$\left(\mathrm{1}\right)\:\:\mathrm{2}+\mathrm{log}_{\mathrm{2}} \:{x}\:\geqslant\mathrm{0}\:\Rightarrow\:{x}\geqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$ $$\frac{\mathrm{2}+\mathrm{log}_{\mathrm{2}} \:{x}}{{x}−\mathrm{3}}<\mathrm{2} \\ $$ $$\left(\mathrm{1}.\mathrm{1}\right)\:\frac{\mathrm{1}}{\mathrm{4}}\leqslant{x}<\mathrm{3}\:\Rightarrow\:{x}−\mathrm{3}<\mathrm{0} \\ $$ $$\mathrm{256}{x}>\mathrm{4}^{{x}} \:\Rightarrow\:\approx.\mathrm{00392758}<{x}<\approx\mathrm{5}.\mathrm{18752} \\ $$ $$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{4}}\leqslant{x}<\mathrm{3}\:\bullet \\ $$ $$\left(\mathrm{1}.\mathrm{2}\right)\:{x}>\mathrm{3}\:\Rightarrow\:{x}−\mathrm{3}>\mathrm{0} \\ $$ $$\mathrm{256}{x}<\mathrm{4}^{{x}} \:\Rightarrow\:{x}<\approx.\mathrm{00392758}\vee{x}>\approx\mathrm{5}.\mathrm{28752} \\ $$ $$\Rightarrow\:{x}>\approx\mathrm{5}.\mathrm{28752}\:\bullet \\ $$ $$\left(\mathrm{2}\right)\:\mathrm{2}+\mathrm{log}_{\mathrm{2}} \:{x}\:<\mathrm{0}\:\Rightarrow\:{x}<\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:{x}−\mathrm{3}<\mathrm{0} \\ $$ $$\frac{−\left(\mathrm{2}+\mathrm{log}_{\mathrm{2}} \:{x}\right)}{{x}−\mathrm{3}}<\mathrm{2}\:\mathrm{always}\:\mathrm{true}\:\mathrm{because}\:\mathrm{lhs}<\mathrm{0} \\ $$ $$\Rightarrow\:{x}<\mathrm{0}\vee\mathrm{0}<{x}<\frac{\mathrm{1}}{\mathrm{4}}\:\bullet \\ $$ $$ \\ $$ $$\Rightarrow\:{x}<\mathrm{0}\vee\mathrm{0}<{x}<\mathrm{3}\vee{x}>\approx\mathrm{5}.\mathrm{28752} \\ $$

Commented byMJS last updated on 03/Apr/20

even if the question is wrong, we can solve it

$$\mathrm{even}\:\mathrm{if}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{wrong},\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it} \\ $$

Commented byjagoll last updated on 03/Apr/20

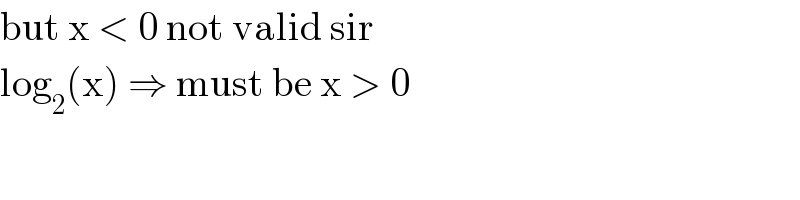
but x < 0 not valid sir log_2 (x) ⇒ must be x > 0

$$\mathrm{but}\:\mathrm{x}\:<\:\mathrm{0}\:\mathrm{not}\:\mathrm{valid}\:\mathrm{sir} \\ $$ $$\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}\right)\:\Rightarrow\:\mathrm{must}\:\mathrm{be}\:\mathrm{x}\:>\:\mathrm{0} \\ $$

Commented byMJS last updated on 03/Apr/20

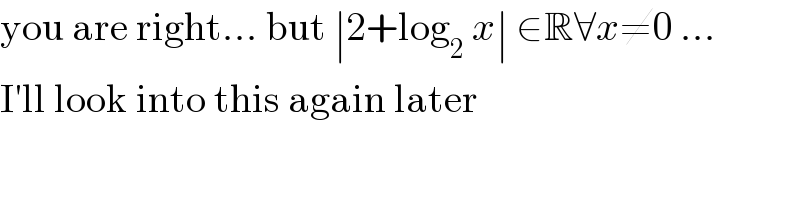
you are right... but ∣2+log_2 x∣ ∈R∀x≠0 ... I′ll look into this again later

$$\mathrm{you}\:\mathrm{are}\:\mathrm{right}...\:\mathrm{but}\:\mid\mathrm{2}+\mathrm{log}_{\mathrm{2}} \:{x}\mid\:\in\mathbb{R}\forall{x}\neq\mathrm{0}\:... \\ $$ $$\mathrm{I}'\mathrm{ll}\:\mathrm{look}\:\mathrm{into}\:\mathrm{this}\:\mathrm{again}\:\mathrm{later} \\ $$

Commented byMJS last updated on 03/Apr/20

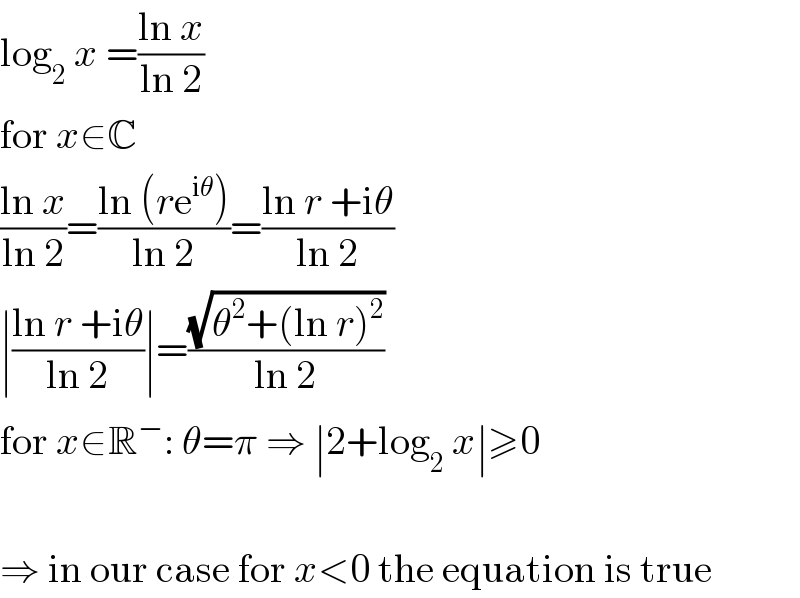
log_2 x =((ln x)/(ln 2)) for x∈C ((ln x)/(ln 2))=((ln (re^(iθ) ))/(ln 2))=((ln r +iθ)/(ln 2)) ∣((ln r +iθ)/(ln 2))∣=((√(θ^2 +(ln r)^2 ))/(ln 2)) for x∈R^− : θ=π ⇒ ∣2+log_2 x∣≥0 ⇒ in our case for x<0 the equation is true

$$\mathrm{log}_{\mathrm{2}} \:{x}\:=\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{2}} \\ $$ $$\mathrm{for}\:{x}\in\mathbb{C} \\ $$ $$\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{2}}=\frac{\mathrm{ln}\:\left({r}\mathrm{e}^{\mathrm{i}\theta} \right)}{\mathrm{ln}\:\mathrm{2}}=\frac{\mathrm{ln}\:{r}\:+\mathrm{i}\theta}{\mathrm{ln}\:\mathrm{2}} \\ $$ $$\mid\frac{\mathrm{ln}\:{r}\:+\mathrm{i}\theta}{\mathrm{ln}\:\mathrm{2}}\mid=\frac{\sqrt{\theta^{\mathrm{2}} +\left(\mathrm{ln}\:{r}\right)^{\mathrm{2}} }}{\mathrm{ln}\:\mathrm{2}} \\ $$ $$\mathrm{for}\:{x}\in\mathbb{R}^{−} :\:\theta=\pi\:\Rightarrow\:\mid\mathrm{2}+\mathrm{log}_{\mathrm{2}} \:{x}\mid\geqslant\mathrm{0} \\ $$ $$ \\ $$ $$\Rightarrow\:\mathrm{in}\:\mathrm{our}\:\mathrm{case}\:\mathrm{for}\:{x}<\mathrm{0}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{true} \\ $$

Commented byjohn santu last updated on 03/Apr/20

ooo if x ∈C sir. so the choice answer nothing correct sir

$$\mathrm{ooo}\:\mathrm{if}\:\mathrm{x}\:\in\mathbb{C}\:\mathrm{sir}.\: \\ $$ $$\mathrm{so}\:\mathrm{the}\:\mathrm{choice}\:\mathrm{answer}\:\mathrm{nothing}\:\mathrm{correct} \\ $$ $$\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com