Question and Answers Forum
Question Number 87243 by john santu last updated on 03/Apr/20
Commented by jagoll last updated on 04/Apr/20
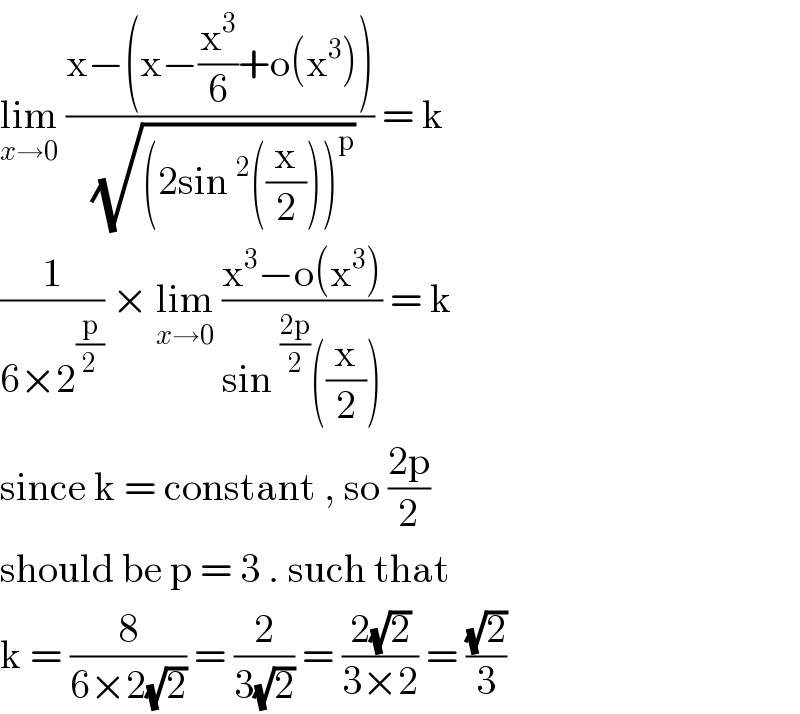
Answered by mr W last updated on 04/Apr/20
Commented by jagoll last updated on 04/Apr/20
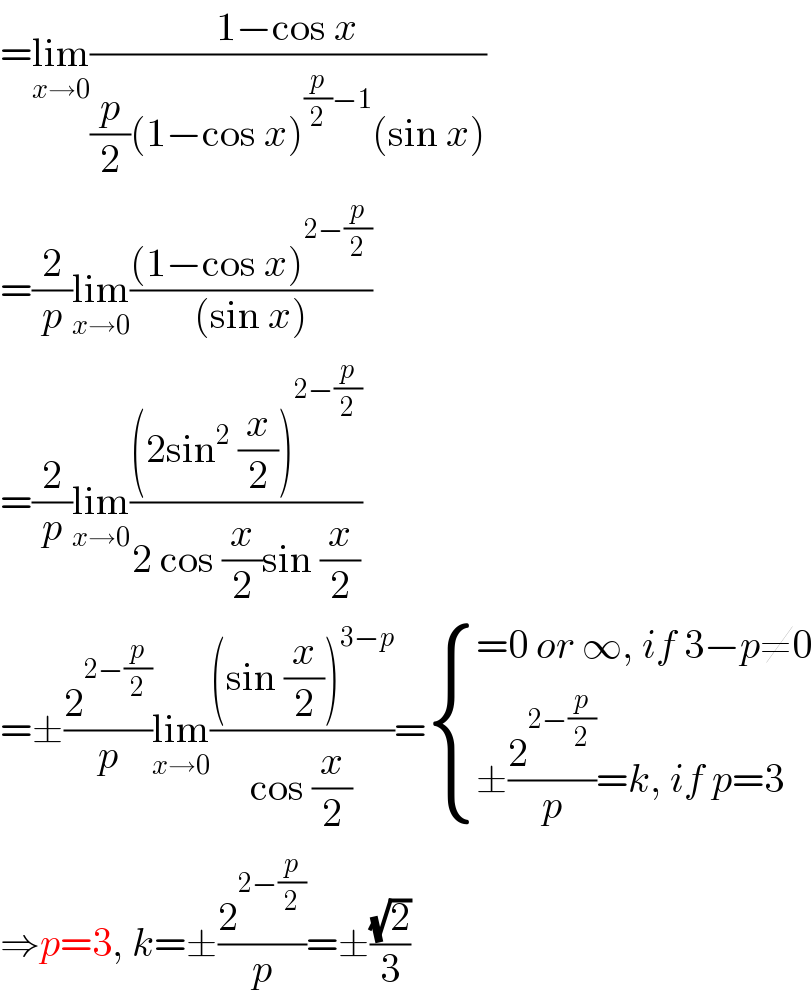
![why (d/dx) [(√((1−cos x)^p )) ] = (p/2)(1−cos x)^((p/2)−1) (−sin x) ? not (p/2) (1−cos x)^((p/2)−1) (+ sin x) ? mr w?](Q87334.png)
Commented by mr W last updated on 04/Apr/20
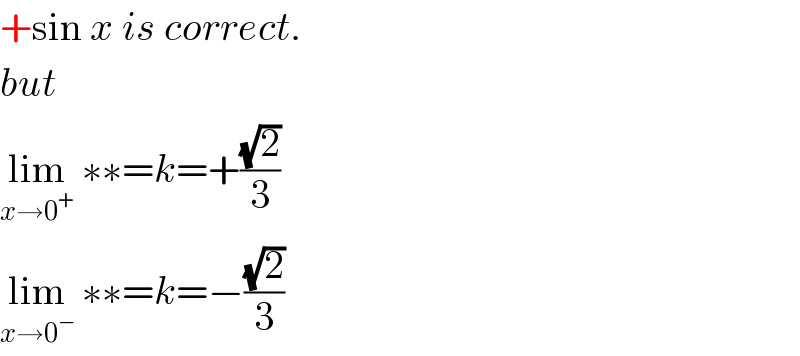
Commented by john santu last updated on 04/Apr/20

Commented by mr W last updated on 04/Apr/20