
Question and Answers Forum
Question Number 87296 by ajfour last updated on 03/Apr/20
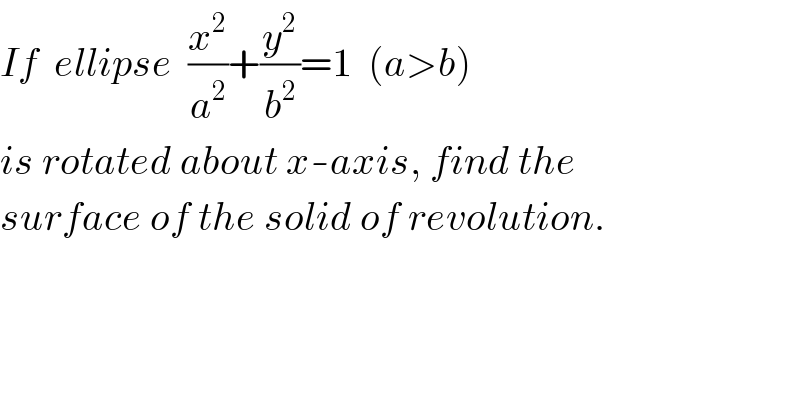
Answered by mr W last updated on 04/Apr/20
![let μ=(b/a) x=a cos θ y=b sin θ dx=−a sin θ dθ dy=b cos θ dθ ds=(√((dx)^2 +(dy)^2 ))=(√(a^2 sin^2 θ+b^2 cos^2 θ))dθ S=2×2π∫_0 ^(π/2) b sin θ (√(a^2 sin^2 θ+b^2 cos^2 θ))dθ =4πab∫_0 ^(π/2) sin θ (√(sin^2 θ+μ^2 cos^2 θ))dθ =4πab∫_(π/2) ^0 (√(1−(1−μ^2 )cos^2 θ))d(cos θ) =4πab∫_0 ^1 (√(1−kt^2 ))dt with k=1−μ^2 , t=cos θ =... =4πab[((sin^(−1) (√k)t)/(2(√k)))+((t(√(1−kt^2 )))/2)]_0 ^1 =4πab[((sin^(−1) (√k))/(2(√k)))+((√(1−k))/2)] =2πab[((sin^(−1) (√(1−μ^2 )))/(√(1−μ^2 )))+μ] with μ=(b/a) with a=b ⇒sphere a=b=R,μ=1 S=2πR^2 (1+1)=4πR^2](Q87355.png)
Commented byajfour last updated on 04/Apr/20

| ||
Question and Answers Forum | ||
Question Number 87296 by ajfour last updated on 03/Apr/20 | ||
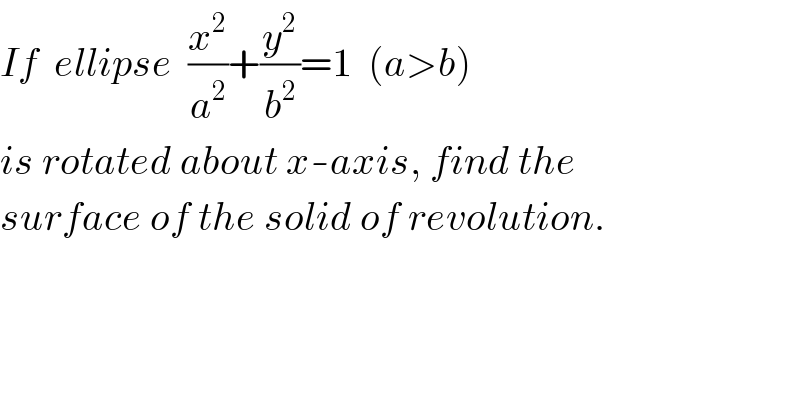 | ||
Answered by mr W last updated on 04/Apr/20 | ||
![let μ=(b/a) x=a cos θ y=b sin θ dx=−a sin θ dθ dy=b cos θ dθ ds=(√((dx)^2 +(dy)^2 ))=(√(a^2 sin^2 θ+b^2 cos^2 θ))dθ S=2×2π∫_0 ^(π/2) b sin θ (√(a^2 sin^2 θ+b^2 cos^2 θ))dθ =4πab∫_0 ^(π/2) sin θ (√(sin^2 θ+μ^2 cos^2 θ))dθ =4πab∫_(π/2) ^0 (√(1−(1−μ^2 )cos^2 θ))d(cos θ) =4πab∫_0 ^1 (√(1−kt^2 ))dt with k=1−μ^2 , t=cos θ =... =4πab[((sin^(−1) (√k)t)/(2(√k)))+((t(√(1−kt^2 )))/2)]_0 ^1 =4πab[((sin^(−1) (√k))/(2(√k)))+((√(1−k))/2)] =2πab[((sin^(−1) (√(1−μ^2 )))/(√(1−μ^2 )))+μ] with μ=(b/a) with a=b ⇒sphere a=b=R,μ=1 S=2πR^2 (1+1)=4πR^2](Q87355.png) | ||
| ||
Commented byajfour last updated on 04/Apr/20 | ||
 | ||