Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 87325 by M±th+et£s last updated on 04/Apr/20

$$1)\int e^{\sqrt{x}}dx$$$$2)\int \frac{\sqrt{sin\left(x\right)}}{\sqrt{sin\left(x\right)}+\sqrt{cos\left(x\right)}}dx$$

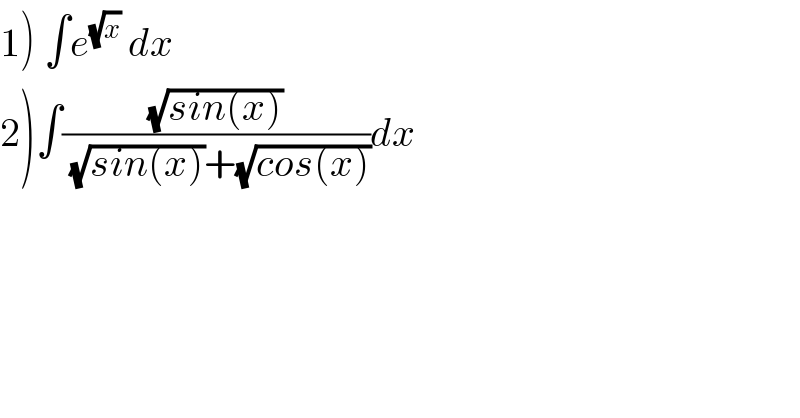
Commented by Serlea last updated on 04/Apr/20

$$1)\int {\mathrm{e}}^{\sqrt{\mathrm{x}}}\mathrm{dx}$$$$\mathrm{let}\sqrt{\mathrm{x}}=\mathrm{Y}$$$$\mathrm{x}={\mathrm{y}}^2$$$$\mathrm{dx}={\mathrm{y}}^2\mathrm{dy}$$$$\int {\mathrm{e}}^{\sqrt{\mathrm{x}}}\mathrm{dx}=\int {\mathrm{e}}^{\mathrm{y}}\left(2\mathrm{ydy}\right)$$$$=\int {2\mathrm{ye}}^{\mathrm{y}}\mathrm{dy}$$$$\mathrm{U}=2\mathrm{y}{\mathrm{U}}^{\prime }=2$$$${\mathrm{V}}^{\prime }={\mathrm{e}}^{\mathrm{y}}\mathrm{V}={\mathrm{e}}^{\mathrm{y}}$$$$$$$$\int {2\mathrm{ye}}^{\mathrm{y}}\mathrm{dy}={2\mathrm{Ye}}^{\mathrm{y}}-\int {2\mathrm{e}}^{\mathrm{y}}$$$$={2\mathrm{Ye}}^{\mathrm{y}}-{2\mathrm{e}}^{\mathrm{y}}$$$$={2\mathrm{e}}^{\mathrm{y}}(\mathrm{y}-1)$$$$={2\mathrm{e}}^{\sqrt{\mathrm{x}}}(\sqrt{\mathrm{x}}-1)$$$$$$

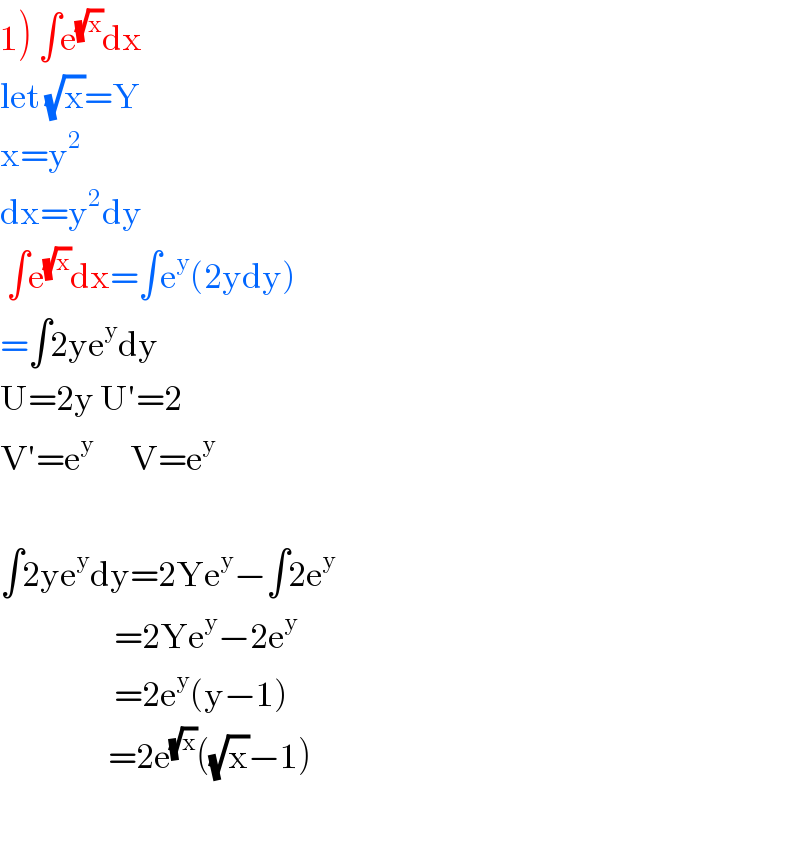
Commented by peter frank last updated on 04/Apr/20

$$qn2limit?$$$$$$

Commented by M±th+et£s last updated on 04/Apr/20

$$nosir$$

Answered by MJS last updated on 04/Apr/20

$$2)$$$$\int \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}dx=$$$$[t=\sqrt{\tan x}\to dx={2\cos }^{2}x\sqrt{\tan x}dt]$$$$=2\int \frac{t^2}{(t^4+1)(t+1)}dt=$$$$=-\frac{1-\sqrt{2}}{2}\int \frac{t+1}{t^2-\sqrt{2}t+1}dt-\frac{1+\sqrt{2}}{2}\int \frac{t+1}{t^2+\sqrt{2}t+1}dt+\int \frac{dt}{t+1}$$$$\mathrm{now}\mathrm{it}\mathrm{should}\mathrm{be}\mathrm{easy}$$

Commented by peter frank last updated on 04/Apr/20

$$thankyou$$

Commented by M±th+et£s last updated on 04/Apr/20

$$thankyou$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com