Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 87340 by john santu last updated on 04/Apr/20

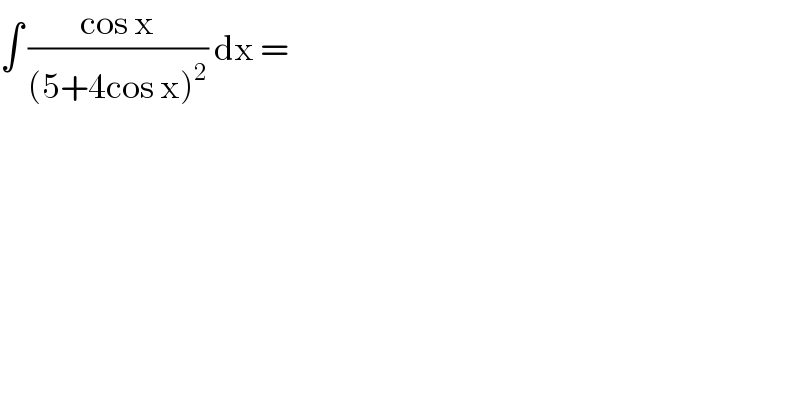
∫ ((cos x)/((5+4cos x)^2 )) dx =

$$\int\:\frac{\mathrm{cos}\:\mathrm{x}}{\left(\mathrm{5}+\mathrm{4cos}\:\mathrm{x}\right)^{\mathrm{2}} }\:\mathrm{dx}\:= \\ $$

Commented by john santu last updated on 04/Apr/20

dear mr Mjs. whether methods besides weierstrass substitution?

$$\mathrm{dear}\:\mathrm{mr}\:\mathrm{Mjs}.\:\mathrm{whether}\:\mathrm{methods}\: \\ $$$$\mathrm{besides}\:\mathrm{weierstrass}\:\mathrm{substitution}? \\ $$

Commented by MJS last updated on 04/Apr/20

all other methods are super complicated

$$\mathrm{all}\:\mathrm{other}\:\mathrm{methods}\:\mathrm{are}\:\mathrm{super}\:\mathrm{complicated} \\ $$

Commented by mathmax by abdo last updated on 04/Apr/20

I =∫ ((cosx)/((5+4cosx)^2 ))dx ⇒I =(1/(25))∫ ((cosx)/((1+(4/5)cosx)^2 ))dx let f(a) =∫ (dx/(1+acosx)) with 0<a<1 ⇒f^′ (a) =−∫ ((cosx)/((1+acosx)^2 ))dx ⇒ ∫ ((cosx)/((1+acosx)^2 ))dx =−f^′ (a) and I =−(1/(25))f^′ ((4/5)) let explicit f(a) f(a) =_(tan((x/2))=t) ∫ ((2dt)/((1+t^2 )(1+a((1−t^2 )/(1+t^2 ))))) =∫ ((2dt)/(1+t^2 +a−at^2 )) =∫ ((2dt)/((1−a)t^2 +1+a)) =(2/(1−a))∫ (dt/(t^2 +((1+a)/(1−a)))) =_(t=(√((1+a)/(1−a)))u) (2/(1−a))×((1−a)/(1+a)) ∫ (1/(1+u^2 ))×(√((1+a)/(1−a)))du =(2/(√(1−a^2 ))) arctan((√((1−a)/(1+a)))t) +C =(2/(√(1−a^2 ))) arctan((√((1−a)/(1+a)))tan((x/2))) +C ⇒ f^′ (a) =(2(1−a^2 )^(−(1/2)) )^′ arctan((√((1−a)/(1+a)))tan((x/2))) +(2/(√(1−a^2 ))) { ((((√((1−a)/(1+a)))tan((x/2))^′ )/(1+((1−a)/(1+a))tan^2 ((x/2))))} =−(−2a)(1−a^2 )^(−(3/2)) arctan((√((1−a)/(1+a)))tan((x/2))) +(2/(√(1−a^2 )))tan((x/2))×(1/(1+((1−a)/(1+a))tan^2 ((x/2))))×(((((1−a)/(1+a)))^′ )/(2(√((1−a)/(1+a))))) =2a(1−a^2 )^(−(3/2)) arctan((√((1−a)/(1+a)))tan((x/2))) +(2/(√(1−a^2 )))tan((x/2))×(1/(1+((1−a)/(1+a))tan^2 ((x/2))))×((−2)/((1+a)^2 ×2(√((1−a)/(1+a))))) I =−(1/(25))f^′ ((4/5))

$${I}\:=\int\:\:\frac{{cosx}}{\left(\mathrm{5}+\mathrm{4}{cosx}\right)^{\mathrm{2}} }{dx}\:\Rightarrow{I}\:=\frac{\mathrm{1}}{\mathrm{25}}\int\:\:\frac{{cosx}}{\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{5}}{cosx}\right)^{\mathrm{2}} }{dx} \\ $$$${let}\:{f}\left({a}\right)\:=\int\:\:\:\:\frac{{dx}}{\mathrm{1}+{acosx}}\:\:{with}\:\mathrm{0}<{a}<\mathrm{1}\:\Rightarrow{f}^{'} \left({a}\right)\:=−\int\:\:\frac{{cosx}}{\left(\mathrm{1}+{acosx}\right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\int\:\:\frac{{cosx}}{\left(\mathrm{1}+{acosx}\right)^{\mathrm{2}} }{dx}\:=−{f}^{'} \left({a}\right)\:{and}\:{I}\:=−\frac{\mathrm{1}}{\mathrm{25}}{f}^{'} \left(\frac{\mathrm{4}}{\mathrm{5}}\right)\:{let}\:{explicit}\:{f}\left({a}\right) \\ $$$${f}\left({a}\right)\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\int\:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$=\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} +{a}−{at}^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}−{a}\right){t}^{\mathrm{2}} \:+\mathrm{1}+{a}}\:=\frac{\mathrm{2}}{\mathrm{1}−{a}}\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}} \\ $$$$=_{{t}=\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}{u}} \:\:\:\:\frac{\mathrm{2}}{\mathrm{1}−{a}}×\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}\:\int\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }×\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}{du} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:{arctan}\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}{t}\right)\:+{C} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:{arctan}\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)\:+{C}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)\:=\left(\mathrm{2}\left(\mathrm{1}−{a}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)^{'} \:{arctan}\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right) \\ $$$$+\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:\left\{\:\:\frac{\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}{tan}\left(\frac{{x}}{\mathrm{2}}\right)^{'} \right.}{\mathrm{1}+\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\right\} \\ $$$$=−\left(−\mathrm{2}{a}\right)\left(\mathrm{1}−{a}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{arctan}\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right) \\ $$$$+\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{tan}\left(\frac{{x}}{\mathrm{2}}\right)×\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}×\frac{\left(\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}\right)^{'} }{\mathrm{2}\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}} \\ $$$$=\mathrm{2}{a}\left(\mathrm{1}−{a}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{arctan}\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right) \\ $$$$+\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{tan}\left(\frac{{x}}{\mathrm{2}}\right)×\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}×\frac{−\mathrm{2}}{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} ×\mathrm{2}\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}} \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{25}}{f}^{'} \left(\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$

Answered by ajfour last updated on 04/Apr/20

let tan (x/2)=t ⇒ (1/2)(sec^2 (x/2))dx=dt ⇒ dx=((2dt)/(1+t^2 )) , cos x=((1−t^2 )/(1+t^2 )) I=∫(((((1−t^2 )/(1+t^2 )))(((2dt)/(1+t^2 ))))/((5+((4−4t^2 )/(1+t^2 )))^2 )) I= 2∫((1−t^2 )/((9+t^2 )^2 ))dt now let t=3tan θ dt=3sec^2 θdθ I=2∫((1−9tan^2 θ)/(81sec^4 θ))(3sec^2 θdθ) say tan θ=z I=(2/(27))∫cos^2 θdθ−(1/3)∫sin^2 θdθ ......

$${let}\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}={t}\:\:\:\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right){dx}={dt} \\ $$$$\Rightarrow\:\:{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:,\:\:\mathrm{cos}\:{x}=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${I}=\int\frac{\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)\left(\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)}{\left(\mathrm{5}+\frac{\mathrm{4}−\mathrm{4}{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$$\:\:{I}=\:\mathrm{2}\int\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(\mathrm{9}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$${now}\:\:\:{let}\:\:\:{t}=\mathrm{3tan}\:\theta \\ $$$${dt}=\mathrm{3sec}\:^{\mathrm{2}} \theta{d}\theta \\ $$$${I}=\mathrm{2}\int\frac{\mathrm{1}−\mathrm{9tan}\:^{\mathrm{2}} \theta}{\mathrm{81sec}\:^{\mathrm{4}} \theta}\left(\mathrm{3sec}\:^{\mathrm{2}} \theta{d}\theta\right) \\ $$$${say}\:\:\:\mathrm{tan}\:\theta={z} \\ $$$${I}=\frac{\mathrm{2}}{\mathrm{27}}\int\mathrm{cos}\:^{\mathrm{2}} \theta{d}\theta−\frac{\mathrm{1}}{\mathrm{3}}\int\mathrm{sin}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\:\:...... \\ $$

Commented by jagoll last updated on 04/Apr/20

weierstrass substitution

$$\mathrm{weierstrass}\:\mathrm{substitution} \\ $$

Commented by ajfour last updated on 04/Apr/20

is this the name to the method?

$${is}\:{this}\:{the}\:{name}\:{to}\:{the}\:{method}? \\ $$

Commented by jagoll last updated on 04/Apr/20

yes sir

$$\mathrm{yes}\:\mathrm{sir} \\ $$

Commented by john santu last updated on 04/Apr/20

yes this method weierstrass substitution

$$\mathrm{yes}\:\mathrm{this}\:\mathrm{method}\:\mathrm{weierstrass}\: \\ $$$$\mathrm{substitution} \\ $$

Commented by ajfour last updated on 04/Apr/20

alright, i couldn′t go along any other line.

$${alright},\:{i}\:{couldn}'{t}\:{go}\:{along}\:{any} \\ $$$${other}\:{line}. \\ $$

Answered by TANMAY PANACEA. last updated on 04/Apr/20

t=5+4cosx→cosx=((t−5)/4) (1/4)∫((4cosx+5−5)/((5+4cosx)^2 ))dx (1/4)∫(dx/(5+4cosx))−(5/4)∫(dx/((5+4cosx)^2 ))★ let I_1 =∫(dx/(5+4cosx)) and I_2 =∫(dx/((5+4cosx)^2 )) so I=(I_1 /4)−((5I_2 )/4).......eqn (1) p=((sinx)/(5+4cosx)) (dp/dx)=(((5+4cosx)cosx−sinx(−4sinx))/((5+4cosx)^2 )) (dp/dx)=((5cosx+4)/((5+4cosx)^2 ))=((((5(t−5))/4)+4)/t^2 )=((5t−9)/(4t^2 ))=(5/(4t))−(9/(4t^2 )) ((sinx)/(5+4cosx))=(5/4)∫(dx/(5+cosx))−(9/4)∫(dx/((5+4cosx)^2 )) now look ((sinx)/(5+4cosx))=((5I_1 )/4)−((9I_2 )/4)....eqn(2) [5I_1 −4(((sinx)/(5+cosx)))]×(1/9)=I_2 ■ look if we find the value of I_1 =∫(dx/(5+4cosx)) then from eqn(2) we get value of I_2 finaly we get I=(I_1 /4)−((5I_2 )/4)■ ∫(dx/(5+4cosx))=∫((sec^2 (x/2))/(5+5tan^2 (x/2)+4−4tan^2 (x/2)))dx=∫((sec^2 (x/2))/(tan^2 (x/2)+3^2 )) =2∫((d(tan(x/2)))/(3^2 +tan^2 (x/2)))dx=2×(1/3)tan^(−1) (((tan(x/2))/3))+c_1 = I_1 =(2/3)tan^(−1) (((tan(x/2))/3)) I_2 =(1/9)[5I_1 −((4sinx)/(5+4cosx))] I_2 =(1/9)[((10)/3)tan^(−1) (((tan(x/2))/3))−((4sinx)/(5+4cosx))]^ finally I=(I_1 /4)−((5I_2 )/4)=(2/(12))tan^(−1) (((tan(x/2))/3))−(5/4)×(1/9)[((10)/3)tan^(−1) (((tan(x/2))/3))−((4sinx)/(5+4cosx))] I=((2/(12))−((50)/(108)))tan^(−1) (((tan(x/2))/3))+(5/(36))(((4sinx)/(5+4cosx)))+C

$${t}=\mathrm{5}+\mathrm{4}{cosx}\rightarrow{cosx}=\frac{{t}−\mathrm{5}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{4}{cosx}+\mathrm{5}−\mathrm{5}}{\left(\mathrm{5}+\mathrm{4}{cosx}\right)^{\mathrm{2}} }{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{\mathrm{5}+\mathrm{4}{cosx}}−\frac{\mathrm{5}}{\mathrm{4}}\int\frac{{dx}}{\left(\mathrm{5}+\mathrm{4}{cosx}\right)^{\mathrm{2}} }\bigstar\: \\ $$$$ \\ $$$${let}\:{I}_{\mathrm{1}} =\int\frac{{dx}}{\mathrm{5}+\mathrm{4}{cosx}}\:\:{and}\:{I}_{\mathrm{2}} =\int\frac{{dx}}{\left(\mathrm{5}+\mathrm{4}{cosx}\right)^{\mathrm{2}} } \\ $$$${so}\:{I}=\frac{{I}_{\mathrm{1}} }{\mathrm{4}}−\frac{\mathrm{5}{I}_{\mathrm{2}} }{\mathrm{4}}.......{eqn}\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$${p}=\frac{{sinx}}{\mathrm{5}+\mathrm{4}{cosx}} \\ $$$$\frac{{dp}}{{dx}}=\frac{\left(\mathrm{5}+\mathrm{4}{cosx}\right){cosx}−{sinx}\left(−\mathrm{4}{sinx}\right)}{\left(\mathrm{5}+\mathrm{4}{cosx}\right)^{\mathrm{2}} } \\ $$$$\frac{{dp}}{{dx}}=\frac{\mathrm{5}{cosx}+\mathrm{4}}{\left(\mathrm{5}+\mathrm{4}{cosx}\right)^{\mathrm{2}} }=\frac{\frac{\mathrm{5}\left({t}−\mathrm{5}\right)}{\mathrm{4}}+\mathrm{4}}{{t}^{\mathrm{2}} }=\frac{\mathrm{5}{t}−\mathrm{9}}{\mathrm{4}{t}^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{4}{t}}−\frac{\mathrm{9}}{\mathrm{4}{t}^{\mathrm{2}} } \\ $$$$\frac{{sinx}}{\mathrm{5}+\mathrm{4}{cosx}}=\frac{\mathrm{5}}{\mathrm{4}}\int\frac{{dx}}{\mathrm{5}+{cosx}}−\frac{\mathrm{9}}{\mathrm{4}}\int\frac{{dx}}{\left(\mathrm{5}+\mathrm{4}{cosx}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${now}\:{look} \\ $$$$\frac{{sinx}}{\mathrm{5}+\mathrm{4}{cosx}}=\frac{\mathrm{5}{I}_{\mathrm{1}} }{\mathrm{4}}−\frac{\mathrm{9}{I}_{\mathrm{2}} }{\mathrm{4}}....{eqn}\left(\mathrm{2}\right) \\ $$$$\left[\mathrm{5}{I}_{\mathrm{1}} −\mathrm{4}\left(\frac{{sinx}}{\mathrm{5}+{cosx}}\right)\right]×\frac{\mathrm{1}}{\mathrm{9}}={I}_{\mathrm{2}} \\ $$$$ \\ $$$$\blacksquare\:{look}\:{if}\:{we}\:{find}\:{the}\:{value}\:{of}\:{I}_{\mathrm{1}} =\int\frac{{dx}}{\mathrm{5}+\mathrm{4}{cosx}} \\ $$$${then}\:{from}\:{eqn}\left(\mathrm{2}\right)\:{we}\:{get}\:{value}\:{of}\:{I}_{\mathrm{2}} \\ $$$${finaly}\:{we}\:{get}\:{I}=\frac{{I}_{\mathrm{1}} }{\mathrm{4}}−\frac{\mathrm{5}{I}_{\mathrm{2}} }{\mathrm{4}}\blacksquare \\ $$$$\int\frac{{dx}}{\mathrm{5}+\mathrm{4}{cosx}}=\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{5}+\mathrm{5}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{4}−\mathrm{4}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx}=\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{3}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int\frac{{d}\left({tan}\frac{{x}}{\mathrm{2}}\right)}{\mathrm{3}^{\mathrm{2}} +{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx}=\mathrm{2}×\frac{\mathrm{1}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{3}}\right)+{c}_{\mathrm{1}} \:\:= \\ $$$$\boldsymbol{{I}}_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{3}}\right) \\ $$$$\boldsymbol{{I}}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{9}}\left[\mathrm{5}{I}_{\mathrm{1}} −\frac{\mathrm{4}{sinx}}{\mathrm{5}+\mathrm{4}{cosx}}\right] \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{9}}\left[\frac{\mathrm{10}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{3}}\right)−\frac{\mathrm{4}{sinx}}{\mathrm{5}+\mathrm{4}{cosx}}\overset{} {\right]} \\ $$$${finally} \\ $$$${I}=\frac{{I}_{\mathrm{1}} }{\mathrm{4}}−\frac{\mathrm{5}{I}_{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{2}}{\mathrm{12}}{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{3}}\right)−\frac{\mathrm{5}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{9}}\left[\frac{\mathrm{10}}{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{3}}\right)−\frac{\mathrm{4}{sinx}}{\mathrm{5}+\mathrm{4}{cosx}}\right] \\ $$$${I}=\left(\frac{\mathrm{2}}{\mathrm{12}}−\frac{\mathrm{50}}{\mathrm{108}}\right){tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{3}}\right)+\frac{\mathrm{5}}{\mathrm{36}}\left(\frac{\mathrm{4}{sinx}}{\mathrm{5}+\mathrm{4}{cosx}}\right)+{C} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by john santu last updated on 04/Apr/20

waw....amazing sir

$$\mathrm{waw}....\mathrm{amazing}\:\mathrm{sir} \\ $$

Commented by TANMAY PANACEA. last updated on 04/Apr/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by MJS last updated on 04/Apr/20

Weierstrass is the fastest ∫((cos x)/((5+4cos x)^2 ))dx= [t=tan (x/2) → dx=(2/(t^2 +1))dt] =−2∫((t^2 −1)/((t^2 +9)^2 ))dt= =20∫(dt/((t^2 +9)^2 ))−2∫(dt/(t^2 +9))= =((10t)/(9(t^2 +9)))−(8/(27))arctan (t/3) = =((5sin x)/(9(5+4cos x)))−(8/(27))arctan ((tan (x/2))/3) +C

$$\mathrm{Weierstrass}\:\mathrm{is}\:\mathrm{the}\:\mathrm{fastest} \\ $$$$\int\frac{\mathrm{cos}\:{x}}{\left(\mathrm{5}+\mathrm{4cos}\:{x}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\right] \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }{dt}= \\ $$$$=\mathrm{20}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} }−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{9}}= \\ $$$$=\frac{\mathrm{10}{t}}{\mathrm{9}\left({t}^{\mathrm{2}} +\mathrm{9}\right)}−\frac{\mathrm{8}}{\mathrm{27}}\mathrm{arctan}\:\frac{{t}}{\mathrm{3}}\:= \\ $$$$=\frac{\mathrm{5sin}\:{x}}{\mathrm{9}\left(\mathrm{5}+\mathrm{4cos}\:{x}\right)}−\frac{\mathrm{8}}{\mathrm{27}}\mathrm{arctan}\:\frac{\mathrm{tan}\:\frac{{x}}{\mathrm{2}}}{\mathrm{3}}\:+{C} \\ $$

Commented by jagoll last updated on 04/Apr/20

great sir. i like this method

$$\mathrm{great}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{like}\:\mathrm{this}\:\mathrm{method} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com